Содержание
Оборудование: источник электропитания для практикума ИЭПП-1, набор конденсаторов, комплект электроизмерительных приборов «Учебный-2», соединительные проводники.
Задание. Рассчитайте сопротивление конденсатора электроемкостью 6 мкФ в цепи переменного тока с частотой 50 Гц. Выполните измерение силы тока через конденсатор при включении в цепь с переменным напряжением 12 В.
Указание. Два проводника, разделенные слоем диэлектрика, обладают электроемкостью С. При подаче переменного напряжения между такими проводниками не происходит перенос электрических зарядов сквозь диэлектрик, но периодически повторяющиеся процессы зарядки и разрядки конденсатора приводят к возникновению переменного тока в проводах, ведущих к обкладкам конденсатора. Действующее значение силы тока  в проводах, ведущих к конденсатору, определяется значением его электроемкости С, частотой
в проводах, ведущих к конденсатору, определяется значением его электроемкости С, частотой  вынужденных колебаний силы тока в цепи и действующим значением напряжения
вынужденных колебаний силы тока в цепи и действующим значением напряжения  на обкладках:
на обкладках:

Таким образом, конденсатор в цепи переменного тока эквивалентен элементу цепи с электрическим сопротивлением  равным:
равным:

Возможный вариант выполнения работы
1. Вычислите емкостное сопротивление  этого конденсатора электроемкостью 6 мкФ на частоте 50 Гц.
этого конденсатора электроемкостью 6 мкФ на частоте 50 Гц.
2. Рассчитайте действующее значение силы тока через конденсатор при подаче на его обкладки переменного напряжения 12 В.
3. Выполните измерение силы тока через конденсатор при напряжении 12 В между его обкладками. Сравните результаты расчета и измерений.
Исследуйте зависимость действующего значения силы тока через конденсатор от действующего значения напряжения, постройте график. Рассчитайте значения силы тока в цепи при последовательном и параллельном включении конденсаторов с электроемкостью 6 и 4 мкФ. Результаты расчета проверьте экспериментально.
1. Объясните, почему через конденсатор не проходит постоянный ток, а переменный ток проходит.
2. Как изменится емкостное сопротивление конденсатора при увеличении частоты переменного тока в 2 раза?
Электросопротивление — это параметр в электротехнике, характеризующий возможность вещества препятствовать прохождению электричества. В зависимости от качеств материала, электросопротивляемость может уменьшаться до крайне маленьких величин (микромилиОмы — у проводников, металлов) или повышаться до огромных значений (ГигаОмы — изоляторов, диэлектриков). Величина противоположная сопротивлению — проводимость.
Что такое
Цепь, по которой протекает непостоянный ток, обладает полным сопротивлением. Вычисляется оно по сумме активного и реактивного сопротивлений, возведенных в квадрат.

Графическое изображение этой формулы представляет собой треугольник. Его катеты представлены активным и реактивным сопротивлениями, а гипотенуза полным электросопротивлением.

Емкостное электросопротивление (Xc) является одним из видов реактивного сопротивления. Этот показатель характеризует противодействие электроемкости в цепи электротоку с переменными параметрами. Преобразование электроэнергии в тепловую в момент протекания электричества сквозь емкость не возникает (свойство реактивного сопротивления). Вместо этого осуществляется передача энергии электрического тока электрическому полю и обратно. Потерь энергии при таком обмене не происходит.
Емкостное сопротивление конденсатора можно сравнить с кастрюлей, наполняемой жидкостью, при полном заполнении ее объема она переворачивается, выливая содержимое, а затем наполняется заново. После достижения максимального заряда конденсатора происходит разрядка, затем он заряжается вновь.
Дополнительная информация: Конденсатор цепи способен накопить лишь ограниченную величину заряда до перемены полярности напряжения. По данной причине непостоянный ток не падает до нуля, важное отличие от постоянного электричества. Низкие значения частоты тока соответствуют низким показателям заряда, накопленного конденсатором, низким значениям противодействия электричеству, что придает реактивные свойства.
По сути, Xc — это противостояние электродвижущей силы конденсатора, уровню его заряда.
От чего зависит сопротивление конденсаторов цепей переменного тока
Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.

Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.
При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.

Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.
При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.
Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку. Его электросопротивляемость является безваттной, реактивной.
Причины ёмкостного сопротивления
Причиной возникновения сопротивления емкостного считается уровень напряжения, возникающий на конденсаторе в процессе его заряда. Вектор его действия встречен вектору напряжения источника электричества, потому создает помеху воспроизведению электротока этим источником.
Как рассчитать Xc
Сила тока цепи с постоянными показателями напряжения в момент работы электроконденсатора равно 0. Ее значения в цепи с переменным напряжением после подключения конденсатора I ? 0. В итоге, цепочке с непостоянным напряжением конденсатор придает Xc меньшее, чем цепочке с неизменным показателем напряжения.


Получается, что изменения напряжения отличаются по фазе от изменений тока на π/2.
По закону, сформулированному Омом, показатели силы электротока находятся в прямой пропорциональной зависимости от величины напряжения цепи. Формула вычисления наибольших величин напряженности и силы тока:


f — показатель частоты непостоянного тока, измеряется в герцах;
ω — показатель угловой частоты тока;
С — размер конденсатора в фарадах.
Важно! Xc не выступает параметром проводника, оно находится в зависимости от такой характеристики электроцепи, как частота электротока.
Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается).
Представим, к цепи подключен конденсатор, емкостью 1 мкФ. Необходимо вычислить, уровень емкостного сопротивления при величине частоты 50 Гц и как изменится емкостное сопротивление цепи переменного тока при частоте 1 кГц. Амплитуда напряжения, подведенного к конденсатору, составляет 50 В.
После введения данных в формулу, определяющую Xc, и получаются значения:


Емкостное сопротивление приравнивается к соотношению отклонений колебаний напряжения зажимов электрической цепочки с емкостными параметрами (с небольшими индуктивным и активным сопротивлениями) к колебаниям электротока цепочки. Она равнозначна электроконденсатору.
В чем измеряется емкостное электросопротивление
R представлено отношением напряжения к силе тока замкнутой электрической цепи, по закону Ома. Единицы измерения — Ом. Xc, как его разновидность, тоже измеряется в Омах.
Конденсаторы применяются при изготовлении фильтров. При параллельном присоединении к цепи, он способен задерживать высокие частоты, при последовательном удаляет низкие. Также они используются с целью отсечения переменной части от постоянной. Он незаменим в радиотехнике, при производстве датчиков приближения, для контроля процессов производства. Технологии, обладающие выше описанными свойствами, используются во всех областях промышленности.
Емкость конденсатора при повышении частоты уменьшается, так как уменьшается диэлектрическая проницаемость диэлектрика, обусловленная ослаблением релаксационных видов поляризации.
Если же в диэлектрике имеет место только электронная и ионная поляризация, то диэлектрическая проницаемость в широком диапазоне частот не должна зависеть от частоты, а следовательно не должна изменяться и емкость. Но и в этом случае емкость может изменяться за счет влияния конструктивных элементов конденсатора: его индуктивности и сопротивления обкладок и выводов.
Наличие индуктивности в конденсаторе дает увеличение его действующей емкости с ростом частоты (рис. 30), так как ток будет возрастать за счет компенсации реактивного емкостного сопротивления индуктивным сопротивлением.
 Приравняем значения полных сопротивлений:
Приравняем значения полных сопротивлений:
конденсатора с индуктивностью, L и емкостью 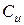
эквивалентного ему конденсатора с действующей емкостью  , без индуктивности.
, без индуктивности.
Пренебрегая наличием активного сопротивления можно написать:
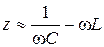 [84]
[84]
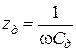 [85]
[85]
 [86]
[86]
 [87]
[87]
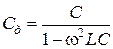 [88]
[88]
Зависимость  от частоты увеличивается как при увеличении индуктивности L так и при увеличении емкости при заданной индуктивности.
от частоты увеличивается как при увеличении индуктивности L так и при увеличении емкости при заданной индуктивности.
Наличие активного сопротивления r, включенного последовательно с емкостью С должно ограничивать ток, протекающий через конденсатор, причем этот эффект должен быть заметнее при увеличении частоты, так как с увеличением частоты падает емкостное реактивное сопротивление и влияние активного сопротивления на величину тока возрастает (рис. 31).
Величину  можно вычислить по формуле:
можно вычислить по формуле:

 [89]
[89]
Увеличение емкости С при заданном r усиливает частотную зависимость.
В обычных конденсаторах сопротивление обкладок и выводов, определяющее величину r, мало, а поэтому снижение емкости C с увеличением частоты f можно заметить лишь в области радиочастот, даже при больших емкостях.
Выражения [88] и [89] являются приближенными, хотя и правильно характеризуют качественный характер частотной зависимости емкости.
Как частотная зависимость диэлектрической проницаемости, так и влияние активного сопротивления вызывают уменьшение емкости от частоты; увеличение емкости может быть обусловлено только влиянием индуктивности.
Как для полярных, так и для неполярных диэлектриков величина диэлектрической проницаемости не зависит от напряженности, а поэтому для большинства типов конденсаторов емкость не должна зависеть от величины приложенного напряжения.
Небольшое увеличение емкости при увеличении напряжения выше напряжения ионизации может наблюдаться для конденсаторов, диэлектрик которого содержит значительное число воздушных включений.
В сегнетокерамических конденсаторах диэлектрик обладает спонтанной поляризацией, для которой характерна зависимость диэлектрической проницаемости от напряжения. Для них емкость сильно зависит от напряжения, что используется для изготовления нелинейных конденсаторов – «варикондов».
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10099 –  | 7532 –
| 7532 –  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
