Вектор напряженности электрического поля созданного двумя зарядами

Задание 13. Какое направление (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) имеет вектор напряжённости электрического поля, созданного двумя равными положительными зарядами в точке О, равноудалённой от зарядов (см. рисунок)? Ответ запишите словом (словами).

Вектор напряженности электрического поля исходит из положительного заряда и входит в отрицательный заряд. Величина вектора напряженности пропорциональна заряду и обратно пропорциональна квадрату расстояния от заряда. В точке О величины векторов напряженности, создаваемые зарядами +q и +q будут равны, а результирующий вектор напряженности будет направлен вправо как это показано на рисунке ниже (синяя линия).

По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля.

Характеристика электрического поля

Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле:

E → = F → q , где F → – сила, действующая со стороны поля на неподвижный (пробный) заряд q . Его значение должно быть настолько мало, чтобы отсутствовала возможность искажать поле, напряженность которого с его помощью и измеряют. По уравнению видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный пробный заряд.

У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным.

Силовые линии

Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий.

Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.

Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться.

Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:

E → = ∑ i = 1 n E → i .

Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле:

Интегрирование E → = ∫ d E → проводится по области распределения зарядов. Если их распределение идет по линии ( τ = d q d l – линейная плотность распределения заряда), то интегрирование E → = ∫ d E → тоже. Когда распределение зарядов идет по поверхности и поверхностная плоскость обозначается как σ = d q d S , тогда интегрируют по поверхности.

Интегрирование по объему выполняется, если имеется объемное распределение заряда:

ρ = d q d V , где ρ – объемная плотность распределения заряда.

Что называется напряженностью электрического поля

Напряженность поля в диэлектрике равняется векторной сумме напряженностей полей, которые создают свободные E 0 → и связанные E p → заряды:

Зачастую бывают случаи, когда диэлектрик изотропный. Тогда запись напряженности поля имеет вид:

E → = E 0 → ε , где ε обозначает относительную диэлектрическую проницаемость среды в рассматриваемой точке поля.

Отсюда следует, что по выражению E → = E 0 → ε имеется однородный изотропный диэлектрик с напряженностью электрического поля в ε меньше, чем в вакууме.

Напряженность электростатического поля системы точечных зарядов равняется:

E → = 1 4 π ε 0 ∑ i = 1 n q i ε r i 3 r i → .

В системе СГС напряженность поля точечного заряда в вакууме:

Дан равномерно распределенный заряд по четверти окружности радиуса R с линейной плотностью τ . Необходимо найти напряженность поля в точке А , являющейся центром окружности.

Решение

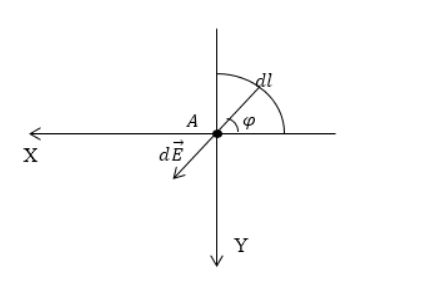
Произведем выделение на заряженной части окружности элементарного участка d l , который будет создавать элемент поля в точке А . Следует записать выражение для напряженности, то есть для d E → . Тогда формула примет вид:

d E → = d q R 3 R → R .

Проекция вектора d E → на ось О х составит:

d E x = d E cos φ = d q cos φ R 2 .

Произведем выражение d q через линейную плотность заряда τ :

d q = τ d l = τ · 2 πRdR .

Необходимо использовать d q = τ d l = τ · 2 πRdR для преобразования d E x = d E cos φ = d q cos φ R 2 :

d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,

где 2 π d R = d φ .

Далее перейдем к нахождению полной проекции E x при помощи интегрирования d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,

по d φ с изменением угла 0 ≤ φ ≤ 2 π .

E x = ∫ 0 2 π τ cos φ d φ R = τ R ∫ 0 2 π cos φ d φ = τ R sin φ 0 2 π = τ R .

Перейдем к проекции вектора напряженности на О у :

d E y = d E sin φ = τ R sin φ d φ .

Следует проинтегрировать с изменяющимся углом π 2 ≤ φ ≤ 0 :

E y ∫ π 2 0 τ R sin φ d φ = τ R ∫ π 2 0 sin φ d φ = – τ R cos φ π 2 0 = – τ R .

Произведем нахождение модуля вектора напряженности в точке А , применив теорему Пифагора:

E = E x 2 + E y 2 = τ R 2 + – τ R 2 = τ R 2 .

Ответ: E = τ R 2 .

Найти напряженность электростатического поля равномерно заряженной полусферы с радиусом R . Поверхностная плотность заряда равняется σ .

Решение

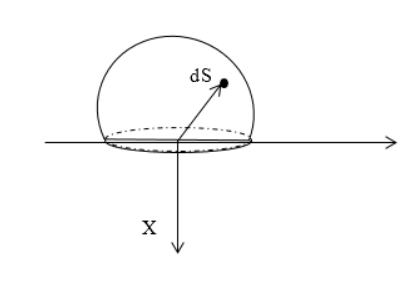
Следует выделить на поверхности заряженной сферы элементарный заряд d q , располагаемый на элементе площади d S . Запись, используя сферические координаты d S , равняется:

d S = R 2 sin θ d θ d φ ,

при 0 ≤ φ ≤ 2 π , 0 ≤ θ ≤ π 2 .

Элементарная напряженность поля точечного заряда в системе С И :

d E → = d q 4 π ε 0 R 3 R → R .

Необходимо спроецировать вектор напряженности на О х :

d E x = d q cos θ 4 π ε 0 R 2 .

Произведем выражение заряда через поверхностную плотность заряда:

Подставим d q = σ d S в d E x = d q cos θ 4 π ε 0 R 2 , используя d S = R 2 sin θ d θ d φ , проинтегрируем и запишем:

E x = σ R 2 4 π ε 0 R 2 ∫ 0 2 π d φ ∫ 0 π 2 cos θ sin θ d θ = σ 4 π ε 0 2 π · 1 2 = σ 4 ε 0 .

Отсюда следует, что E = E x .

Ответ: напряженность полусферы в центре равняется E = σ 4 ε 0 .

ЭЛЕКТРИЧЕСКИЙ ЗАРЯД. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ.

Электрический заряд q – физическая величина, определяющая интенсивность электромагнитного взаимодействия.

Атомы состоят из ядер и электронов. В состав ядра входят положительно заряженные протоны и не имеющие заряда нейтроны. Электроны несут отрицательный заряд. Количество электронов в атоме равно числу протонов в ядре, поэтому в целом атом нейтрален.

Заряд любого тела: q = ±Ne , где е = 1,6*10 -19 Кл – элементарный или минимально возможный заряд (заряд электрона), N – число избыточных или недостающих электронов. В замкнутой системе алгебраическая сумма зарядов остается постоянной:

Точечный электрический заряд – заряженное тело, размеры которого во много раз меньше расстояния до другого наэлектризованного тела, взаимодействующего с ним.

Два неподвижных точечных электрических заряда в вакууме взаимодействуют с силами, направленными по прямой, соединяющей эти заряды; модули этих сил прямо пропорциональны произведению зарядов и обратно пропорциональны квадрату расстояния между ними:

где – электрическая постоянная.

где ₁₂ – сила, действующая со стороны второго заряда на первый, а ₂₁ – со стороны первого на второй.

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. НАПРЯЖЕННОСТЬ

Факт взаимодействия электрических зарядов на расстоянии можно объяснить наличием вокруг них электрического поля – материального объекта, непрерывного в пространстве и способного действовать на другие заряды.

Поле неподвижных электрических зарядов называют электростатическим.

Характеристикой поля является его напряженность.

Напряженность электрического поля в данной точке – это вектор, модуль которого равен отношению силы, действующей на точечный положительный заряд, к величине этого заряда, а направление совпадает с направлением силы.

Напряженность поля точечного заряда Q на расстоянии r от него равна

Принцип суперпозиции полей

Напряженность поля системы зарядов равна векторной сумме напряженностей полей каждого из зарядов системы:

Диэлектрическая проницаемость среды равна отношению напряженностей поля в вакууме и в веществе:

Она показывает во сколько раз вещество ослабляет поле. Закон Кулона для двух точечных зарядов q и Q , расположенных на расстоянии r в среде c диэлектрической проницаемостью :

Напряженность поля на расстоянии r от заряда Q равна

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРО-СТАТИЧЕСКОМ ПОЛЕ

Между двумя большими пластинами, заряженными противоположными знаками и расположенными параллельно, поместим точечный заряд q .

Так как электрическое поле между пластинами с напряженностью однородное, то на заряд во всех точках действует сила F = qE , которая при перемещении заряда на расстояние вдоль совершает работу

Эта работа не зависит от формы траектории, то есть при перемещении заряда q вдоль произвольной линии L работа будет такой же.

Работа электростатического поля по перемещению заряда не зависит от формы траектории, а определяется исключительно начальным и конечным состояниями системы. Она, как и в случае с полем сил тяжести, равна изменению потенциальной энергии, взятому с противоположным знаком:

Из сравнения с предыдущей формулой видно, что потенциальная энергия заряда в однородном электростатическом поле равна:

Потенциальная энергия зависит от выбора нулевого уровня и поэтому сама по себе не имеет глубокого смысла.

ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И НАПРЯЖЕНИЕ

Потенциальным называется поле, работа которого при переходе из одной точки поля в другую не зависит от формы траектории. Потенциальными являются поле силы тяжести и электростатическое поле.

Работа, совершаемая потенциальным полем, равна изменению потенциальной энергии системы, взятой с противоположным знаком:

Потенциал – отношение потенциальной энергии заряда в поле к величине этого заряда:

Потенциал однородного поля равен

где d – расстояние, отсчитываемое от некоторого нулевого уровня.

Потенциальная энергия взаимодействия заряда q с полем равна .

Поэтому работа поля по перемещению заряда из точки с потенциалом φ₁ в точку с потенциалом φ₂ составляет:

Величина называется разностью потенциалов или напряжением.

Напряжение или разность потенциалов между двумя точками – это отношение работы электрического поля по перемещению заряда из начальной точки в конечную к величине этого заряда:

НАПРЯЖЕННОСТЬ ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ

При перемещении заряда q вдоль силовой линии электрического поля напряженностью на расстояние Δ d поле совершает работу

Так как по определению, то получаем:

Отсюда и напряженность электрического поля равна

Итак, напряженность электрического поля равна изменению потенциала при перемещении вдоль силовой линии на единицу длины.

Если положительный заряд перемещается в направлении силовой линии, то направление действия силы совпадает с направлением перемещения, и работа поля положительна:

Тогда , то есть напряженность направлена в сторону убывания потенциала.

Напряженность измеряют в вольтах на метр:

Напряженность поля равна 1 В/м, если напряжение между двумя точками силовой линии, расположенными на расстоянии 1 м, равна 1 В.

Если независимым образом измерять заряд Q , сообщаемый телу, и его потенциал φ, то можно обнаружить, что они прямо пропорциональны друг другу:

Величина С характеризует способность проводника накапливать электрический заряд и называется электрической емкостью. Электроемкость проводника зависит от его размеров, формы, а также электрических свойств среды.

Электроёмкостъ двух проводников – отношение заряда одного из них к разности потенциалов между ними:

Емкость тела равно 1 Ф , если при сообщении ему заряда 1 Кл оно приобретает потенциал 1 В.

Конденсатор – два проводника, разделенные диэлектриком, служащие для накопления электрического заряда. Под зарядом конденсатора понимают модуль заряда одной из его пластин или обкладок.

Способность конденсатора накапливать заряд характеризуется электроемкостью, которая равна отношению заряда конденсатора к напряжению:

Емкость конденсатора равна 1 Ф, если при напряжении 1 В его заряд равен 1 Кл.

Емкость плоского конденсатора прямо пропорциональна площади пластин S , диэлектрической проницаемости среды , и обратно пропорциональна расстоянию между пластинами d:

ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА.

Точные эксперименты показывают, что W=CU 2 /2

Так как q = CU , то

Плотность энергии электрического поля

где V = Sd – объем, занимаемый полем внутри конденсатора. Учитывая, что емкость плоского конденсатора

а напряжение на его обкладках U=Ed

Пример. Электрон, двигаясь в электрическом поле из точки 1 через точку 2, увеличил свою скорость от 1000 до 3000 км/с. Определите разность потенциалов между точками 1 и 2.

Так как электрон увеличил свою скорость, то ускорение и сила Кулона сонаправлены со скоростью. Значит, электрон движется против силовых линий поля. Изменение кинетической энергии электрона равно работе поля :

Ответ: разность потенциалов равна – 22,7 В.