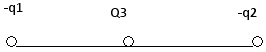ЛЕКЦИЯ 4. Электромагнитные волны (ЭМВ).
Электрическое поле, созданное неподвижными электрическими зарядами, с течением времени остается неизменным. Такое поле получило название потенциального электрического поля (электростатическое поле). Неизменным с течением времени остается и магнитное поле, образованное постоянным электрическим током. Эти поля существуют независимо друг от друга. Картина существенным образом изменяется, если электрическое поле создается движущимися электрическими зарядами. Согласно теории Максвелла, изменяющееся со временем электрическое поле создает изменяющееся со временем магнитное поле
и наоборот,изменяющееся со временем магнитное поле, являющееся по самой своей природе вихревым, создает вихревое электрическое поле (силовые линии, т. е. линии напряженности такого электрического поля, являются замкнутыми) (рис.1).
Рис. 1. Графическое представление взаимосвязи вихревых электрического и магнитного полей.
вектор напряженности электрического поля
– вектор индукции магнитного поля, связан с вектором напряженности магнитного поля соотношением ( – магнитная проницаемость среды).
Согласно Максвеллу, переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. электрическое и магнитное поле "сцеплены" и неразрывно связаны друг с другом и образуют единое электромагнитное поле.
Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение, так называемый, ток смещения. Током смещения объяснялось протекание переменного электрического тока через конденсатор между его обкладками, т. е. через те участки цепи, где отсутствуют проводники. Максвелл высказал предположение, что ток смещения, как и ток проводимости создает магнитное поле. Ток смещения по своей сути – это изменяющееся со временем электрическое поле, поэтому ток смещения существует и в вакууме. Введя понятие тока смещения, Максвелл по-новому подошел к рассмотрению замкнутых цепей переменного тока. Там, где на концах проводника обрывается ток проводимости, продолжается ток смещения и т. д. Следовательно, полный ток в цепи переменного тока может быть представлен суммой токов проводимости и токов смещения.
При неравномерном движении электрических зарядов, в частности, при их колебательном движении, а значит и при всяком переменном токе, электрическое и магнитное поле будут меняться с течением времени; эти изменения будут передаваться от одной точки пространства к другой, образуя, предсказанную Максвеллом, электромагнитную (ЭМ ) волну. В дальнейшем было показано, что скорость распространения электромагнитных волн (ЭМВ ) в вакууме имеет значение , совпадающее с экспериментально полученным значением скорости света. Обобщение экспериментальных данных (опыты Эрстеда, сила Ампера, закон Био-Савара-Лапласа, основной закон электромагнитной индукции) привело к заключению, что при распространении ЭМВ электрические и магнитные поля имеет взаимно перпендикулярную ориентацию. В направлении распространения ЭМ волну можно представить с помощью двух синусоид, лежащих во взаимно перпендикулярных плоскостях. Одна из них изображает колебания вектора напряженности электрического поля , а другая – вектора напряженности магнитного поля .
Оба вектора колеблются в одинаковой фазе, т.е. одновременно достигают максимальных и нулевых значений. Направление распространения ЭВ волны (направление вектора скорости ) определяется правилом правого винта (буравчика) (рис. 2). Рисунок хорошо иллюстрирует тот факт, что ЭМ волны являются поперечными, поскольку колебания векторов и происходят в плоскостях, перпендикулярных направлению распространения волны(ось OY ).
Рис.2. Графическое представление электромагнитной волны. Электромагнитная теория Максвелла была блестяще подтверждена опытами Герца по распространению ЭМВ.
Общие свойства ЭМВ.
1. ЭМВ поперечные. Векторы напряженностей электрического и магнитного полей взаимно перпендикулярны и образуют правовинтовую систему с направлением распространения волны.
2. Скорость распространения (фазовая) в непроводящей среде , где
3. в бегущей волне всегда колеблются в фазе и одновременно достигают максимальных (амплитудных ) и нулевых значений. В фиксированной точке пространства векторы изменяются со временем по гармоническому закону:
| | | следующая лекция ==> | |
| Колебания струны | | | Строение клетки прокариот |
Дата добавления: 2015-06-12 ; просмотров: 3527 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Разделы: Физика
Цель урока: дать понятие напряжённости электрического поля и ее определения в любой точке поля.
- формирование понятия напряжённости электрического поля; дать понятие о линиях напряжённости и графическое представление электрического поля;
- научить учащихся применять формулу E=kq/r 2 в решении несложных задач на расчёт напряжённости.
Электрическое поле – это особая форма материи, о существовании которой можно судить только по ее действию. Экспериментально доказано, что существуют два рода зарядов, вокруг которых существуют электрические поля, характеризующиеся силовыми линиями.
Графически изображая поле, следует помнить, что линии напряженности электрического поля:
- нигде не пересекаются друг с другом;
- имеют начало на положительном заряде (или в бесконечности) и конец на отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
- между зарядами нигде не прерываются.
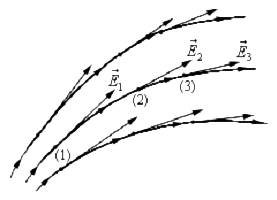
Рис.1
Силовые линии положительного заряда:
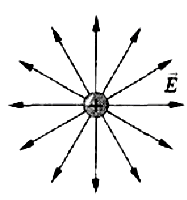
Рис.2
Силовые линии отрицательного заряда:
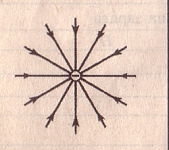
Рис.3
Силовые линии одноименных взаимодействующих зарядов:
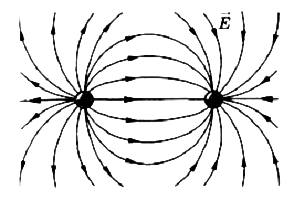
Рис.4
Силовые линии разноименных взаимодействующих зарядов:
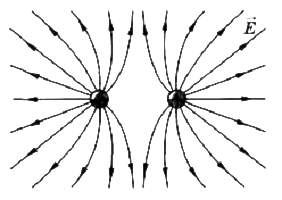
Рис.5
Силовой характеристикой электрического поля является напряженность, которая обозначается буквой Е и имеет единицы измерения 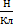 или
или  . Напряженность является векторной величиной, так как определяется отношением силы Кулона к величине единичного положительного заряда
. Напряженность является векторной величиной, так как определяется отношением силы Кулона к величине единичного положительного заряда
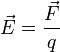
В результате преобразования формулы закона Кулона и формулы напряженности имеем зависимость напряженности поля от расстояния, на котором она определяется относительно данного заряда
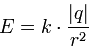
где: k – коэффициент пропорциональности, значение которого зависит от выбора единиц электрического заряда.
В системе СИ 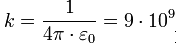 Н·м 2 /Кл 2 ,
Н·м 2 /Кл 2 ,
где ε 0 – электрическая постоянная, равная 8,85·10 -12 Кл 2 /Н·м 2 ;
q – электрический заряд (Кл);
r – расстояние от заряда до точки в которой определяется напряженность.
Направление вектора напряженности совпадает с направлением силы Кулона.
Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным. В ограниченной области пространства электрическое поле можно считать приблизительно однородным, если напряженность поля внутри этой области меняется незначительно.
Общая напряженность поля нескольких взаимодействующих зарядов будет равна геометрической сумме векторов напряженности, в чем и заключается принцип суперпозиции полей:
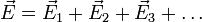
Рассмотрим несколько случаев определения напряженности.
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный положительный заряд между ними, тогда в данной точке будут действовать два вектора напряженности, направленные в одну сторону:
Е31 – напряженность точечного заряда 3 со стороны заряда 1;
Е32 – напряженность точечного заряда 3 со стороны заряда 2.
Согласно принципу суперпозиции полей общая напряженность поля в данной точке равна геометрической сумме векторов напряженности Е31 и Е32.
Напряженность в данной точке определяется по формуле:
где: r – расстояние между первым и вторым зарядом;
х – расстояние между первым и точечным зарядом.
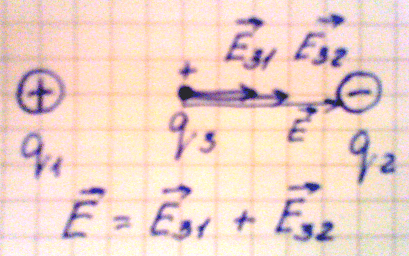
Рис.6
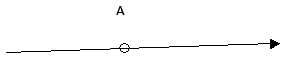
2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной на расстояние а от второго заряда. Если учесть, что поле первого заряда больше, чем поле второго заряда, то напряженность в данной точке поля равна геометрической разности напряженности Е31 и Е32.
Формула напряженности в данной точке равна:
Е = kq1/(r + a) 2 – kq2/a 2
Где: r – расстояние между взаимодействующими зарядами;
а – расстояние между вторым и точечным зарядом.
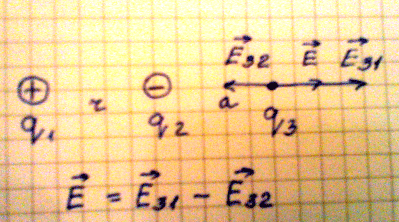
Рис.7
3. Рассмотрим пример, когда необходимо определить напряженность поля в некоторой удаленности и от первого и от второго заряда, в данном случае на расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные заряды отталкиваются , а разноименные притягиваются, имеем два вектора напряженности исходящие из одной точки, то для их сложения можно применить метод противоположному углу параллелограмма будет являться суммарным вектором напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:
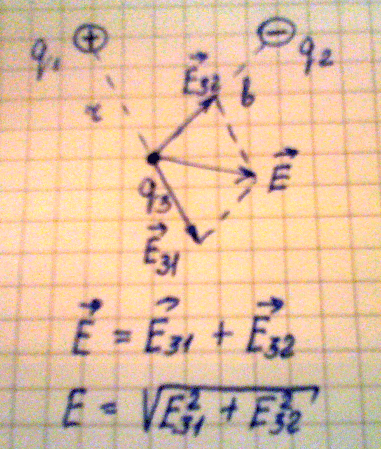
Рис.8
Исходя из данной работы, следует, что напряженность в любой точке поля можно определить, зная величины взаимодействующих зарядов, расстояние от каждого заряда до данной точки и электрическую постоянную.
4. Закрепление темы.
| фамилия |
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: электрическое поле – это ….
3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности. 
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
| фамилия |
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: напряженностью называется …
3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
1. Два заряда q1 = +3·10 -7 Кл и q2 = −2·10 -7 Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите напряженность поля в точке С, расположенной на линии, соединяющей заряды, на расстоянии 0,05 м вправо от заряда q2.
2. В некоторой точке поля на заряд 5·10 -9 Кл действует сила 3·10 -4 Н. Найти напряженность поля в этой точке и определите величину заряда, создающего поле, если точка удалена от него на 0,1 м.
Напряженность электрического поля измеряют с помощью пробного заряда Если величину пробного заряда уменьшить в n раз, то модуль напряженности измеряемого поля
2) увеличится в n раз
3) уменьшится в n раз
4) увеличится в раз
Сила, с которой электрическое поле действует на пробный электрический заряд пропорциональна величине этого заряда, поэтому величина напряженности электрического поля не зависит от величины пробного заряда
по этой формуле же увеличится в n раз
Читайте внимательнее. Сила, действующая на пробный заряд, пропорциональна его величине. Если бы напряженность зависела от величины заряда, то какой бы был прок в такой характеристике поля?
Для электрической напряженности также существует формула E=k*q/r^2. по ней напряженность и заряд прямопропорциональны. как быть?
Напряженность создает другой заряд, который не изменяется.
Металлическому полому телу, сечение которого представлено на рисунке, сообщен отрицательный заряд. Каково соотношение между потенциалами точек 1, 2 и 3, если тело помещено в однородное электростатическое поле?
1)
2)
3)
4)
Металл является проводником. Проводник, помещенный в электростатическое поле является эквипотенциальным телом, то есть все его точки находятся под одинаковым потенциалом. Действительно, если предположить обратное и допустить, что в проводнике есть точки с разными потенциалами, то между этими точками будет ненулевая разность потенциалов, а значит, эти точки проводника будут находиться под ненулевым электрическим напряжением, но тогда в проводнике должен течь ток, что противоречит исходному предположению о том, что все электростатично. Таким образом, при помещении проводника в электростатическое поле заряды на его поверхности всегда перераспределяются таким образом, чтобы потенциал всех точек был одинаковым. Более того, если в проводнике имеется полость, то все точки полости также имеют потенциал, совпадающий по величине с потенциалом проводника. Это явление называется экранировкой электростатического поля. Таким образом, верно утверждение 1.