Вещества с наибольшей теплопроводностью

Основные определения

Явление теплопроводности состоит в переносе теплоты структурными частицами вещества – молекулами, атомами, электронами – в процессе их теплового движения. В жидкостях и твердых телах- диэлектриках – перенос теплоты осуществляется путем непосредственной передачи теплового движения молекул и атомов соседним частицам вещества. В газообразных телах распространение теплоты теплопроводностью происходит вследствие обмена энергией при соударении молекул, имеющих различную скорость теплового движения. В металлах теплопроводность осуществляется главным образом вследствие движения свободных электронов.

В основной зеком теплопроводности входит ряд математических понятий, оп­ределения которых, целесообразно напомнить и пояснить.

Температурное поле — это со­вокупности значений температуры во всех точках тела в данный момент време­ни. Математически оно описывается ввиде t = f(x, y, z, τ). Различают стационарное температурное поле, когда температура во всех точках тела не зависит от времени (не изменяется с течением времени), и нестационарное температурное поле. Кроме то­го, если температура изменяется только по одной или двум пространственным координатам, то температурное поле на­зывают соответственно одно- или двух – мерным.

Изотермическая поверхность – это геометрическое место точек, температура в которых одинакова.

Градиент температуры — grad t есть вектор, направленный по нор­мали к изотермической поверхности и численно равный производной от тем­пературы по этому направлению.

Согласно основному закону тепло­проводности — закону Фурье (1822 г.), вектор плотности теплового потока, передаваемого теплопроводностью, пропорционален градиенту температуры:

где λ — коэффициент теплопро­водности вещества; его единица измерения Вт/(м·К).

Знак минус в уравнении (3) ука­зывает на то, что вектор q направлен противоположно вектору grad t, т.е. в сторону наибольшего уменьшения температуры.

Тепловой поток δQ через произволь­но ориентированную элементарную пло­щадку dF равен скалярному произведе­нию вектора q на вектор элементарной площадки dF, а полный тепловой поток Q через всю поверхность F определяется интегрированием этого произведения по поверхности F:

(4)

КОЭФФИЦИЕНТ ТЕПЛОПРОВОДНОСТИ

Коэффициент теплопроводности λ в законе Фурье (3) характеризует спо­собность данного вещества проводить теплоту. Значения коэффициентов тепло­проводности приводятся в справочниках по теплофизическим свойствам веществ. Численно коэффициент теплопроводности λ = q/grad t равен плотности теплового потока q при градиенте температуры grad t = 1 К/м. Наиболь­шей теплопроводностью обладает легкий газ — водород. При комнатных условиях коэффициент теплопроводности водорода λ = 0,2 Вт/(м·К). У более тяжелых газов теплопроводность меньше — у воз­духа λ = 0,025 Вт/(м·К), у диоксида уг­лерода λ = 0,02 Вт/(м·К).

Наибольшим коэффициентом теплопроводности обладают чистые серебро и медь: λ = 400 Вт/(м·К). Для углеродистых сталей λ = 50 Вт/(м·К). У жидкостей коэффициент теплопроводности, как правило, меньше 1 Вт/(м·К). Вода является одним из лучших жидких проводников теплоты, для нее λ = 0,6 Вт/(м·К).

Коэффициент теплопроводности неметаллических твердых материалов обычно ниже 10 Вт/(м·К).

Пористые материалы – пробка, различные волокнистые наполнители типа органической ваты – обладают наименьшими коэффициентами теплопроводности λ

Перенос теплоты теплопроводностью

Однородная плоская стенка.

Про­стейшей и очень распространенной за­дачей, решаемой теорией теплообмена, является определение плотности тепло­вого потока, передаваемого через плоскую стенку толщиной δ, на повер­хностях которой поддерживаются темпе­ратуры t_w1 и t_w2. (рис.2). Температура изменяется только по толщине пластины – по одной координате х. Такие за­дачи называются одномерными, решения их наиболее просты, и в данном курсе мы ограничимся рассмотрением только од­номерных задач.

Учитывая, что для од­номерного случая:

и используя основной закон теплопроводности (2), получаем дифференци­альное уравнение стационарной тепло­проводности для плоской стенки:

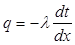(6)

В стационарных условиях, когда энергия не расходуется на нагрев, плот­ность теплового потока q неизменна по толщине стенки. В большинстве практи­ческих задач приближенно пред­полагается, что коэффициент тепло­проводности λ не зависит от температуры и одинаков по всей толщине стенки. Зна­чение λ находят в справочниках при температуре:

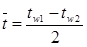, (6)

средней между температурами поверхно­стей стенки. (Погрешность расчетов при этом обычно меньше погрешности исход­ных данных и табличных величин, а при линейной зависимости коэффициента теплопроводности от температуры: λ = а+ bt точная расчетная формула для q не отличается от приближенной). При λ = const:

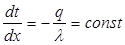(7)

т.е. зависимость температуры t от координаты х линейна (рис. 2).

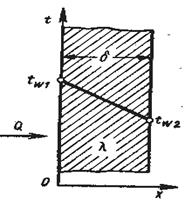
Рис.2. Стационарное распределение темпе­ратуры по толщине плоской стенки.

Разделив переменные в уравнении (7) и проинтегрировав по t от t_w1 до t_w2 и по х от 0 до δ:

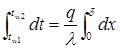, (8)

получим зависимость для расчета плот­ности теплового потока:

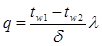, (9)

или мощность теплового потока (тепловой поток):

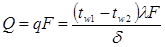(10)

Следовательно, количество теплоты, переданной через 1 м 2 стенки, прямо пропорционально коэффициенту теплопроводности λ и разности температур наружных поверхностей стенки (t_w1 – t_w2) и обратно пропорционально толщине стенки δ. Общее количество теплоты через стенку площадью F еще и пропорционально этой площади.

Полученная простейшая формула (10) имеет очень широкое распространение в тепло­вых расчетах. По этой формуле не только рассчитывают плотности теплового потока через плоские стенки, но и делают оценки для случаев более сложных, уп­рощенно заменяя в расчетах стенки сложной конфигурации на плоскую стенку. Иногда уже на основании оценки тот или иной вариант отвергается без дальней­ших затрат времени на его детальную проработку.

Но формуле (10) можно рассчитать коэффициент теплопроводности материа­ла, если экспериментально измерить тепловой поток и разность температур на поверхностях пластины (стенки) извест­ных размеров.

Температура тела в точке х определяется по формуле:

Отношение λF/δ называется тепло­вой проводимостью стенки, а обратная величина δ/λF тепловым или термическим сопротивлением стенки и обозначается R_λ. Пользуясь понятием термического сопро­тивления, формулу для расчета теплово­го потока можно представить в виде:

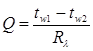. (11)

Зависимость (11) аналогична закону Ома в электротехни­ке (сила электрического тока равна раз­ности потенциалов, деленной на электри­ческое сопротивление проводника, по ко­торому течет ток).

Очень часто термическим сопротив­лением называют величину δ/λ, которая равна термическому сопротивлению плоской стенки площадью 1 м 2 .

Примеры расчетов.

Пример 1. Определить тепловой поток через бетонную стену здания толщиной 200 мм, высотой H = 2,5 м и длиной 2 м, если температуры на ее поверхностях: t_с1 = 20 0 С, t_с2 = – 10 0 С, а коэффициент теплопроводно­сти λ =1 Вт/(м·К):

= 750 Вт.

Пример 2. Определить коэффициент теплопроводности материала стенки толщиной 50 мм,если плотность теплового потока через нее q = 100 Вт/м 2 , а разность температур на поверхностях Δt = 20 0 С.

Вт/(м·К).

Многослойная стенка.

Формулой (10) можно воспользоваться и для расчета теплового потока через стенку, состоя­щую из нескольких (n) плотно прилегающих друг к другу слоев разнородных материа­лов (рис. 3), например, головку цилиндров, прокладку и блока цилиндров, выполненных из разных материалов, и т д.

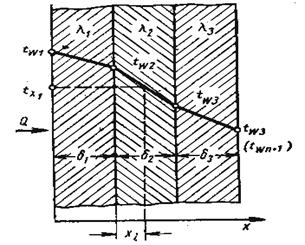
Рис.3. Распределение температуры по толщине многослойной плоской стенки.

Термическое сопротивление такой стенки равно сумме термических сопротивлений отдельных слоев:

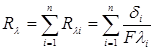(12)

В формулу (12) нужно подставить разность температур в тех точках (по­верхностях), между которыми «включе­ны» все суммируемые термические сопротивления, т.е. в данном случае: t_w1 и t_w(n+1):

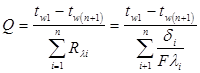, (13)

где i – номер слоя.

При стационарном режиме удельный тепловой поток через многослойную стенку постоянен и для всех слоев одинаков. Из (13) следует:

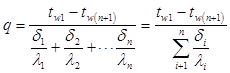. (14)

Из уравнения (14) следует, что общее термическое сопротивление многослойной стенки равно сумме сопротивлений каждого слоя.

Формулу (13) легко получить, записав разность температур по формуле (10) для каждого из п слоев многослой­ной стенки и сложив все п выражений с учетом того, что во всех слоях Q имеет одно и то же значение. При сложении все промежуточные температуры сократятся.

Распределение температуры в преде­лах каждого слоя — линейное, однако, в различных слоях крутизна температур­ной зависимости различна, поскольку со­гласно формуле (7) (dt/dx)_i = – q/λ_i. Плотность теплового потока, проходяще­го через все слон, в стационарном режи­ме одинакова, а коэффициент теплопро­водности слоев различен, следовательно, более резко температура меняется в сло­ях с меньшей теплопроводностью. Так, в примере на рис.4 наименьшей тепло­проводностью обладает материал второ­го слоя (например, прокладки), а наибольшей — третьего слоя.

Рассчитав тепловой поток через мно­гослойную стенку, можно определить па­дение температуры в каждом слое по соотношению (10) и найти температу­ры на границах всех слоев. Это очень важно при использовании в качестве теплоизоляторов материалов с ограничен­ной допустимой температурой.

Температура слоев определяется по следующей формуле:

Контактное термическое сопротивле­ние. При выводе формул для многослойной стенки предполагалось, что слои плотно прилегают друг к другу, и благодаря хорошему контакту соприкасающиеся поверхности разных слоев имеют одну и ту же температуру. Идеально плотный контакт между отдельными слоями многослойной стенки получается, если одни из слоев наносят на другой слой в жидком состоянии или в виде текучего раствора. Твердые тела касаются друг друга только вершинами профилей шеро­ховатостей (рис.4).

Площадь контакта вершин пренебрежимо мала, и весь тепловой по­ток идет через воздушный зазор (h). Это создает дополнительное (контактное) термическое сопротивление R_к. Термические контактные сопротивления, могут быть определены самостоятельно с использованием соответствующих эмпирических зависимостей или экспериментально. Например, термическое сопротивление зазора в 0,03 мм примерно эквивалентно термическому сопро­тивлению слоя стали толщиной около 30 мм.

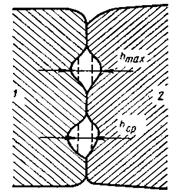
Рис.4. Изображение контактов двух шерохо­ватых поверхностей.

Методы снижения термического контактного сопротивления. Полное термическое сопротивление контакта определяется чистотой обработки, нагрузкой, теплопроводностью среды, коэффициентами теплопроводности материалов контактирующих деталей и другими факторами.

Наибольшую эффективность снижения термического сопротивления дает введение в контактную зону среды с теплопроводностью, близкой к теплопроводности металла.

Существуют следующие возможности заполнения контактной зоны веществами:

– использование прокладок из мягких металлов;

– введение в контактную зону порошкообразного вещества с хорошей тепловой проводимостью;

– введение в зону вязкого вещества с хорошей тепловой проводимостью;

– заполнение пространства между выступами шероховатостей жидким металлом.

Наилучшие результаты получены при заполнении контактной зоны расплавленным оловом. В этом случае термическое сопротивление контакта практически становится равным нулю.

Цилиндрическая стенка.

Очень часто теплоносители движутся по трубам (цилиндрам), и требуется рассчитать тепловой поток, передаваемый через цилиндрическую стенку трубы (цилиндра). Задача о передаче теплоты через цилиндрическую стенку (при известных и постоянных значениях температуры на внутренней и наружной поверхностях) также является одномерной, если ее рассматри­вать в цилиндрических координатах (рис.4).

Температура изменяется только вдоль радиуса, а по длине трубы l и по ее периметру остается неизменной.

В этом случае уравнение теплового потока имеет вид:

. (15)

Зависимость (15) показывает, что количество теплоты, переданной через стенку цилиндра, прямо пропорционально коэффициенту теплопроводности λ, длине трубы l и температурному напору (t_w1 – t_w2) и обратно пропорционально натуральному логарифму отношения внешнего диаметра цилиндра d₂ к его внутреннему диаметру d₁.

Рис. 4. Изменение температуры по толщине однослойной цилиндрической стенки.

При λ = const распределение темпера­туры порадиусу r однослойной цилиндрической стенки подчиняется ло­гарифмическому закону (рис. 4).

Пример . Во сколько раз уменьшаются тепловые потери через стенку здания, если между двумя слоями кирпичей толщиной по 250 мм установить прокладку пенопласта толщиной 50 мм. Коэффициенты теплопроводности соответственно равны: λ_кирп. = 0,5 Вт/(м·К); λ_пен.. = 0,05 Вт/(м·К).

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 10458 – | 7917 – или читать все.

Физика А.В. Перышкин

1. Как происходит передача энергии по металлической проволоке?

Если нагревать один конец проволоки, проволока будет постепенно нагреваться все дальше и дальше от места нагрева, поскольку частицы вещества постоянно взаимодействуют друг с другом и скорость движения соседних частиц будет увеличиваться с нагревом, хотя само вещество не перемещается, а только энергия передается по проволоке.

2. Объясните опыт (см. рис. 8), показывающий, что теплопроводность меди больше, чем теплопроводность стали.

В опыте, изображенном на рис. 8, гвоздики, прикрепленные воском к медной проволоке, раньше отрываются, чем отрываются гвоздики от стальной проволоки, значит по медной проволоке тепло передается быстрее, чем по стальной, что означает: теплопроводность меди выше теплопроводности стали.

3. Какие вещества имеют наибольшую и наименьшую теплопроводность? Где их применяют?

Самой низкой теплопроводностью обладает вакуум, что используется например в быту (термос), в науке и промышленности (при хранении сжиженных газов в сосудах Дьюара). Вообще вещества обладающие низкой теплопроводность используется в качестве теплоизоляторов, например воздух, как плохой теплопроводник используется для теплоизоляции домов, он содержится между стеклами окон и препятствует охлаждению домов зимой.
Металлы хорошо проводят тепло, особенно высокой теплопроводностью отличаются серебро и медь. Вещества хорошо проводящие тепло используются в качестве теплообменников, например для отвода тепла от двигателей автомашин.

4. Почему мех, пух, перья на теле животных и птиц, а также одежда человека защищают от холода?

Мех, пух, перья на теле животных и птиц, а также одежда человека тем теплее, чем более пушистые они, то есть в них больше воздуха, который имеет низкую теплопроводность, значит лучше сохраняют тепло.

Теплопроводность – способность материала передавать теплоту. Для количественного определения этой характеристики используется коэффициент теплопроводности , который равен количеству тепла, проходящему за 1 час через образец материала толщиной 1 м и площадью 1 м 2 при разности температур на противоположных поверхностях 1°С. Теплопроводность выражается в Вт/(м К) или Вт/(м градус Цельсия).
Теплопроводность зависит от средней плотности и химико-минерального состава материала, его структуры, пористости, влажности и средней температуры материала. Чем больше пористость (меньше средняя плотность), тем ниже теплопроводность материала. С увеличением влажности материала теплопроводность резко увеличивается, т.е. снижаются показатели теплоизоляционных свойств материала.

Теплопроводность некоторых материалов, Вт/(м*k)