Содержание
 Рис.3.16 |
Пусть по проводнику длиной l и сечением S течет ток I. В проводнике создается электрическое поле напряженности E, а j1 и j2 – потенциалы на концах проводника (рис.3.16). В случае однородного проводника величину j1 – j2 = U можно назвать падением напряжения на участке проводника. |
Закон Ома: сила тока, текущего по однородному участку проводника, прямо пропорциональна падению напряжения на проводнике:
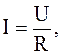(3.47)
где R – электрическое сопротивление проводника.
(3.47) – закон Ома в интегральной форме.
Размерность сопротивления в СИ: [R] = В/А = Ом.
Ом – сопротивление такого проводника, в котором при напряжении в 1 В течет ток 1А.
Сопротивление зависит от геометрических размеров и формы проводников, материала и температуры проводников. Для цилиндрического проводника
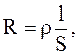(3.48)
где r – удельное сопротивление проводника.
Удельное сопротивление численно равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м 2 . Размерность удельного сопротивления в СИ: [r] = Ом×м.
Величина, обратная сопротивлению, называется проводимостью.
Величина, обратная удельному сопротивлению, называется удельной проводимостью:
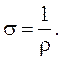(3.49)
Единица, обратная Ом, называется Сименсом [См].
Учитывая (3.46) – (3.49), а также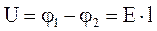 
, получим:
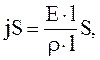
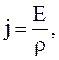
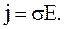(3.50)
(3.50) – закон Ома в дифференциальной форме.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Учись учиться, не учась! 10458 – 
| 7918 – 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Для того, чтобы перейти к интегральной форме записи закона Ома для участка проводника, на котором действуют две силы, введем понятие линии тока.
Линия тока – кривая, в каждой точке которой вектор плотности тока направлен по касательной к этой кривой. В этом случае вектор плотности находится из соотношения:
где τ ⃗ – единичный вектор касательной к линии тока.
Предположим, что удельное сопротивление (r) и напряженность поля движущих сил (E ⃗) на поперечном сечении проводника однородны, т.к. E ⃗ однородна, то j ⃗ так же однородная величина. Возьмем произвольное значение поперечного сечения цепи – S. Тогда:
, а значит 
Последнее равенство до множим на dl (элементарное перемещение вдоль вектора плотности тока):
где
- dφ – элементарный сброс потенциала электростатического поля,
- dε – элементарная работа сторонних сил по перемещению единичного положительного заряда (ЭДС).
Отсюда: 
Учитывая, что ρ/S dl=dR (элементарное сопротивление), запишем закон Ома в интегральной форме:
Закон Ома в интегральной форме для неоднородного участка цепи
Проинтегрируем получившееся соотношение на конкретном участке цепи постоянного тока между поперечными сечениями S1 и S2:
интегральный закон Ома для участка цепи
– сопротивление участка,
– работа сторонних сил на перемещении единичного положительного заряда по данному участку цепи ЭДС участка,
– работа электростатических сил на перемещении единичного положительного заряда по данному участку цепи (напряжение участка),
– абсолютная величина работы сил сопротивления на перемещении единичного положительного заряда по данному участку цепи (падение напряжения участка).
Запишем значение напряжения при постоянном токе:
Отсюда запишем закон Ома:
Таким образом закон Ома в интегральной форме – это закон изменения механической энергии единичного положительного заряда на этом участке. В арифметическом виде этот закон можно записать так:
Решение задач
Какой будет плотность тока в металлическом проводнике с удельным сопротивлением ρ постоянного сечения, имеющем длину l, если напряжение, которое приложено к проводу равно U?
Закон Ома для участка цепи утверждает: сила тока I прямо пропорциональна напряжению U на участке цепи и обратно пропорциональна сопротивлению R
.
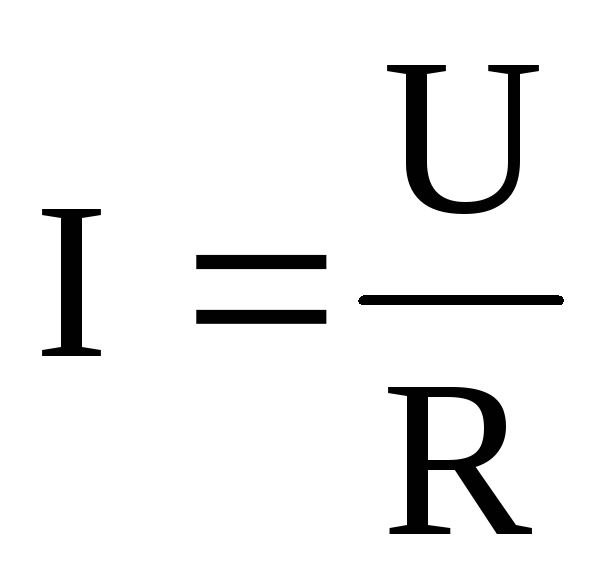Закон Ома можно представить в дифференциальной форме. Через поперечное сечение проводника течет ток силой dI равной dI = jdS. Напря- жение, приложенное на концах проводника, будет равно Е·dl (т.к. 
и dφ = -Edl). Для проводника постоянного сечения длиной l будем иметь
.
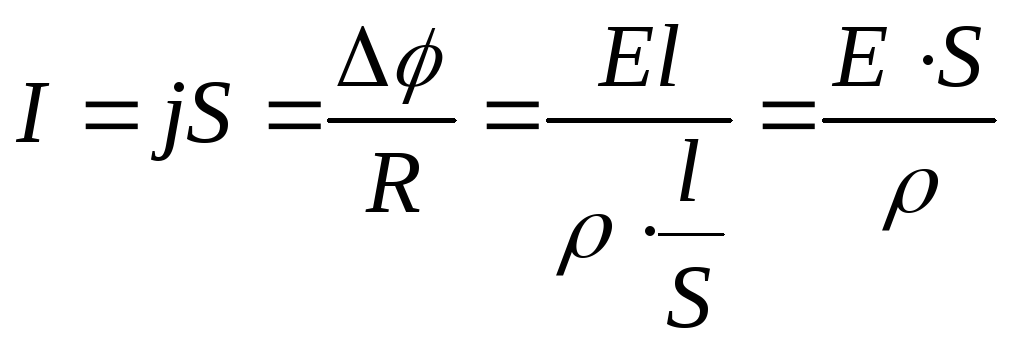Отсюда 
, где
– удельная проводимость проводника. Таким образом, выражениезакона Ома в дифференциальной форме в векторном виде будет
Плотность тока в проводнике прямо пропорциональна напряженности электрического поля в нем.
Рассмотрим замкнутую электрическую цепь, содержащую ЭДС. Источник тока в такой цепи обладает внутренним сопротивлением r. Сопротивление внешней части цепи R называют внешним или сопротивлением нагрузки. Падение напряжения на внутреннем участке цепи равно U1 = Ir, а на внешнем – U =IR. При замкнутой внешней цепи ЭДС источника тока ؏ равна сумме падений напряжения на внутреннем сопротивлении источника тока и во внешней цепи, ؏ = Ir + IR, откуда
Это есть выражение закона Ома в интегральной форме.
Закон Джоуля-Ленца в дифференциальной и интегральной форме
Опытом установлено, что если в проводнике течет ток, то работа сторонних сил расходуется на его нагревание. Предположим, что на концах участка проводника имеется разность потенциалов U = φ1 – φ2.
Тогда работа по переносу заряда q на этом участке равна
Если ток постоянный, то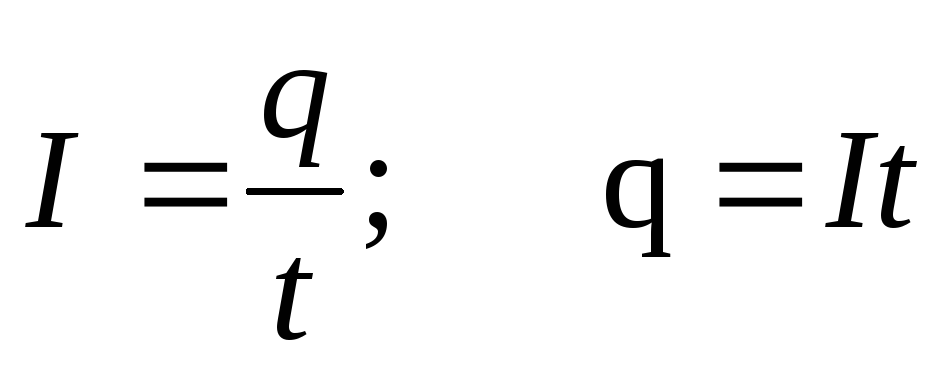 
иA = I U t.
Эта работа равна количеству теплоты Q и формула Q = I U t выражает закон Джоуля-Ленца в интегральной форме.
Используя выражение закона Ома 
получим
.
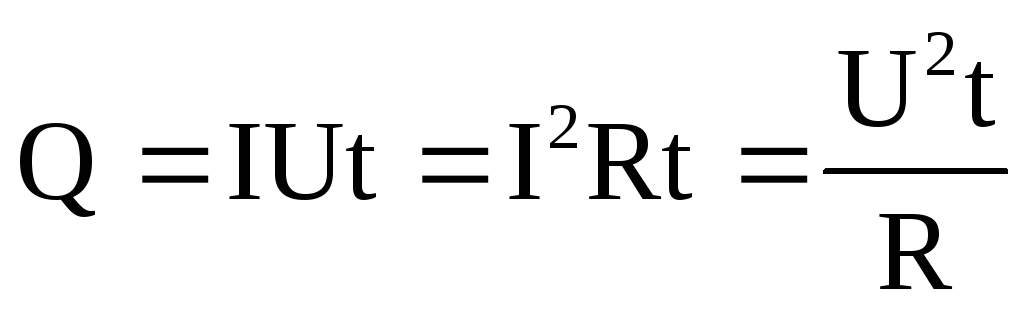Преобразуем закон Джоуля–Ленца. Введем плотность тепловой мощности w – величину, равную энергии, выделяемой за время t прохождения тока в единице объема проводника:
,
где S – сечение, l – длина проводника. Подставляя Q = I 2 R t и 
, получим 
.
Здесь 
– плотность тока,
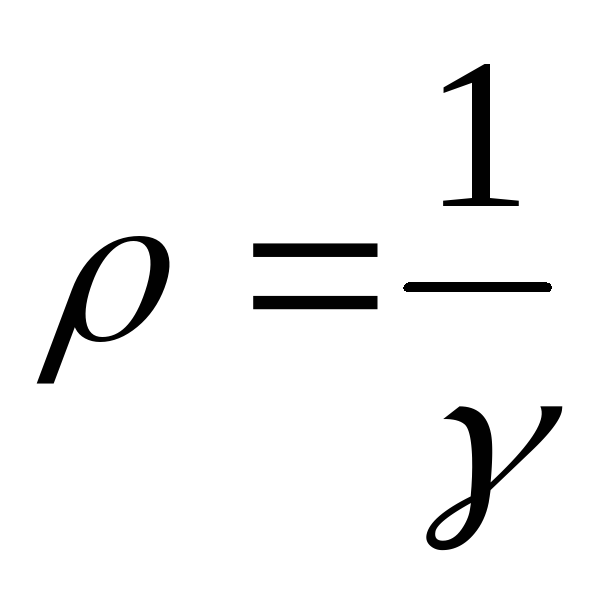, и учитывая, чтоj = γE, получим
.
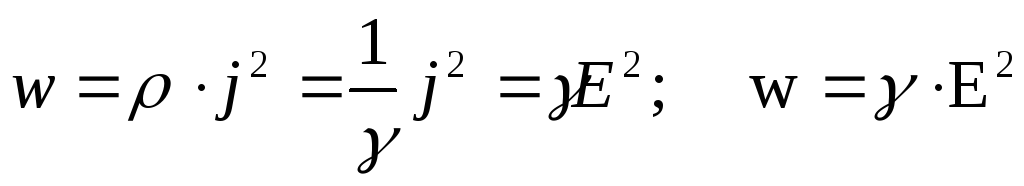Это есть выражение закона Джоуля-Ленца в дифференциальной форме. Плотность тепловой мощности в проводнике, по которому течет ток, прямо пропорциональна квадрату напряженности поля в проводнике. Коэффициентом пропорциональности является удельная проводимость проводника.
Вывод законов Ома и Джоуля-Ленца из классических электронных представлений
Какова природа носителей тока в металлах? В 1901 г. Рикке проделал опыты: через 3 цилиндра, установленных друг на друга в течение 3-х лет пропускал постоянный ток. Был пропущен заряд, равный 3,5·10 6 Кл. Взвешивание показало неизменный вес цилиндров. Исследование торцов цилиндров не показало следов переноса вещества. Из этого был сделан вывод, что носители заряда не ионы, а открытые Томпсоном в 1897 г. электроны.
Чтобы отождествить носители заряда с электронами, нужно было определить знак и величину удельного заряда носителей.
Если в металле имеются легко перемещающиеся заряженные частицы, то при торможении металлического проводника эти частицы должны некоторое время продолжать двигаться по инерции, в результате чего в проводнике возникнет импульс тока и будет перенесен некоторый заряд.
Мандельштам и Папалекси в 1913 г. проделали такой опыт – они приводили в быстрое крутильное колебание катушку с проводом вокруг ее оси. К концам катушки подключили телефон, в котором был слышен звук, обусловленный импульсами тока. Был получен качественный результат – зарегистрирован импульс тока.
Толмен и Стюарт в 1916 г. получили количественный результат. Катушка с проводом длиной 500 м приводилась во вращение со скоростью v=300 м/с. Катушка резко тормозилась и с помощью баллистического гальванометра измеряли заряд, протекавший в цепи во время торможения. Вычисленное значение отношения заряда к массе e/m получалось очень близким для электронов. Таким образом было доказано, что носителем тока являются электроны. Исходя из представлений о свободных электронах была создана классическая теория электропроводности металлов в предположении, что:
– электроны в металле ведут себя подобно молекулам идеального газа;
– движение электронов подчиняется законам классической механики;
– взаимодействие электронов сводится к соударениям с ионами кристалли-ческой решетки;
– силами взаимодействия между электронами можно пренебречь и они между собой не сталкиваются;
– электроны в отсутствие электрического поля движутся хаотически.
Вычислим плотность тока j в проводнике, возникающего под действием поля напряженностью Е.
По определению плотность тока j = n e – это заряд, переносимый через единицу площади S = 1м 2 за единицу времени t=1 с; n – концентрация электронов, е – заряд электрона, – средняя скорость упорядоченного движения электронов.
На каждый электрон действует сила F = eE = ma, поэтому электрон приобретает ускорение 
и к концу свободного пробега он достигнет скорости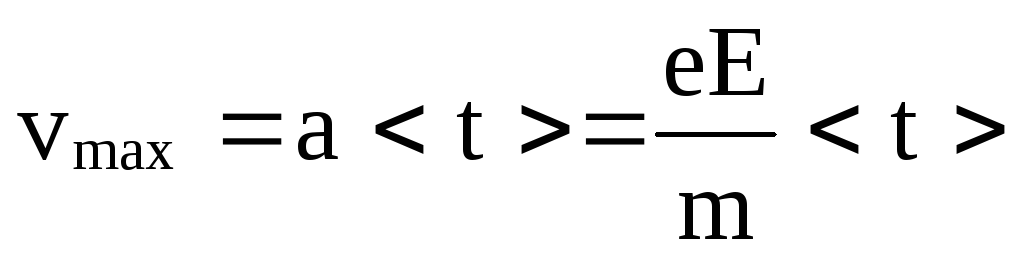
, а средняя скорость =vmax/2.
Если – средняя скорость теплового хаотичного движения электронов, а средняя длина свободного пробега электронов , то среднее время между соударениями = 
. Подставляя в формулу для получим:
.
Подставляя в формулу для j, получим
,
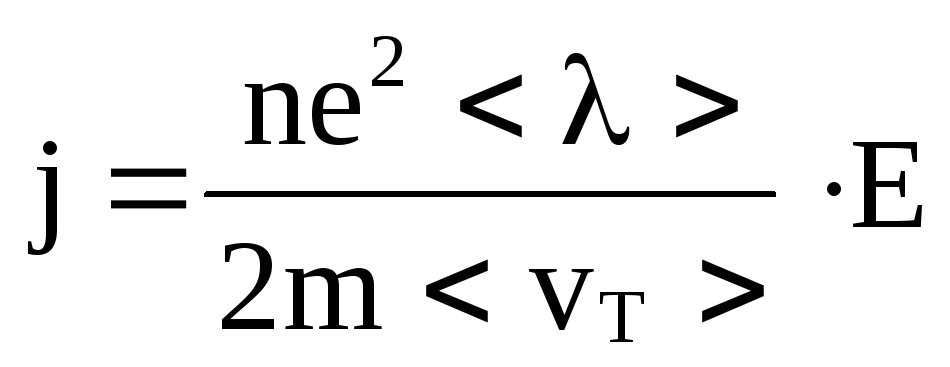т.е. плотность тока прямо пропорциональна Е, а это и есть выражение закона Ома в дифференциальной форме. Если положить, что
то j = γ E.
Удельная проводимость γ
T, поэтому проводимость снижается с ростом температуры, а удельное сопротивление 
повышается с ростом температуры. К концу свободного пробега электрон приобретает кинетическую энергию
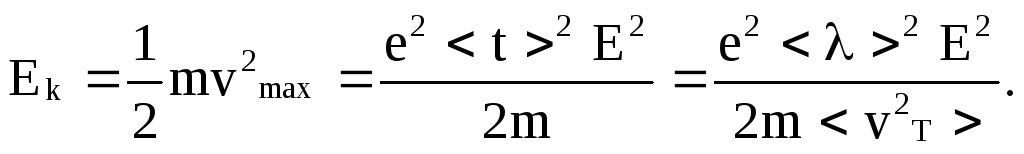
Предполагается, что вся энергия при соударении передается узлу кристаллической решетки и переходит в тепло. За 1 с электрон испытывает / cоударений, а значит выделяет во столько же раз больше тепла. Если в единице объема n электронов, то в единице объема за единицу времени выделится количество тепла
.
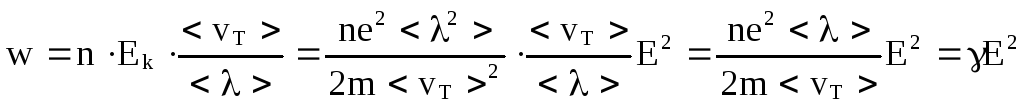Таким образом, 
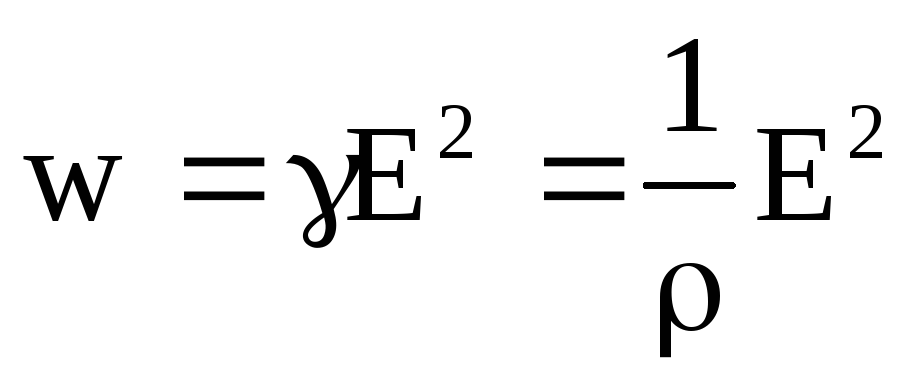– выражение закона Джоуля-Ленца в дифференциальной форме.