Содержание
Знаменитый русский физик Ленц и английский физик Джоуль, проводя опыты по изучению тепловых действий электрического тока, независимо друг от друга вывели закон Джоуля-Ленца. Данный закон отражает взаимосвязь количества теплоты, выделяемого в проводнике, и электрического тока, проходящего по этому проводнику в течение определенного периода времени.
Свойства электрического тока
Когда электрический ток проходит через металлический проводник, его электроны постоянно сталкиваются с различными посторонними частицами. Это могут быть обычные нейтральные молекулы или молекулы, потерявшие электроны. Электрон в процессе движения может отщепить от нейтральной молекулы еще один электрон. В результате, его кинетическая энергия теряется, а вместо молекулы происходит образование положительного иона. В других случаях электрон, наоборот, соединиться с положительным ионом и образовать нейтральную молекулу.

В процессе столкновений электронов и молекул происходит расход энергии, в дальнейшем превращающейся в тепло. Затраты определенного количества энергии связаны со всеми движениями, во время которых приходится преодолевать сопротивление. В это время происходит превращение работы, затраченной на преодоление сопротивления трения, в тепловую энергию.
Сопротивление в электрических проводниках обладает теми же качествами, как и у обычного сопротивления. Для того чтобы провести ток через проводник, источником тока затрачивается определенное количество энергии, превращающейся в тепло. Данное превращение как раз и отражает закон Джоуля – Ленца, известного также, как закон теплового действия тока.
Закон джоуля Ленца формула и определение
Согласно закону джоуля Ленца, электрический ток, проходящий по проводнику, сопровождается количеством теплоты, прямо пропорциональным квадрату тока и сопротивлению, а также времени течения этого тока по проводнику.

В виде формулы закон Джоуля-Ленца выражается следующим образом: Q = I 2 Rt, в которой Q отображает количество выделенной теплоты, I – силу тока, R – сопротивление проводника, t – период времени. Величина "к" представляет собой тепловой эквивалент работы и применяется в тех случаях, когда количество теплоты измеряется в калориях, сила тока – в амперах, сопротивление – в Омах, а время – в секундах. Численное значение величины к составляет 0,24, что соответствует току в 1 ампер, который при сопротивлении проводника в 1 Ом, выделяет в течение 1 секунды количество теплоты, равное 0,24 ккал. Поэтому для расчетов количества выделенной теплоты в калориях применяется формула Q = 0,24I 2 Rt.
При использовании системы единиц СИ измерение количества теплоты производится в джоулях, поэтому величина "к", применительно к закону Джоуля-Ленца, будет равна 1, а формула будет выглядеть: Q = I 2 Rt. В соответствии с законом Ома I = U/R. Если это значение силы тока подставить в основную формулу, она приобретет следующий вид: Q = (U 2 /R)t.
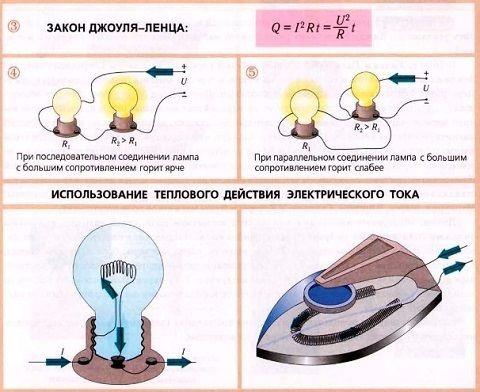
Основная формула Q = I 2 Rt очень удобна для использования при расчетах количества теплоты, которое выделяется в случае последовательного соединения. Сила тока во всех проводниках будет одинаковая. При последовательном соединении сразу нескольких проводников, каждый из них выделит столько теплоты, которое будет пропорционально сопротивлению проводника. Если последовательно соединить три одинаковые проволочки из меди, железа и никелина, то максимальное количество теплоты будет выделено последней. Это связано с наибольшим удельным сопротивлением никелина и более сильным нагревом этой проволочки.
При параллельном соединении этих же проводников, значение электрического тока в каждом из них будет различным, а напряжение на концах – одинаковым. В этом случае для расчетов больше подойдет формула Q = (U 2 /R)t. Количество теплоты, выделяемое проводником, будет обратно пропорционально его проводимости. Таким образом, закон Джоуля – Ленца широко используется для расчетов установок электрического освещения, различных отопительных и нагревательных приборов, а также других устройств, связанных с преобразованием электрической энергии в тепловую.
Закон Джоуля-Ленца. Работа и мощность электрического тока
В случае, когда проводник неподвижен и химических превращений в нем не происходит, то работа тока целиком расходуется на нагревание проводника. Количество теплоты, выделяющееся в проводнике за конечный промежуток времени при прохождении постоянного тока I, рассчитывается по формуле
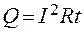 . (2.7)
. (2.7)
Формула (2.7) выражает закон Джоуля-Ленца для участка цепи постоянного тока: количество теплоты, выделяемое постоянным электрическим током на участке цепи, равно произведению квадрата силы тока на время его прохождения и электрическое сопротивление этого участка цепи.
Так как IR = U, то формулу (2.7) можно переписать в виде
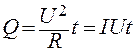 . (2.8)
. (2.8)
Если сила тока изменяется со временем, то количество теплоты, выделяющееся за время t, вычисляется по формуле
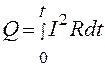 . (2.9)
. (2.9)
Закон Джоуля-Ленца в дифференциальной форме (для данной точки проводника с током) имеет вид
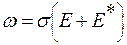 , (2.10)
, (2.10)
где ω − плотность тепловой мощности; σ − удельная электропроводность; Е− напряженность электрического поля в данной точке проводника; Е * − напряженность поля сторонних сил.
Примеры решения задач
Задача 1. За время τ = 20 с при равномерно возраставшей силе тока от нуля до Io в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Найти Io.
| Io – ? | Решение: Так как ток равномерно возрастает, то зависимость силы тока от времени имеет вид 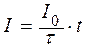 . (1) . (1) |
| τ = 20 с R = 5 Ом Q = 4 кДж |
По закону Джоуля-Ленца за время dt в проводнике выделится количество тепла
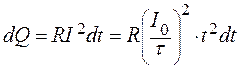 .
.
Полное количество тепла за время от 0 до τ
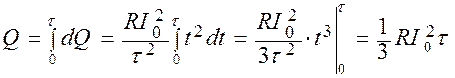 .
.
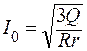 ;
; 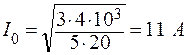 .
.
Задача 2. При включении электромотора в сеть с напряжением U = 220 В он потребляет ток I = 5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление обмотки мотора R = 6 Ом.
| Pп – ? η – ? | Решение: Полная мощность, потребляемая мотором: 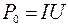 , Р0 = 1100 Вт. , Р0 = 1100 Вт. |
| U = 220 В I = 5 А R = 6 Ом |
Мощность, выделяющаяся в виде тепла:
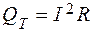 .
.
Полезная мощность (механическая)
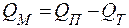 .
.
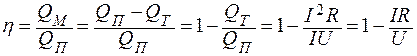 ;
;
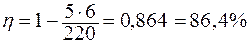 .
.
Задача 3. Источник тока с ЭДС замкнут на реостат. При силе тока I1 = 0,2 А и I2 = 2,4 А на реостате выделяется одинаковая мощность. Найти:
1) при какой силе тока на реостате выделяется максимальная мощность?
2) чему равна сила тока короткого замыкания?
| I – ? Iкз – ? | Решение: При силе тока I1 на реостате выделяется мощность 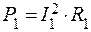 , при силе тока I2 , при силе тока I2 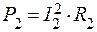 , , |
| I1 = 0,2 А | |
| I2 = 2,4 А P1 = P2 |
где R1 и R2 – сопротивления реостата в каждом случае. По условию P1 = P2, поэтому
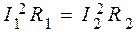 . (1)
. (1)
По закону Ома для полной цепи
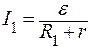 , (2)
, (2)
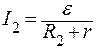 . (3)
. (3)
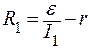 ;
; 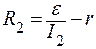 ,
,
подставив их в (1), получаем:
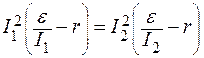 .
.
Отсюда находим отношение 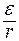 :
:
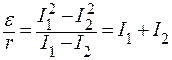 ;
;
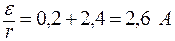 .
.
Максимальная мощность выделяется при условии R = r, при этом ток
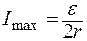 . (4)
. (4)
Ток короткого замыкания
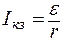 . (5)
. (5)
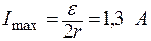 ;
; 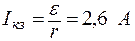 .
.
Задача 4. При изменении внешнего сопротивления с R1 = 6 Ом до R2 = 21 Ом. КПД схемы увеличился вдвое. Чему равно внутреннее сопротивление источника тока r ?
| r − ? | Решение: При сопротивлении R1 КПД источника тока 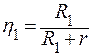 , а при сопротивлении R2 , а при сопротивлении R2 |
| R1 = 6 Ом R2 = 21 Ом η2 = 2η1 |
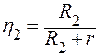 .
.
Так как по условию задачи η2=2η1, то
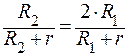 .
.
Отсюда выражаем r:
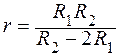 ;
;
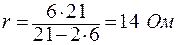 .
.
Ответ: r = 14 Ом.
Задача 5. Две батареи с ЭДС ε1 = 20 В и ε2 = 30 В и внутренними сопротивлениями r1 = 4 Ом и r2 = 60 Ом соединены параллельно и подключены к нагрузке R = 100 Ом. Найти: 1) мощность, которая выделяется в нагрузке; 2) параметры ε и r генератора, которым можно заменить батареи без изменения тока в нагрузке; 3) КПД этого генератора.
| P – ? ε, r – ? η – ? | Решение: 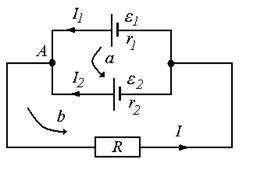 Рис. 52 Рис. 52 |
| ε1 = 20 В ε2 = 30 В r1 = 4 Ом r2 = 60 Ом R = 100 Ом |
Используя правила Кирхгофа, найдем токи I1, I2, I в узле A:
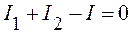 . (1)
. (1)
Для контура a с обходом против часовой стрелки
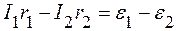 . (2)
. (2)
Для контура b с обходом против часовой стрелки
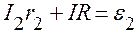 . (3)
. (3)
Решим систему линейных уравнений (1) – (3) относительно I1, I2, I.
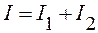 . (4)
. (4)
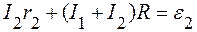
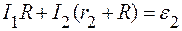 . (5)
. (5)
Умножая уравнение (2) на R, а уравнение (5) – на r1, и складывая их, получаем:
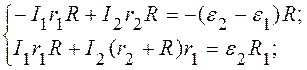
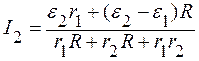 . (6)
. (6)
Подставляя (6) в выражение (2), находим I1:
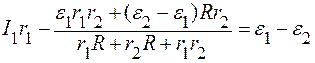 .
.
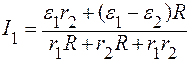 . (7)
. (7)
Подставляя выражения (6) и (7) в (4), находим I:
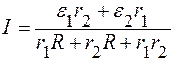 . (8)
. (8)
В нагрузке выделяется мощность:
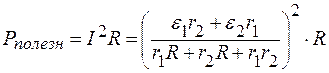 ;
;
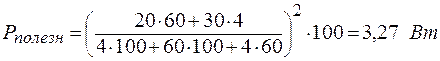 .
.
Находим параметры генератора. Если данные в задаче батареи заменить на одну с ЭДС ε и внутренним сопротивлением r, то через сопротивление R потек бы ток
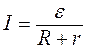 . (9)
. (9)
Преобразуем выражение (8), поделив числитель и знаменатель дроби на (r1+r2), получим
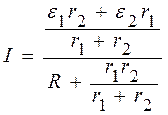 . (10)
. (10)
Для того чтобы эти выражения были одинаковыми, необходимо выполнение условий:
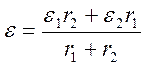 ;
;
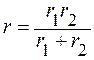 ;
;
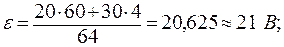
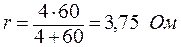 .
.
КПД этого генератора в данной схеме
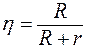 ;
;
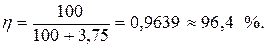
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8852 –  | 7556 –
| 7556 –  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
 При протекании по проводнику электрический ток оказывает на него тепловое действие, во время которого выделяется определенное значение количества теплоты. Для его расчета применяется закон Джоуля-Ленца, который получил широкое применение при проектировании и изготовлении всех устройств, работающих от электричества.
При протекании по проводнику электрический ток оказывает на него тепловое действие, во время которого выделяется определенное значение количества теплоты. Для его расчета применяется закон Джоуля-Ленца, который получил широкое применение при проектировании и изготовлении всех устройств, работающих от электричества.
Общие сведения
В 1941 году английским физиком Джеймсом Джоулем и, независимо от него, в 1942 году русским ученым Эмилием Ленцем было открыто уравнение Джоуля-Ленца. Оно позволяет рассчитать по формуле количество теплоты в электрической цепи, выделяемое при прохождении электротока через проводник. Значение количества теплоты, выделяемое проводником при протекании тока через него, зависит от напряжения, времени, силы тока и сопротивления проводника. Открытие позволило точно рассчитывать схемы различных устройств при их проектировании.

Прежде чем сформулировать закон Джоуля-Ленца, следует рассмотреть и понять физический смысл основных и производных величин, от которых зависит, какое количество теплоты выделяет проводник при прохождении через него электротока.
Разность потенциалов
Научно доказано, что каждое вещество состоит из атомов, которые также состоят из элементарных или субатомных частиц. К ним относятся следующие: электроны, протоны и нейтроны. Атом в исходном состоянии имеет нейтральный заряд, поскольку количество протонов и электронов равны и, следовательно, справедливо равенство положительного и отрицательного зарядов, и они компенсируют друг друга.
 Однако возникают случаи «захвата» атомом электрона другого атома. Если атом захватывает электрон, то он называется отрицательным ионом, а при потере преобразовывается в положительный. В результате потери или притяжения субатомной отрицательно заряженной частицы образуется электромагнитное поле, составляющая которого зависит от заряда иона.
Однако возникают случаи «захвата» атомом электрона другого атома. Если атом захватывает электрон, то он называется отрицательным ионом, а при потере преобразовывается в положительный. В результате потери или притяжения субатомной отрицательно заряженной частицы образуется электромагнитное поле, составляющая которого зависит от заряда иона.
Разность между положительной и отрицательной составляющими является напряжением, единицей измерения которого является вольт (обозначение: В или V). Чем больше разница, тем больше напряжение. В некоторых источниках его еще называют разностью потенциалов, величину которой можно измерять при помощи вольтметра или рассчитать, используя формулы. При соединении потенциалов с противоположными знаками образуется электрический ток, который представляет упорядоченное движение заряженных частиц, под действием силы электромагнитного поля имеет векторное направление.
В научной литературе можно встретить такое определение: электрическим напряжением является работа, которая выполняется при перемещении точечного заряда. Таким образом, 1 В — это напряжение между двумя точечными положительным и отрицательным зарядами, равными 1 Кл, на перемещение которых тратится энергия электромагнитного поля 1 Дж. Вспомогательными единицами измерения являются следующие: 1 кВ = 1000 В, 1 МВ = 10 6 В, 1 мВ = 10^(-3) и т. д.
Сила тока
Сила тока (I) — величина, равная количеству заряженных частиц, которые проходят через проводник за единицу времени. Единица измерения — ампер (А), а с помощью амперметра можно измерять ее значение. Прибор подключается последовательно с потребителем в электрическую цепь. Если через площадь поперечного сечения проводника за 1 секунду проходит количество заряда, равное 1 Кл, то эта величина является силой тока в 1 А.
Математическая запись нахождения силы тока имеет вид: I = Qz / t, где Qz — значение заряда, а t — единица времени. Кроме того, существуют и дополнительные единицы измерения: 1 mА = 10^(-3) A, 1 кА = 1000 А и т. д. Электрический ток бывает следующих видов:
 Переменный ток подчиняется определенному закону, который характеризует изменение амплитуды и направления протекания. Основной характеристикой является частота, согласно которой происходит разделение на синусоидальный и несинусоидальный токи. Графиком синусоидального типа тока является синусоида, формула которой зависит от максимальной амплитуды Imax и угловой частоты w. Она имеет следующий вид: i = Imax * sin (w * t).
Переменный ток подчиняется определенному закону, который характеризует изменение амплитуды и направления протекания. Основной характеристикой является частота, согласно которой происходит разделение на синусоидальный и несинусоидальный токи. Графиком синусоидального типа тока является синусоида, формула которой зависит от максимальной амплитуды Imax и угловой частоты w. Она имеет следующий вид: i = Imax * sin (w * t).
Для расчета значения угловой частоты необходимо значение частоты тока в сети (f), которое подставляется в формулу: w = 6,2832 * f. Постоянный ток не изменяет направление своего движения по проводнику, однако его значение может меняться.
Электрическое сопротивление
Вещества по проводимости электричества можно классифицировать на проводники, полупроводники и диэлектрики. К первому типу относятся все вещества, которые хорошо проводят ток. Эта особенность обуславливается наличием свободных носителей заряда, информацию о которых можно получить из электронной конфигурации элементов периодической системы Д. И. Менделеева.
 К проводникам относят следующие вещества: металлы, электролиты и ионизированный газ. В металлах электроны являются носителями заряда. В жидкостях (электролитах) носителями заряда являются анионы и катионы: первые обладают положительным зарядом, а вторые — отрицательным. При электролизе анионы притягиваются электродом, который является отрицательно заряженным (катодом), а на катионы действует положительный заряд анода. Функцию носителей заряда в газах выполняют отрицательно заряженные электроны и ионы.
К проводникам относят следующие вещества: металлы, электролиты и ионизированный газ. В металлах электроны являются носителями заряда. В жидкостях (электролитах) носителями заряда являются анионы и катионы: первые обладают положительным зарядом, а вторые — отрицательным. При электролизе анионы притягиваются электродом, который является отрицательно заряженным (катодом), а на катионы действует положительный заряд анода. Функцию носителей заряда в газах выполняют отрицательно заряженные электроны и ионы.
При повышении температуры проводника происходит взаимодействие атомов между собой, в результате которого разрушается кристаллическая решетка и появляются свободные носители заряда. При протекании тока происходит взаимодействие с узлами решетки и с электронами проводника, при котором движение упорядоченных заряженных частиц замедляется и выделяется тепловая энергия, а затем снова скорость их движения возвращается в исходное состояние, благодаря воздействию электромагнитного поля. Это физическое свойство называется электрическим сопротивлением проводника, при нагревании которого его величина возрастает.
Полупроводники — вещества, проводящие ток только при определенных условиях. Функцию носителей заряда выполняют электроны и дырки. При каком-либо воздействии внешней энергии (например, тепловой) происходит уменьшение силы притяжения между ядром и электронами, при котором некоторые из них «вырываются» и становятся свободным, а на их месте образуются дырки.
Происходит образование электромагнитного поля положительной составляющей и к ней притягивается соседняя субатомная частица с отрицательным зарядом. Этот процесс повторяется и приводит к движению дырок. Сопротивление вещества (проводника или полупроводника) зависит от следующих факторов:
- Температурных показателей.
- Типа вещества.
- Длины.
- Площади сечения.
- Значения силы тока и напряжения.
- Вида тока.

Диэлектрики — группа веществ, которые не могут проводить ток, поскольку в них отсутствуют какие-либо носители электрического заряда. Сопротивление или электропроводимость обозначается буквой R и является взаимодействием заряженных частиц, движущихся упорядочено, с узлами кристаллической решетки. Единицей его измерения является Ом.
Характеристика мощности
Мощностью электротока (P) называют количество работы, которое им совершается за единицу времени. Для постоянного и переменного токов мощность вычисляется по разным соотношениям. В цепи постоянного тока значения его силы (I) и напряжения (U) равны мгновенным значениям. Формула мощности записывается в следующем виде: P = U * I. Для цепи, в которой соблюдается закон Ома, формула принимает следующий вид: P = sqr (I) * R = sqr (U) / R.
 Для полной цепи формула включает значение электродвижущей силы (e): P = I * e. Если нужно учитывать значение внутреннего сопротивления источника питания (Rвн), то формулу нужно править при условии поглощения (использование в цепи электродвигателя или при зарядке аккумулятора) следующим образом: P = I * e — sqr (I) * Rвн = I * (e — (I * Rвн)).
Для полной цепи формула включает значение электродвижущей силы (e): P = I * e. Если нужно учитывать значение внутреннего сопротивления источника питания (Rвн), то формулу нужно править при условии поглощения (использование в цепи электродвигателя или при зарядке аккумулятора) следующим образом: P = I * e — sqr (I) * Rвн = I * (e — (I * Rвн)).
При наличии в цепи генератора или гальванического элемента (условие отдачи электроэнергии), формула принимает следующий вид: P = I * (e + (I * Rвн)). Однако эту формулу нельзя применять для расчета мощности переменного тока, поскольку он изменяется с течением времени. В цепях переменного тока существует понятие активной, реактивной и полной мощностей:
- Активная определяется с учетом среднеквадратичных значений U и I, а также углом сдвига фаз (a): Pа = I * U * cos (a).
- Реактивная (Qр): Qp = U * I * sin (a).
- Полная (S): S = sqrt (sqr (Pа) + sqr (Qp)).
Значение Qp>0 при наличии в цепи индуктивной нагрузки, а при емкостной — Qp Запись закона Джоуля-Ленца
Формулировка уравнения Джоуля-Ленца следующая: количество теплоты Q, которое выделилось за единицу времени t на участке цепи, прямо пропорционально произведению сопротивления R на квадрат силы тока I, протекающей через этот участок. Формула закона Джоуля-Ленца имеет вид: Q = a * sqr (I) * R * t. Литера «а» является температурным коэффициентом, который равен 1 при условии, что количество теплоты получается в джоулях. Если принять его равным 0,24, то результат будет измеряться в калориях. Поскольку а = 1, то формула Ленца будет выражаться кратко в таком виде: Q = sqr (I) * R * t.
При перегреве проводника может возникнуть короткое замыкание, которое приводит к выходу аппаратуры из строя. Оно может также быть причиной пожара. Для избежания таких ситуаций в электротехнике применяются плавкие предохранители, которые позволяют прекратить подачу электричества на устройство.

Закон позволяет найти необходимые параметры электрического тока, чтобы избежать перегрева и пожара. Основные соотношения для расчета составляющих величин закона в цепях постоянного тока следующие:
- Закон Ома для участка и полной цепи: I = U / R и i = e / (R + Rвн).
- Q = U * I * t.
- Q = e * i * t.
- Q = (t * sqr (U)) / R.
- Q = (t * sqr (e)) / (R + Rвн).
- Q = P * t.
Различие математической записи закона в цепях с переменным и постоянным токами обусловлено их свойствами и параметрами, а также появлением нагрузок активной и реактивной составляющей. Кроме того, ток переменной составляющей постоянно изменяется во времени. Основные соотношения:
- Закон Ома: i = U / Z, где Z — полное сопротивление цепи. Оно включает в себя активную, индуктивную и емкостную нагрузки.
- Q = S * t = t * [sqrt (sqr (Pа) + sqr (Qp))].
- Q = U * i * t, где U и i — действующие значения напряжения и тока, которые измеряются при помощи вольтметра и амперметра соответственно. Формулу в таком виде можно применять для примерного расчета Q, причем в цепях, состоящих только из активной нагрузки.
- Запись закона с учетом в электрической цепи активной и реактивной нагрузок: Q = sqr (i) * Z * t.

Примеров применения уравнения Джоуля-Ленца достаточно много, одним из которых является обыкновенная лампа накаливания с вольфрамовой нитью. Свечение происходит из-за высокого напряжения и материала, из которого изготовлена нить накаливания. Электродуговая сварка работает тоже по этому закону, поскольку ток проходит через электрод и оказывает на него тепловое действие, при котором образуется сварочная дуга. Благодаря закону, можно правильно рассчитать и сделать вывод о применении радиокомпонента в какой-либо схеме.
Таким образом, уравнение Джоуля-Ленца играет важную роль в электротехнике, поскольку позволяет произвести точные расчеты радиокомпонентов схемы, исключая перегрев деталей и пожар.
