Особенностью преобразователей этого вида заключается в том, что напряжение на его выходе непосредственно соответствует пиковому (амплитудному) значению напряжения, поданного на вход преобразователя. Преобразователь должен содержать элемент, запоминающий пиковое значение напряжения. Обычно это конденсатор, заряжаемый через диод до пикового значения.
Необходимо отметить, что амплитудные преобразователи – самые широкополосные преобразователи напряжения переменного тока в напряжение постоянного тока. Далее приведены схемы часто встречающихся преобразователей: с открытым и закрытым входом.
Для всех преобразователей должны выполняться условия:
– постоянная времени цепи заряда конденсатора τз=RiC ( здесь Ri– внутренне сопротивление диода) должна быть много меньше постоянной времени τр=RC цепи разряда конденсатора;
– значение τз £ 1/fв= Тв (период самого высокочастотного измеряемого напряжения);
– значение τр >>1/fн= Тн (период самого низкочастотного напряжения).
а) преобразователь пикового (амплитудного) значения с открытым входом
Рассмотрим работу преобразователя когда к нему приложено синусоидальное напряжение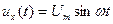 
. В начальный момент времени 
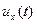полностью приложено к диоду поскольку 
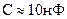>> Сд диода.
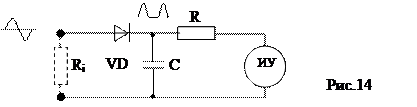Ri
При первой положительной полуволне в цепи диода возникает большой импульс тока, который подзаряжает конденсатор. При каждой положительной полуволне синусоидального напряжения u(t) конденсатор подзаряжается через внутреннее сопротивление диода Ri.
Учитывая, что постоянная времени заряда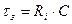 
Рассмотрим работу преобразователя при подаче гармонического сигнала u(t)=Umsinwt.
За несколько положительных полупериодов конденсатор С заряжается через диод почти до значения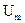 
.Разряжается конденсатор через резистор достаточно большого номинала 
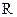, как и в преобразователе с открытым входом.
Основное различие состоит в том, что выходным является напряжение UR, представляющее собой алгебраическую сумму напряжений на конденсаторе С и входного напряжения. После подавления переменной составляющей этого сигнала с помощью фильтра ФНЧ на индикаторном устройстве ИУ будет отображаться постоянная составляющая U0.
 |
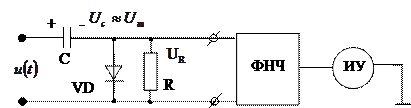Наличие сглаживающего фильтра отличает данную схему от амплитудного преобразователя с открытым входом, где он не нужен.
Если на вход подается напряжение с постоянной составляющей U0, то в зависимости от полярности включения диода преобразователь будет реагировать либо на положительное Um+, либо на отрицательное Um– значение переменной составляющей относительно линии среднего значения U0.
При измерении напряжения без постоянной составляющей А- преобразователи с открытым и закрытым входом дают одно и тоже значение.
Многие пиковые вольтметры хотя и измеряют пиковое значение, но градуируются в среднеквадратических значениях для гармонических сигналов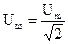 
. Поэтому для измерения среднеквадратического значения сигнала произвольной формы необходимо воспользоваться формулой: 
.
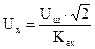Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10606 – 
| 7337 – 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Уровень переменного напряжения можно определить по амплитудному, среднеквадратическому, среднему или средневыпрямленному значениям. Амплитуда(пиковое значение) Um-наибольшее мгновенное значение напряжения за интервал наблюдения или за период. Измеряемые на практике напряжения могут иметь различный вид, например, форму импульсов, синусоидального или несинусоидального колебаний- суммы синусоиды с постоянной составляющей и т.д. При разнополярных несимметричных кривых формы напряжения различают два амплитудных значения: положительное Um 
и отрицательное Um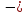
.
Среднее квадратическое значение напряжения есть корень квадратный из среднего квадрата его мгновенного значения за время измерения(за период):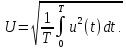 
Если периодический сигнал несинусоидален, то квадрат среднего квадратического значения равен сумме квадратов постоянной составляющей и средних квадратических значений гармоник :
= 
+
+
+ …
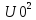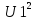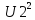Среднее значение(постоянная составляющая) напряжения равно среднему арифметическому всех мгновенных значений за период :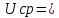 
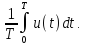
Средневыпрямленное напряжение определяется как среднее арифметическое абсолютных мгновенных значений за период :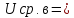 
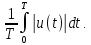
Для напряжения одной полярности среднее и средневыпрямленное значения равны. Для разнополярных напряжений эти значения могут существенно отличаться. Так, для гармонического напряжения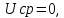 
.
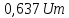Чаще измеряют среднее квадратическое изменение напряжения, так как этот параметр связан с мощностью, нагревом, потерями. Однако проще измерить амплитудное или средневыпрямленное значение и произвести пересчёт с применением коэф. Амплитуды Ка и формы Кф : Ка =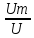 
, Ка =
.
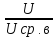В частности, для синусоидальной (гармонической) формы переменного напряжения : Ка = 1,41; Кф = 1,11.
Значения этих коэффициентов для наиболее употребляемых видов сигналов и соотношения между ними даны в табл., где все напряжения для упрощения обозначены буквой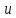 
.
2 Преобразователи пикового значения: с открытым и закрытым входами: схемы, принцип действия.
Преобразователи пикового значения. Особенность преобразователя этого вида заключается в том, что напряжение на его выходе непосредственно соответствует пиковому (амплитудному) значению напряжения, поданного на вход преобразователя. Он должен содержать элемент, запоминающий пиковое значение напряжения. Обычно это конденсатор, заряжаемый через диод до пикового значения.
Необходимо подчеркнуть, что преобразователи пикового значения, которые в дальнейшем для кратности будем называть пиковыми, — самые широкополосные преобразователи напряжения переменного тока в напряжение постоянного тока.
Пиковый (амплитудный) детектор — это детектор, напряжение на выходе которого непосредственно соответствует измеряемому пиковому (амплитудному) значению напряжения. Пиковый детектор должен содержать элемент, запоминающий пиковое значение напряжения. Таким элементом обычно служит конденсатор, заряжаемый через диод до пикового значения.
Пиковые детекторы
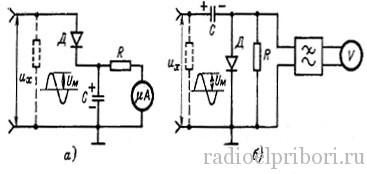
а — с открытым входом;
б — с закрытым входом.
При измерении напряжений, не содержащих постоянной составляющей, детекторы с открытым и закрытым входом дают одинаковые результаты: напряжения на конденсаторах С в обоих случаях весьма близки к Uм и показания обоих вольтметров пропорциональны амплитуде измеряемого напряжения.
Если ко входу (рис. а), подводится напряжение uх = Uо + U ′ мsinωt, в котором содержатся и постоянная и переменная составляющие, то прибор будет измерять пиковое значение Uм =Uо + U ′ м. В случае подачи пульсирующего напряжения на вход детектора с закрытым входом вольтметр измеряет пиковое значение U ′ м напряжения без постоянной составляющей.
Переменный ток (AC – Alternating Current) – электрический ток, меняющий свою величину и направление с течением времени.
Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.
DC – Direct Current – постоянный ток, не меняющий своей величины и направления.
В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.
При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.
Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.
Величина тока будет равна квадратному корню из суммы квадратов двух величин – значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.
Термины AC и DC применимы как для тока, так и для напряжения.
Параметры переменного тока и напряжения
Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:
Период T – время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
Частота f – величина, обратная периоду, равная количеству периодов за одну секунду.
Один период в секунду это один герц (1 Hz)
Циклическая частота ω – угловая частота, равная количеству периодов за 2π секунд.
Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
Начальная фаза ψ – величина угла от нуля (ωt = 0) до начала периода. Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Мгновенное значение – величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:
i = I ampsin(ωt); u = U ampsin(ωt)
С учётом начальной фазы:
i = I ampsin(ωt + ψ); u = U ampsin(ωt + ψ)
Здесь I amp и U amp – амплитудные значения тока и напряжения.
Амплитудное значение – максимальное по модулю мгновенное значение за период.
Может быть положительным и отрицательным в зависимости от положения относительно нуля.
Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) – максимальное отклонение от нулевого значения.
Среднее значение (avg) – определяется как среднеарифметическое всех мгновенных значений за период T.
Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.
Средневыпрямленное значение – среднеарифметическое модулей всех мгновенных значений за период.
Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.
Среднеквадратичное значение (rms) – определяется как квадратный корень из среднеарифметического квадратов всех мгновенных значений за период.
Для синусоидального тока и напряжения амплитудой I amp (U amp) среднеквадратичное значение определится из расчёта:
Среднеквадратичное – это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов. Является объективным количественным показателем для любой формы тока.
В активной нагрузке переменный ток совершает такую же работу за время периода, что и равный по величине его среднеквадратичному значению постоянный ток.
Коэффициент амплитуды и коэффициент формы
Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой амплитудное, среднеквадратичное и средневыпрямленное значения.
Коэффициент амплитуды – отношение амплитудного значения к среднеквадратичному. 
Для синусоидального тока и напряжения коэффициент амплитуды KA = √2 ≈ 1.414
Для тока и напряжения треугольной или пилообразной формы коэффициент амплитуды KA = √3 ≈ 1.732
Для переменного тока и напряжения прямоугольной формы коэффициент амплитуды KA = 1
Коэффициент формы – отношение среднеквадратичного значения к средневыпрямленному. 
Для переменного синусоидального тока или напряжения коэффициент формы KФ 
≈ 1.111
Для тока и напряжения треугольной или пилообразной формы KФ 
≈ 1.155
Для переменного тока и напряжения прямоугольной формы KФ = 1
Замечания и предложения принимаются и приветствуются!