Содержание
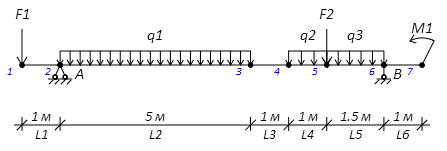
Определение опорных реакций
Построение эпюр поперечных сил и моментов
Просмотр хода решения
Описание
Расчет выполняется по следующей методике:
1. Заменяем распределенную нагрузку ее равнодействующей, которая является сосредоточенной силой. Для равномерно распределенной нагрузки равнодействующая равна произведению интенсивности нагрузки q на длину участка L, на котором она действует: Fq = q*L.
2. Обозначаем опоры. Общепринято их обозначать буквами А и В. Простая балка имеет одну шарнирно-неподвижную и одну шарнирно-подвижную опоры.
3. Освобождаемся от опор и заменяем их действие на балку реакциями.
Реакции опор при такой нагрузке будут только вертикальными.
4. Составляем уравнения равновесия вида: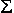 
MA = 0; 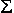MB = 0,
Моментом силы относительно точки называется произведение этой силы на плечо — кратчайшее расстояние от этой точки приложения силы (в общем случае — до линии действия силы).
5. Выполним проверку решения. Для этого составим уравнение равновесия: 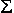Y = 0,
Если оно удовлетворено, то реакции найдены правильно, а если нет, но в решении допущена ошибка.
6. Строим эпюру поперечных сил Qx. Для этого определяем значения поперечных сил в характерных точках. Напомним, что поперечная сила в сечении равна сумме проекций всех сил, расположенных только слева или только справа от рассматриваемого сечения, на ось, перпендикулярную оси элемента. Силу, расположенную слева от рассматриваемого сечения и направленную вверх, считают положительной (со знаком «плюс»), а направленную вниз — отрицательной (со знаком «минус»). Для правой части балки — наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть левее рассматриваемой точки и чуть правее ее. Поперечные силы в этих сечениях обозначаются соответственно Qлев и Qправ.
Найденные значения поперечных сил в характерных точках откладываются в некотором масштабе от нулевой линии. Эти значения соединяются прямыми линиями по следующим правилам:
а) если к участку балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяются прямой линией, параллельной нулевой линии;
б) если на участке балки приложена распределенная нагрузка, то под этим участком значения поперечных сил соединяются прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию.
Соединив все значения поперечных сил по указанным правилам, получим график изменения поперечных сил по длине балки. Такой график называется эпюрой Qx.
7. Строим эпюру изгибающих моментов Мx. Для этого определяем изгибающие моменты в характерных сечениях. Напомним, что изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил (распределенных, сосредоточенных, в том числе и опорных реакций, а также внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то оно считается положительным (со знаком «плюс»), если против — отрицательным (со знаком «минус»), а для правой части наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента: чуть левее рассматриваемой точки и чуть правее ее. Изгибающие моменты в этих точках обозначаются соответственно Млев и Мправ. В точках приложения сил определяется одно значение изгибающего момента.
Полученные значения откладываются в некотором масштабе от нулевой линии. Эти значения соединяются в соответствии со следующими правилами:
а) если на участке балки нет распределенной нагрузки, то под этим участком балки два соседних значения изгибающих моментов соединяются прямой линией;
б) если к участку балки приложена распределенная нагрузка, то под этим участком значения изгибающих моментов для двух соседних точек соединяются по параболе.
В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала определить опорные реакции из уравнений статики, так как и в левую, и в правую отсеченные части для любого сечения, расположенного между опорами, попадает соответствующая реакция.
Для плоской системы число уравнений статики в общем случае равно трем. Если балка загружена только вертикальными нагрузками, то горизонтальная реакция шарнирно-неподвижной опоры равна нулю, и одно из уравнений равновесия (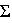 
Fix = 0) обращается в тождество. Таким образом, для определения реакций в опорах шарнирной балки используются два уравнения статики:
1. 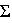МА = 0,
2. 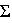МВ = 0.
Условие 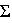Fiy = 0 используется для проверки вычисленных значений опорных реакций.
Пример 5.Построить эпюры Qy и Mx для балки с шарнирным опиранием (рис.8).
1. Вычисляем реакции опор.
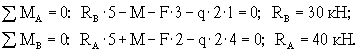
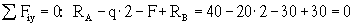
2. Намечаем характерные сечения.
В отличие от консольных балок здесь известны обе опорные реакции, поэтому для любого сечения можно рассматривать как левую, так и правую отсеченную часть.
3. Определяем поперечные силы в характерных сечениях.
Строим эпюру Qy.
4. Определяем изгибающие моменты в характерных сечениях.
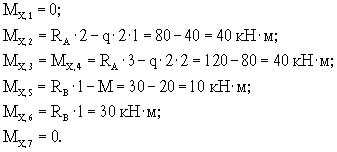
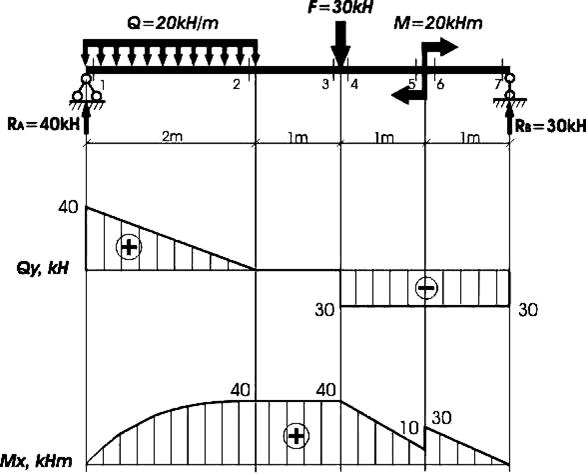
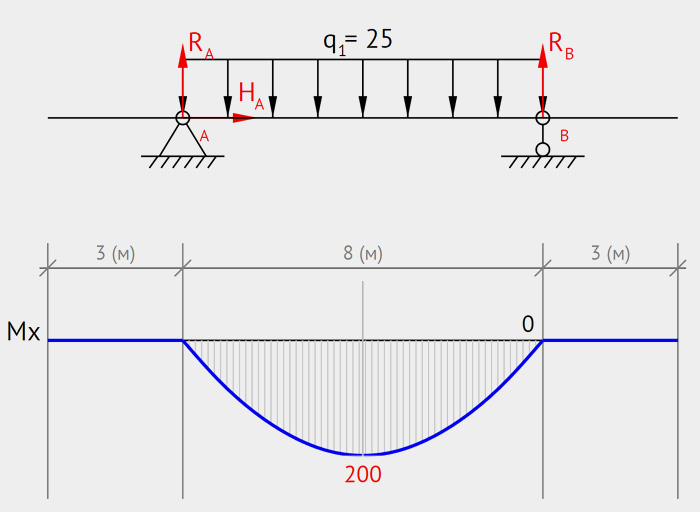
Рис. 8
Строим эпюру Mx
Пример 6. Построить эпюры Qy и Mx для балки на двух опорах с консолью (рис.9,а)
1. Вычисляем опорные реакции.
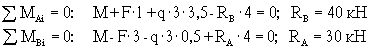
Во втором уравнении равновесия (впрочем, как и в первом) момент от распределенной нагрузки q вычислен без разбиения ее на две части – слева и справа от опоры В, то есть определена равнодействующая нагрузки q – q 
3, ее положение (в середине участка с распределенной нагрузкой), что позволяет определить плечо равнодействующей относительно опоры В и направление создаваемого ею момента. В то же время можно было в уравнении равновесия учитывать отдельно части нагрузки q, приложенные слева и справа от опоры В; при этом второе уравнение равновесия имеет вид:
Вычисленное из этого уравнения значение реакции RA, разумеется, совпадает с полученным ранее.
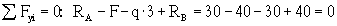
2. Намечаем характерные сечения.
3. Вычисляем поперечную силу и изгибающий момент в характерных сечениях.
Из рассмотрения левой отсеченной части:
Для сечений 5-7 удобнее рассматривать правую отсеченную часть:
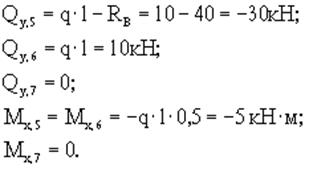
По вычисленным значениям строим эпюры Qy и Mx (рис.9,б,в).
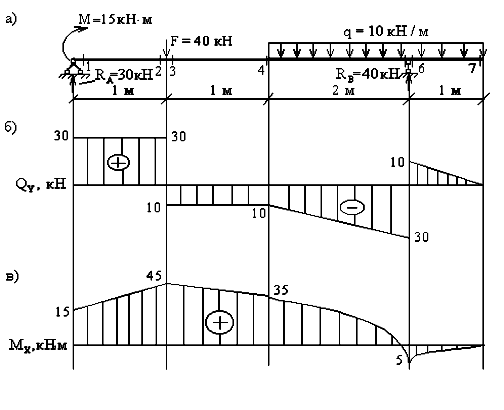
Рис.9
1.11. Правила контроля эпюр Qу И Mx.
Дифференциальные зависимости между Qy определяют ряд закономерностей, которым подчиняются эпюры Qy и Mx.
1. Эпюра Qy является прямолинейной на всех участках; эпюра Mx – криволинейная (квадратная парабола) на участке под равномерно распределенной нагрузкой, причем, выпуклость кривой всегда обращена навстречу нагрузке q, и прямолинейная на всех остальных участках.
2. Под точкой приложения сосредоточенной силы (реакции) на эпюре Qy обязательно должен быть скачок на величину этой силы (реакции). Аналогично, под точкой приложения сосредоточенного момента на эпюре Mx обязателен скачок на величину момента.
3. Если на участке под распределенной нагрузкой эпюра Qy пересекает ось (Qy = 0), то эпюра Mx в этом сечении имеет экстремум.
4. На участках с поперечной силой одного знака эпюра Mx имеет одинаковую монотонность. Так, при Qy > 0 эпюра Mx возрастает слева направо; при Qy
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9396 – 
| 7310 – 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
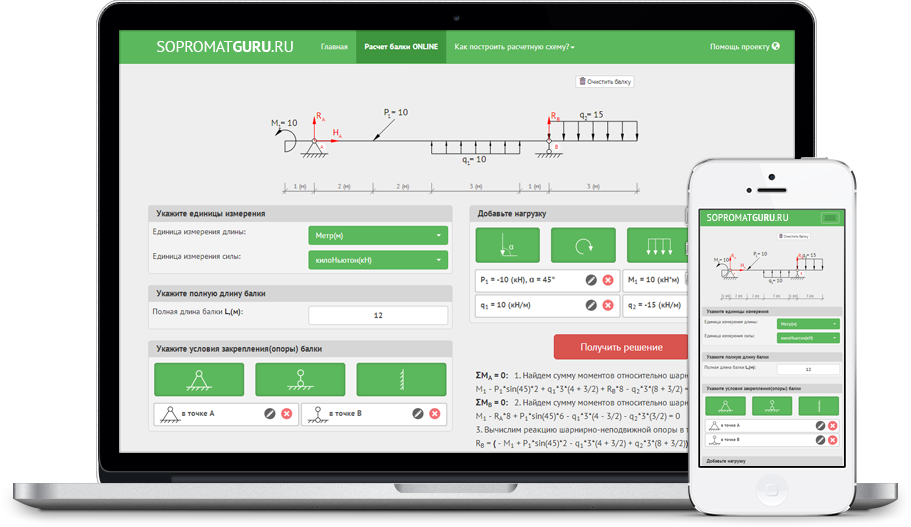
1 – МОБИЛЬНАЯ ВЕРСИЯ САЙТА
Удобная навигация на сайте с мобильных устройств и планшетов
2 – ПОСТРОЕНИЕ ЭПЮР АБСОЛЮТНО БЕСПЛАТНО
Стройте эпюры моментов, поперечных и продольных сил абсолютно бесплатно
3 – ПОДРОБНЫЙ ТЕКСТ РАСЧЕТА
Подробный расчет определения опорных реакций и алгоритм построения эпюр
Данный проект создан с целью помощи в изучении дисциплины сопротивление материалов(сопромат) и теоретической механики. На сегодняшний день проект позволяет выполнить:
- расчет статически-определимой балки с подробным нахождением уравнений реакций опор;
- построение эпюр моментов;
- построение эпюр поперечных сил;
- построение эпюр продальных сил;
- подбор сечения(прямоугольное/квадратное, коробчатое, круглое сплошное, кольцевое, ромбовидное, треугольное, швеллерное, тавровое);
Вскоре мы добавим:
- расчет статически неопределимых балок;
- расчет рам методом сил и методом перемещений;
- расчет ферм методом вырезания узлов.
КАК ЭТО РАБОТАЕТ
Задайте расчетную схему
Укажите длину балки, условия закрепления и нагрузки
Постройте эпюры бесплатно
Выберите необходимые для построения эпюры и параметры расчета
Получите подробный расчет
Выберите тариф и оплатите код доступа для получения подробного текста расчета
ОТЗЫВЫ
Нам доверяют более 167 450 пользователей!
Очень удобная система.
Отлично работает! Нужно обязательно немного разбираться!
Спасибо! Долго не мог разобраться как перешел на ваш сайт и все сразу понятно откуда и как))
Отличная идея. Используется в помощь студентов. Для самопроверки и осознания материала. Спасибо.
Спасибо большое! Все верно получилось
Очень полезная программа. Большое спасибо.
Большое вам человеческое, СПАСИБО.
Удобно и доступно в понимании. Спасибо.
Задачи все оказались правильными)
Замечательнейший ресурс для студентов! Всё понятно, доступно, а главное – быстро. И по сравнению с людьми, которые предлагают делать расчётно-графические работы – гораздо дешевле! Мне понравилось, пойду друзьям расскажу!
Все ок, расчет верный.
Нравится то, что такое имеется в сетях, так как это точно поможет в обучении особенной если есть постоянное желание.
Спасибо вам. Очень помогает!
Большое спасибо! Сдал экзамен на 5! Сервис – на отлично=) из 5 решений осталось 4, а сопромат закончился.
Классный сайт, решение подробное, всё понятно!
Очень интересный сайт, большая практическая помощь.
Спасибо большое, выручили очень!
Чудесный сервис! Очень выручает в сложных ситуациях по сопромату, полезен для проверки своих решений!)
Очень выручило. Интересная задумка!
Спасибо большое!! Все четко и понятно!
Отличный сайт. удобно, понятно и быстро.
Классная штука, помогла!
Вы лучшие. Все успела сделать и разобралась, так как все доступно и понятно расписано. Спасибо вам огромное!
Спасибо большое очень помогло.
Все четко и понятно, спасибо)))
Спасибо очень помогли!
Спасибо, хороший сайт – помог.
Большое спасибо разработчикам, очень помогло)))))
Просто замечательнейший сервис)
Супер! Большое спасибо!
Сайт хороший, помогает студентам, цена адекватная, но побольше бы на сумму давали решений)
Удобно и быстро.
Лучшая программа, которую только можно найти. Благодаря ей быстро научился выполнять расчет балок!
Спасибо, очень помог ваш сайт в расчете!
Благодарствую. Просто, понятно, подробно.
Получил Отлично на экзамене!
Открыл недавно данный сайт для себя. Великолепный сервис для решения задачек. Огромное спасибо разработчикам!
Хороший сайт, помог проверить эпюры, долго не могла понять в чем ошибка.
Отличный сервис! Большое спасибо! Теормех – 4!))
Замечательная программа, спасибо вам!)
У меня все получилось. Всем желаю удачи.
Большое спасибо. Вы спасли.
Очень крутая возможность. Разработчикам просто огромное спасибо!
Всё супер! Спасибо разработчикам!
Отличный сайт, большое спасибо разработчикам, вся наша группа сверялась с данным сайтом, очень помог на контрольных работах!
Спасибо создателям, очень помог!
Огромное спасибо разработчикам!
Очень сильно помогли, спасибо!
Замечательный сайт, очень меня выручил!
Сайт крут, решает на изи, и все как нужно.
Очень понятно, спасибо большое создателям)
Просто нереально крутая вещь ваша программа. Спасибо!)
Спасибо большое за данную программу. Очень помогает в учебе. Санкт-Петербург.
Спасибо очень круто : )
Спасибо)) очень удобно!
Спасибо большое, очень полезный сервис для того, чтобы научиться самому делать расчёты.
Офигенный сайт для заочников на экзамене!
Сайт замечательный и очень помогает, очень благодарен ребятам за создание такого чуда!
Спасибо, очень круто!
Супер удобно и подробно выдал ответ! Экономия времени и нервов. А главное возможность сравнить со своим расчётом и найти ошибку. Огромное вам спасибо .
Круто, спасибо, очень помогли, продолжайте в том же духе ребята!!
Спасибо большое! Очень хорошая программа! Идеально!
Спасибо огромное за такой калькулятор. Все верно и подробно рассчитал. Я очень довольна.
Спасибо большое, очень помогли. Развивайтесь дальше. И сделайте расчёт рамы.
Супер, отличный способ проверить себя, если не совсем уверен в своих расчётах. Спасибо разработчикам.
Шикарная работа, спасибо ребят! Добавьте скорее рамы)
Спасибо, вы очень помогли, хорошая программа!
Спасибо огромное, все понятно и даже начала понимать, что откуда берется.
Спасибо большое! Очень помогли, сайт просто замечательный)
Удобный интерфейс, бесплатный сервис, идеальный сайт. Использую для проверки решенных задач)
Очень крутой сервис, техподдержка порадовала!
Очень крутой сайт, решения выдает правильные и подробные, если что то не получается, то подсказывает очень приятный собеседник, сайт такой 1 на миллион, очень круто сделали!! ♥♥♥
Очень хороший калькулятор) Я даже начал понимать как делать самому) не хватает очень трапециевидной нагрузки, пришлось самому думать как решить эту проблему) Ну, а так молодцы, так держать)
Шикарная программа! сделайте её на систему Windows Phone !