Содержание
Попробуйте растянуть воздушный шарик руками. В длину, в ширину. Прикиньте на глазок или замерьте расстояние, на которое вам удалось его растянуть. А теперь надуйте шарик.
И сравните длину и ширину надутого шарика с тем расстоянием, на которое вам удавалось его растянуть. Практически в ста процентах случаев оказывается, что воздух, самый обыкновенный воздух, которым вы дышите, справился значительно лучше ваших мышц. Поразительно, не правда ли? Точно так же мы накачиваем камеры машин и велосипедов, мячи для спортивных игр, и после качественной накачки мы абсолютно не в состоянии сжать руками воздух внутри камеры или мяча. Отчего так происходит? Почему воздух оказывается намного сильнее нас, не имея ни мускулов, ни приспособлений для этого? Это явление носит название давление газа и проходится в седьмом классе на уроках физики.
Давление газа в физике
Абсолютно все вещества состоят из мельчайших, не видимых глазу частиц – молекул. Эти молекулы находятся в беспрерывном хаотичном движении. И если в твердых телах это лишь небольшое колебание на одном месте, то в жидкостях и газах это движение происходит в любых направлениях, молекулы сталкиваются друг с другом, летят в новом направлении, вновь сталкиваются и так далее, рисуя немыслимые траектории и пересекая неисчислимое расстояние. Удар при столкновении одной молекулы очень и очень мал, но, как известно, молекул невероятное множество, двигаются они очень быстро, а потому действие всех молекул – это довольно значительная величина. То есть, многочисленные удары беспорядочно движущихся молекул и создают давление газа на стенки сосуда или на помещенное в газ тело.
Именно потому, когда мы надували воздушный шарик, мы наполняли его все новыми и новыми порциями воздуха, то есть газа, и, будучи накачиваемым все в большем количестве, он создавал все большее давление на стенки шарика, растягивая его. А так как из-за хаотического движения молекулы равномерно распределяются по всему объему, создавая равномерное давление газа на стенки сосуда, то и шарик равномерно раздувался во все стороны.
Зависимость давления газа от температуры
Если же мы уменьшаем объем сосуда при постоянной массе и температуре газа, то его давление на стенки уменьшается. Это и понятно, так как при увеличении объема расстояние между молекулами становится больше и количество соударений уменьшается. Существует также зависимость давления газа от температуры. Чем выше температура, тем выше скорость молекул газа и, соответственно, количество соударений и их сила увеличивается. Поэтому категорически нельзя нагревать баллоны со сжиженным газом, так как от увеличения давления внутри они могут не выдержать и взорваться. Для измерения давления газа существуют специальные приборы, самый известный из которых – это барометр, который позволяет нам узнать величину атмосферного давления и, исходя их этих данных, одеваться на улицу соответственно.
Нужна помощь в учебе?
Предыдущая тема: Способы уменьшения и увеличения давления
Следующая тема:   Закон Паскаля: формула и применение
|
Все неприличные комментарии будут удаляться. 2) Давле́ние в физике — отношение силы, нормальной к поверхности взаимодействия между телами, к площади этой поверхности или в виде формулы: P = F/S 3) Увелечение или уменьшение поверхности тела 4) Давление газа – это результат многочисленных столкновений между молекулами газа и стенками сосуда, в котором он содержится Разделив левую и правую части уравнения (4.4.8) на SΔt и учитывая соотношение (4.3.6), найдем давление газа Это и есть основное уравнение молекулярно-кинетической теории идеального газа*. * Это уравнение — первое количественное соотношение, полученное в молекулярно-кинетической теории. Поэтому его принято называть основным. Давление идеального газа пропорционально произведению массы молекулы на концентрацию молекул и средний квадрат их скорости. Формула (4.4.9) связывает макроскопическую величину — давление, которое может быть измерено манометром, — с микроскопическими величинами, характеризующими молекулы, и является как бы мостом между двумя мирами: макроскопическим и микроскопическим. Если через Отметим в заключение, что хотя расчет произведен без явного учета столкновений молекул, это не означает, что столкновения совсем не учитывались нами. Именно огромное число столкновений приводит к тому, что движение молекул является хаотическим. Равенства (4.3.4) и (4.3.6) выполняются с большой точностью как раз вследствие громадного числа столкновений. Нам удалось вычислить давление идеального газа на стенки сосуда. Оно зависит от концентрации молекул. Кроме того, давление газа пропорционально средней кинетической энергии молекул. Это и есть главный факт. § 4.5. Температура— мера средней кинетической энергии молекулИз основного уравнения молекулярно-кинетической теории газа вытекает важное следствие: температура есть мера средней кинетической энергии молекул. Докажем это. Для простоты будем считать количество газа равным 1 моль. Молярный объем газа обозначим через VM. Произведение молярного объема на концентрацию молекул представляет собой постоянную Авогадро NA, т. е. число молекул в 1 моль. Формула (4.5.1) устанавливает связь макроскопических параметров — давления р и объема VM — со средней кинетической энергией поступательного движения молекул. Вместе с тем полученное опытным путем уравнение состояния идеального газа для 1 моль имеет вид: Левые части уравнений (4.5.1) и (4.5.2) одинаковы, значит, должны быть равны и их правые части, т. е.
Отсюда вытекает связь между средней кинетической энергией поступательного движения молекул и температурой: Средняя кинетическая энергия хаотического движения молекул газа пропорциональна абсолютной температуре. Чем выше температура, тем быстрее движутся молекулы. Соотношение между температурой и средней кинетической энергией поступательного движения молекул (4.5.3) установлено для разреженных газов. Однако оно оказывается справедливым для любых веществ, движение атомов или молекул которых подчиняется законам механики Ньютона. Оно верно для жидкостей, а также для твердых тел, у которых атомы могут лишь колебаться возле положений равновесия в узлах кристаллической решетки. При приближении температуры к абсолютному нулю энергия теплового движения молекул также приближается к нулю*. * При очень низких температурах (вблизи абсолютного нуля) движение атомов и молекул уже не подчиняется законам Ньютона. Согласно более точным законам движения микрочастиц — законам квантовой механики — абсолютный нуль соответствует минимальному значению энергии движения, а не полному прекращению какого-либо движения вообще. |
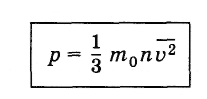(4.4.9)
обозначить среднюю кинетическую энергию поступательного движения молекулы: 
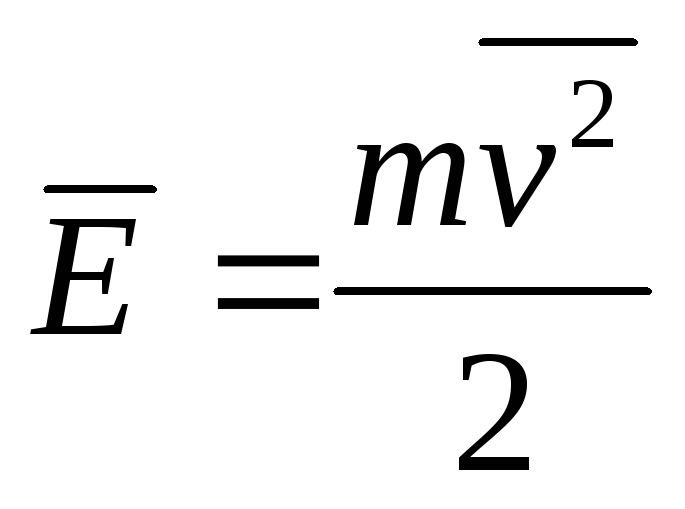, то уравнение (4.4.9) можно записать в форме:
(4.4.10)
(4.5.1)
(4.5.2)
(4.5.3)