Для определения скоростей и расходов жидкостей в промышленной практике обычно применяются дроссельные приборы и пневмометрические трубки.
Принцип работы пневмометрических трубок, например трубки Пито–Прандтля, мы рассматривали при выводе уравнения Бернулли (рис. 6-1). В каждом сечении разность уровней жидкости в трубках, изображенных на рисунке, выражает скоростной напор  в точке сечения, лежащей на оси трубы.
в точке сечения, лежащей на оси трубы.
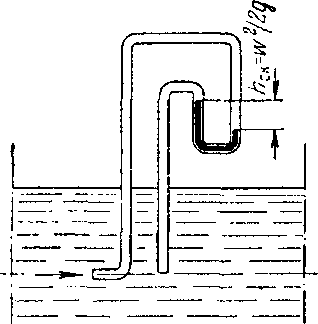
Рис. 6-2. Измерение скорости жидкости пневмометрической трубкой.
Разность уровней рабочей жидкости в трубках удобнее измерять не посредством пьезометрических трубок, как показано на рис. 6-1, а при помощи дифференциального манометра (рис. 6-2). Его U-образная трубка заполнена жидкостью, которая не смешивается с рабочей и имеет значительно большую плотность, чем последняя (например, вода или спирт – при работе с газами или ртуть – при работе с капельными жидкостями). Это позволяет измерять перепады давлений в случае значительного избыточного давления (или вакуума) в трубопроводе при относительно небольшой высоте прибора.
По результатам измерений 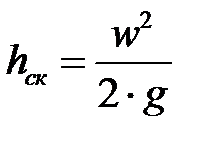 находят максимальную скорость жидкости вдоль оси трубопровода. Для определения средней скорости жидкости либо снимают эпюру распределения скоростей по сечению трубопровода, передвигая пневмометрическую трубку в различные точки сечения, либо используют соотношения между средней и максимальной, скоростями при ламинарном и турбулентном режимах течения. Расход жидкости находят, умножая среднюю скорость на площадь поперечного сечения трубопровода.
находят максимальную скорость жидкости вдоль оси трубопровода. Для определения средней скорости жидкости либо снимают эпюру распределения скоростей по сечению трубопровода, передвигая пневмометрическую трубку в различные точки сечения, либо используют соотношения между средней и максимальной, скоростями при ламинарном и турбулентном режимах течения. Расход жидкости находят, умножая среднюю скорость на площадь поперечного сечения трубопровода.
Такой способ определения скорости и расхода жидкости прост, но недостаточно точен из-за трудности установки пневмометрических трубок строго вдоль оси трубопровода.
Более широко распространено определение скоростей и расходов жидкостей с помощью дроссельных приборов, принцип работы которых основан на измерении перепада давлений при изменении поперечного сечения трубопровода. При искусственном сужении сечения потока посредством дроссельного прибора скорость и, соответственно, кинетическая энергия потока в этом более узком сечении возрастают, что приводит к уменьшению потенциальной энергии давления в том же сечении. Поэтому, измерив дифференциальным манометром перепад давлений между сечением трубопровода до его сужения и сечением в самом сужении (или вблизи него), можно вычислить изменение скорости между сечениями, а по нему – скорость и расход жидкости.
В качестве дроссельных приборов используют мерные диафрагмы, сопла и трубы Вентури.
Мерная диафрагма (рис. II-17) представляет собой тонкий диск с отверстием круглого сечения, центр которого расположен на оси трубы. Мерное сопло (рис. 6-3) является насадком, имеющим плавно закругленный вход и цилиндрический выход. Дифманометры мерных сопел (а также диафрагм) присоединяют к трубопроводу через кольцевые камеры а, соединенные с внутренним пространством трубопровода отверстиями, равномерно расположенными по окружности, или двумя каналами.

Рис. 6.3 – Мерная диафрагма

Рис. 6-4. Мерное сопло.

Рис. 6.5 Труба Вентури
Труба Вентури (рис. 6-5) имеет постепенно сужающееся сечение, которое затем расширяется до первоначального размера. Вследствие такой формы трубы Вентури потеря давления в ней меньше, чем в диафрагмах или соплах. Вместе с тем длина трубы Вентури очень велика по сравнению с толщиной диафрагмы или сопла, которые могут быть установлены между фланцами трубопровода.
В трубе Вентури и в сопле площадь сечения сжатой струи 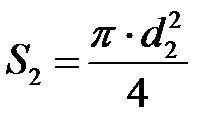 равна площади самого отверстия
равна площади самого отверстия 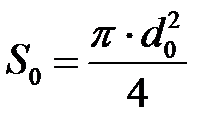 (
( 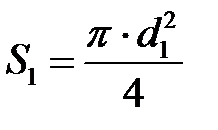 – площадь сечения трубопровода, на котором установлен дроссельный прибор).
– площадь сечения трубопровода, на котором установлен дроссельный прибор).
В диафрагме  (см. рис. 6-4).
(см. рис. 6-4).
Считая трубопровод горизонтальным, запишем для двух сечений, перепад давлений между которыми измеряется дифференциальным манометром, уравнение Бернулли. В соответствии с обозначениями на рис. 6-4 и пренебрегая потерей напора, имеем
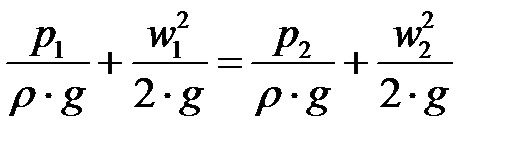
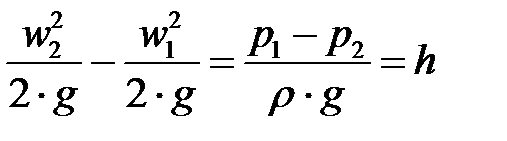
Где 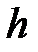 – перепад (разность) давлений, измеряемый дифференциальным манометром и выражаемый в метрах столба рабочей жидкости.
– перепад (разность) давлений, измеряемый дифференциальным манометром и выражаемый в метрах столба рабочей жидкости.
Чтобы определить среднюю скорость и расход жидкости в трубопроводе, выразим скорость  в сечении трубы через скорость
в сечении трубы через скорость  в узком сечении струи за диафрагмой, в котором замеряется давление
в узком сечении струи за диафрагмой, в котором замеряется давление 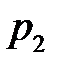 , пользуясь уравнением неразрывности потока
, пользуясь уравнением неразрывности потока
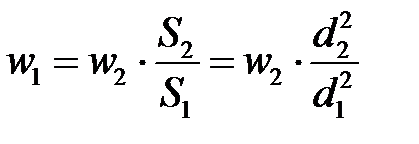
Подставим значение 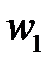 в выражение разности скоростных напоров
в выражение разности скоростных напоров
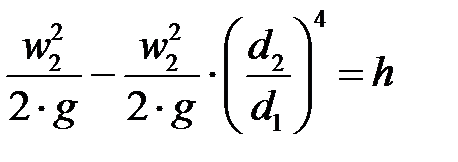
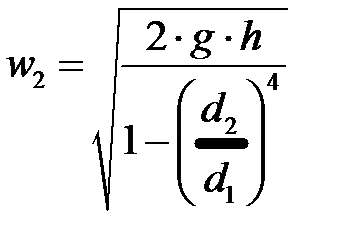
Объемный расход жидкости Q в сечении  отверстия диафрагмы (а значит, и в трубопроводе) будет равен
отверстия диафрагмы (а значит, и в трубопроводе) будет равен
 |
6-5 |
где 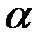 – поправочный коэффициент (
– поправочный коэффициент ( 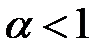 ); этим коэффициентом учитывается уменьшение скорости
); этим коэффициентом учитывается уменьшение скорости 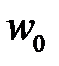 в сечении
в сечении 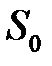 по сравнению со скоростью
по сравнению со скоростью 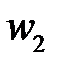 из-за сужения струи (
из-за сужения струи ( 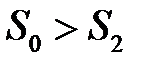 ), а также потеря напора в диафрагме.
), а также потеря напора в диафрагме.
Коэффициент 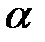 называется коэффициентом расхода дроссельного прибора. Его значение зависит от значения критерия Рейнольдса для жидкости и от отношения диаметра отверстия дроссельного прибора к диаметру трубопровода:
называется коэффициентом расхода дроссельного прибора. Его значение зависит от значения критерия Рейнольдса для жидкости и от отношения диаметра отверстия дроссельного прибора к диаметру трубопровода:
 |
6-6 |
Значения 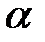 , определенные опытным путем, приводятся в специальной и справочной литературе.
, определенные опытным путем, приводятся в специальной и справочной литературе.
Диаметр дроссельного устройства обычно в 3–4 раза меньше диаметра трубопровода, поэтому величиной (d2/d1)i в уравнении (6-5) можно в первом приближении пренебречь и находить расход жидкости по уравнению
 |
6-7 |
Среднюю скорость жидкости в трубопроводе определяют, разделив Q на площадь сечения трубопровода. Опуская индексы «1» у 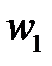 и
и  получим
получим
В случае работы со сжимаемыми жидкостями (газом или паром) при больших перепадах давлений в уравнения (6-5) и (5-8) вводят еще один поправочный коэффициент, учитывающий изменение плотности газа (пара).
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8461 –  | 7349 –
| 7349 –  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Гидродинамика – раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.
Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.
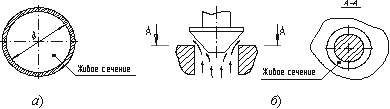
Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения. Например, живое сечение трубы – круг (рис.3.1, б); живое сечение клапана – кольцо с изменяющимся внутренним диаметром (рис.3.1, б).
Смоченный периметр χ ("хи") – часть периметра живого сечения, ограниченное твердыми стенками (рис.3.2, выделен утолщенной линией).
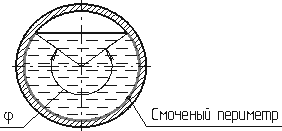
Для круглой трубы
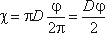
если угол в радианах, или
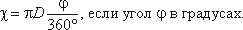
Расход потока Q – объем жидкости V, протекающей за единицу времени t через живое сечение ω.
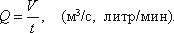
Средняя скорость потока υ – скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω
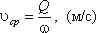
Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.
Гидравлический радиус потока R – отношение живого сечения к смоченному периметру
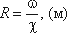
Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени
Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным
Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.
Трубка тока – трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное – течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.
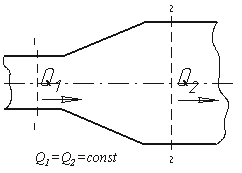
Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q1=Q2= const, откуда
Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:
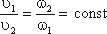
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.
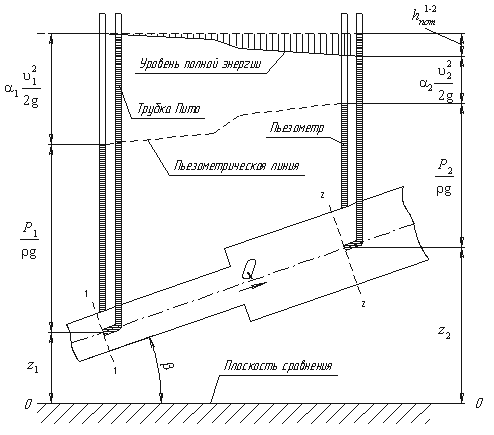
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).
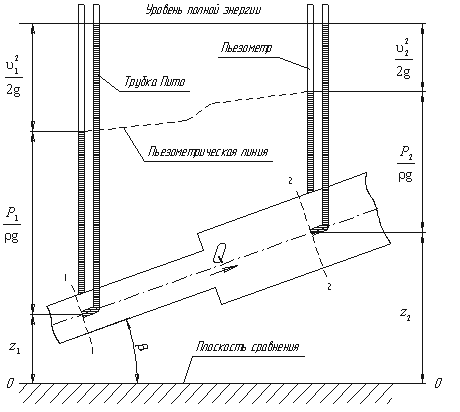
Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.
Для измерения давления жидкости применяют пьезометры – тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту 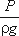 . В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.
. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.
Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).
Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.
Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.
Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:
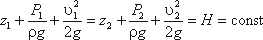
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:
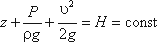
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.
С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:
z1 и z2 – удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2; 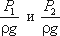 – удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
– удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях; 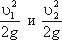 – удельные кинетические энергии в тех же сечениях.
– удельные кинетические энергии в тех же сечениях.
Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.
Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис.3.5, можно заметить, что z1 и z2 – геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения; 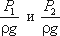 – пьезометрические высоты;
– пьезометрические высоты; 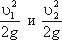 – скоростные высоты в указанных сечениях.
– скоростные высоты в указанных сечениях.
В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.
Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения
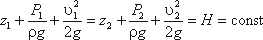
Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).
Потерянная энергия или потерянный напор обозначаются  и имеют также линейную размерность.
и имеют также линейную размерность.
Уравнение Бернулли для реальной жидкости будет иметь вид:
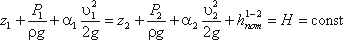
Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.
Кроме этого в уравнении появились еще два коэффициента α1 и α2, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).
Потерянная высота  складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)
складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим
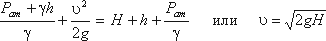
где Н – столб жидкости в трубке Пито.
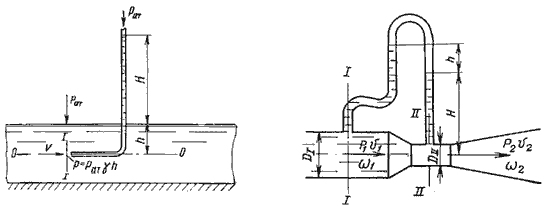
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.
Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:
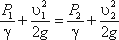
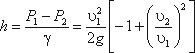
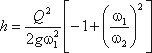
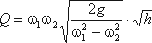
Выражение, стоящее перед 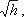 , является постоянной величиной, носящей название постоянной водомера Вентури.
, является постоянной величиной, носящей название постоянной водомера Вентури.
Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3), загнутый конец которой направлен навстречу потоку.
Трубка полного напора, или трубка Пито , служит для измерения скорости потока, например в трубе. Если установить в одном сечении потока трубку, изогнутую под углом 90, отверстием навстречу потоку и пьезометр, то жидкость в трубке поднимется над уровнем жидкости в пьезометре на высоту, равную скоростному напору. Объясняется это тем, что скорость частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, следовательно, давление увеличивается на величину скоростного напора. Измерив, разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке.
Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

где Н – столб жидкости в трубке Пито.

Рис. 3. Трубка Пито и pасходомер Вентури
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.
Расходомер Вентури представляет собой устройство, устанавливаемое в трубопроводах и осуществляющее сужение потока – дросселирование. Расходомер состоит из двух участков – плавно сужающегося (сопла) и постепенно расширяющегося (диффузора). Скорость потока в сужающемся месте возрастает, а давление падает. Возникает разность (перепад) давлений, которую можно измерить двумя пьезометрами или дифференциальным U-образным ртутным манометром.
Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:


Используя уравнение неразрывности
сделаем замену в получено выражении:

Решая относительно Q, получим

Выражение, стоящее перед 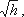 , является постоянной величиной, носящей название постоянной водомера Вентури.
, является постоянной величиной, носящей название постоянной водомера Вентури.
 Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.
Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.
Карбюратор поршневых двигателей внутреннего сгорания (рис.4) служит для подсоса бензина и смешивания его с потоком воздуха. Поток воздуха, засасываемого в двигатель, сужается в том месте (сечение 2-2), где установлен распылитель бензина (обрез трубки диаметром d). Скорость воздуха в этом сечении возрастает, а давление по закону Бернулли падает. Благодаря пониженному давлению бензин вытекает в поток воздуха.
Рис. 4. Схема карбюратора
 Струйный насос (эжектор) (рис.5) состоит из плавно сходящегося насадка 2, осуществляющего сжатие потока, и постепенно расширяющейся трубки 4, установленной на некотором расстоянии от насадка в камере 3. Вследствие увеличения скорости потока давление в струе потока на выходе насадка 2 и во всей камере 3 значительно понижается. В расширяющейся трубке 4 скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в атмосферу). Следовательно, в камере 3 давление обычно меньше атмосферного, т.е. в ней имеется разрежение (вакуум). Под действием разрежения жидкость из нижнего резервуара всасывается по трубе 1 в камеру 3, где происходит слияние и перемешивание двух потоков.
Струйный насос (эжектор) (рис.5) состоит из плавно сходящегося насадка 2, осуществляющего сжатие потока, и постепенно расширяющейся трубки 4, установленной на некотором расстоянии от насадка в камере 3. Вследствие увеличения скорости потока давление в струе потока на выходе насадка 2 и во всей камере 3 значительно понижается. В расширяющейся трубке 4 скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в атмосферу). Следовательно, в камере 3 давление обычно меньше атмосферного, т.е. в ней имеется разрежение (вакуум). Под действием разрежения жидкость из нижнего резервуара всасывается по трубе 1 в камеру 3, где происходит слияние и перемешивание двух потоков.
Рис. 5. Схема струйного насоса (эжектора):
1 — труба; 2 — насадок; 3 — камера; 4 — расширяющаяся трубка
Практическая работа №5.
Тема:Режимы движения жидкости.
Цель работы: Ознакомиться с режимами движения жидкости и опытом Рейнольдса.
1. Записать определение ламинарного режима течения.
2. Записать определение турбулентного режима течения.
3. Зарисовать экспериментальную установку О.Рейнольдса и описать опыт.
4. Определить число Рейнольдса и режим движения воды в водопроводной трубе d мм, если расход воды Qм 3 /с.
Температура воды t 0 С.
5. Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр dminмм максимальный диаметр dmaxмм. Расчётные скорости движения воды в них v1…v2 м/с. Определить минимальное и максимальное числа Рейнольдса и режим течения воды в этих трубопроводах.
| Вариант | d мм | Qм 3 /с | t 0 С | dminмм | dmaxмм | v1 м/с | v2 м/с |
| 1. | 0,132 | 0,4 | 3,7 | ||||
| 2. | 0,134 | 0,5 | 3,8 | ||||
| 3. | 0,138 | 0,6 | 3,9 | ||||
| 4. | 0,132 | 0,7 | 4,0 | ||||
| 5. | 0,134 | 0,8 | 4,2 | ||||
| 6. | 0,138 | 0,4 | 4,3 | ||||
| 7. | 0,142 | 0,5 | 4,1 | ||||
| 8. | 0,132 | 0,6 | 4,5 | ||||
| 9. | 0,134 | 0,7 | 3,7 | ||||
| 10. | 0,138 | 0,8 | 3,8 | ||||
| 11. | 0,142 | 0,4 | 3,9 | ||||
| 12. | 0,132 | 0,5 | 4,0 | ||||
| 13. | 0,134 | 0,6 | 4,2 | ||||
| 14. | 0,138 | 0,7 | 4,3 | ||||
| Вариант | Qм 3 /с | t 0 С | dminмм | dmaxмм | v1 м/с | v2 м/с | |
| 15. | 0,132 | 0,4 | 3,7 | ||||
| 16. | 0,134 | 0,5 | 3,8 | ||||
| 17. | 0,138 | 0,6 | 3,9 | ||||
| 18. | 0,142 | 0,7 | 4,0 | ||||
| 19. | 0,132 | 0,8 | 4,2 | ||||
| 20. | 0,134 | 0,4 | 4,3 | ||||
| 21. | 0,138 | 0,5 | 4,1 | ||||
| 22. | 0,142 | 0,6 | 4,5 | ||||
| 23. | 0,132 | 0,7 | 3,7 | ||||
| 24. | 0,134 | 0,8 | 3,8 | ||||
| 25. | 0,138 | 0,4 | 3,9 | ||||
| 26. | 0,142 | 0,5 | 4,0 | ||||
| 27. | 0,132 | 0,6 | 4,2 | ||||
| 28. | 0,134 | 0,7 | 4,3 | ||||
| 29. | 0,138 | 0,8 | 4,1 | ||||
| 30. | 0,142 | 0,4 | 4,5 | ||||
| 31. | 0,132 | 0,5 | 3,7 |
6. Вывод по работе.
Контрольные вопросы:
1. Дайте определение ламинарного режима течения.
2. Дайте определение турбулентного режима течения.
3. Перечислите факторы, от которых зависит характер течения жидкости.
4. В чем заключается физический смысл числа Рейнольдса.
5. Что означает критическое число Рейнольдс

