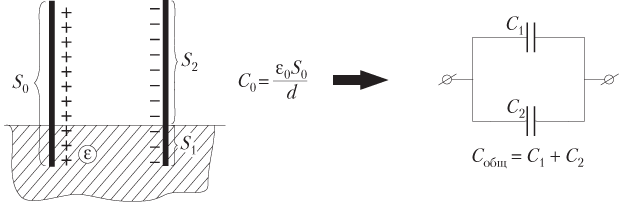Два плоских конденсатора ёмкостью С и 2С соединили параллельно и зарядили до напряжения U. Затем ключ К разомкнули, отключив конденсаторы от источника (см. рисунок). Пространство между их обкладками заполнено жидким диэлектриком с диэлектрической проницаемостью ε. Какой будет разность потенциалов между обкладками, если из левого конденсатора диэлектрик вытечет?
В соответствии с определением понятия «ёмкость» для суммарного заряда конденсаторов имеем:
где 3С — суммарная ёмкость конденсаторов, когда оба они заполнены жидким диэлектриком. После вытекания диэлектрика из левого конденсатора суммарный заряд останется прежним. Так как для плоского конденсатора C
ε, то суммарная ёмкость станет равной (С/ε + 2С), а напряжение будет равно U1, так что
Решая систему уравнений (1) и (2), получим ответ:
Ответ:
Два одинаковых плоских конденсатора, соединенных параллельно, зарядили до напряжения В и отключили от источника. Затем пластины одного из конденсаторов раздвинули так, что расстояние между ними увеличилось в раза. После этого пластины конденсатора замкнули проводником. Какая энергия выделилась в проводнике? Первоначальная емкость каждого конденсатора пФ.
Соединенные параллельно конденсаторы образуют батарею емкостью , полный заряд на которой равен . Поскольку после зарядки конденсаторов батарею отключили от источника, суммарный заряд на ней остается постоянным. Учитывая, что емкость плоского конденсатора обратно пропорциональна расстоянию между пластинами, найдем емкость батареи после раздвигания пластин одного из конденсаторов: . За счет работы, совершенной при раздвигании пластин, энергия батареи возрастает и принимает значение . При замыкании пластин эта энергия выделится в проводнике. Ответ: Дж.
Емкость конденсатора можно изменить, увеличивая или уменьшая расстояние между его обкладками, заменяя диэлектрик в пространстве между ними и т.п. При этом определяющим оказывается, отключен или подключен конденсатор к источнику напряжения.
Если конденсатор (или батарея конденсаторов):
- подключен к источнику напряжения, то разность потенциалов (напряжение) между обкладками конденсатора сохраняется неизменной и равной напряжению на полюсах источника:
- отключен от источника напряжения, то заряд на обкладках конденсатора остается неизменным:
При соединении между собой одноименных обкладок двух заряженных конденсаторов имеет место их параллельное соединение .
Параметры такой батареи конденсаторов вычисляются следующим образом:
- напряжение на батарее конденсаторов
где Q общ — заряд батареи конденсаторов; C общ — электроемкость батареи;
- электроемкость батареи конденсаторов
C общ = C 1 + C 2 ,
где С 1 — электроемкость первого конденсатора; С 2 — электроемкость второго конденсатора;
Q общ = Q 1 + Q 2 ,
где Q 1 — начальный заряд первого конденсатора, Q 1 = C 1 U 1 ; U 1 — напряжение (разность потенциалов) между обкладками первого конденсатора до соединения; Q 2 — начальный заряд второго конденсатора, Q 2 = C 2 U 2 ; U 2 — напряжение (разность потенциалов) между обкладками второго конденсатора до соединения.
При соединении между собой разноименных обкладок двух заряженных конденсаторов имеет место (как и в случае соединения одноименных обкладок) их параллельное соединение .
Параметры такой батареи конденсаторов вычисляются следующим образом:
- напряжение на батарее конденсаторов
где Q общ — заряд батареи конденсаторов; C общ — емкость батареи;
- электроемкость батареи конденсаторов
C общ = C 1 + C 2 ,
где C 1 — электроемкость первого конденсатора; C 2 — электроемкость второго конденсатора;
Q общ = | Q 1 − Q 2 |,
где Q 1 — начальный заряд первого конденсатора, Q 1 = C 1 U 1 ; U 1 — напряжение (разность потенциалов) между обкладками первого конденсатора до соединения; Q 2 — начальный заряд второго конденсатора, Q 2 = C 2 U 2 ; U 2 — напряжение (разность потенциалов) между обкладками второго конденсатора до соединения.
Пример 17. Два конденсатора одинаковой электроемкости заряжены до разности потенциалов 120 и 240 В соответственно, а затем соединены одноименно заряженными пластинами. Какова станет разность потенциалов между обкладками конденсаторов после указанного соединения?
Решение . До соединения одноименных пластин конденсаторов каждый из них обладал зарядом:
Q 1 = C 1 U 1 = CU 1 ,
где C 1 — электроемкость первого конденсатора, C 1 = C ; U 1 — разность потенциалов между обкладками первого конденсатора;
Q 2 = C 2 U 2 = CU 2 ,
где C 2 — электроемкость второго конденсатора, C 2 = C ; U 2 — разность потенциалов между обкладками второго конденсатора.
При соединении одноименных обкладок получим параллельное соединение конденсаторов. Разность потенциалов между обкладками батареи конденсаторов определяется формулой
где Q общ — общий заряд батареи; C общ — общая электроемкость батареи.
Общий заряд батареи двух конденсаторов, полученной соединением их одноименных обкладок, определяется суммой зарядов каждого из них:
Q общ = Q 1 + Q 2 ,
а общая электроемкость батареи двух одинаковых конденсаторов, соединенных параллельно, —
C общ = C 1 + C 2 = 2 C .
Следовательно, разность потенциалов между обкладками батареи определяется выражением
U = Q общ C общ = Q 1 + Q 2 2 C = C U 1 + C U 2 2 C = U 1 + U 2 2 .
U = 120 + 240 2 = 180 В.
Разность потенциалов между обкладками конденсаторов после указанного соединения составит 180 В.
Пример 18. Два одинаковых плоских конденсатора заряжены до разности потенциалов 200 и 300 В. Определить разность потенциалов между обкладками конденсаторов после соединения их разноименных обкладок.
Решение . До соединения разноименных пластин конденсаторов каждый из них обладал зарядом:
Q 1 = C 1 U 1 = CU 1 ,
где C 1 — электроемкость первого конденсатора, C 1 = C ; U 1 — разность потенциалов между обкладками первого конденсатора;
Q 2 = C 2 U 2 = CU 2 ,
где C 2 — электроемкость второго конденсатора, C 2 = C ; U 2 — разность потенциалов между обкладками второго конденсатора.
При соединении разноименных обкладок получаем параллельное соединение конденсаторов. Разность потенциалов между обкладками батареи конденсаторов определяется формулой
где Q общ — общий заряд батареи; C общ — общая электроемкость батареи.
Общий заряд батареи двух конденсаторов, полученной соединением их разноименных обкладок, определяется модулем разности зарядов каждого из них:
Q общ = | Q 1 − Q 2 |,
а общая электроемкость батареи двух одинаковых конденсаторов, соединенных параллельно, —
C общ = C 1 + C 2 = 2 C .
Следовательно, разность потенциалов между обкладками батареи определяется выражением
U = Q общ C общ = | Q 1 − Q 2 | 2 C = | C U 1 − C U 2 | 2 C = | U 1 − U 2 | 2 .
U = | 200 − 300 | 2 = 50 В.
Разность потенциалов между обкладками конденсаторов после указанного соединения составит 50 В.
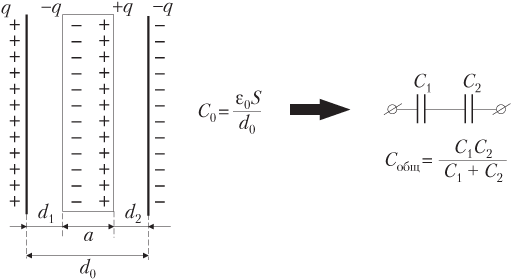
Пример 19. Плоский воздушный конденсатор заряжен до 180 В и отключен от источника напряжения. В пространство между его обкладками, параллельно им, вводят незаряженную металлическую пластину, толщина которой в 3 раза меньше расстояния между обкладками. Считая, что металлическая пластина расположена симметрично относительно обкладок конденсатора, определить разность потенциалов, которая установится между ними.
Решение . При помещении металлической пластины в плоский конденсатор так, как показано на рисунке, свободные электроны в металле перераспределяются:
- плоскость, обращенная к положительно заряженной обкладке конденсатора, получает избыток электронов и заряжается отрицательным зарядом q 1 = − q ;
- плоскость, обращенная к отрицательно заряженной обкладке конденсатора, имеет недостаток электронов и заряжается положительным зарядом q 2 = + q .
В результате перераспределения заряда пластина остается нейтральной:
Q = q 1 + q 2 = − q + q = 0.
Перераспределение заряда в металлической пластине приводит к образованию батареи двух конденсаторов:
- положительно заряженная обкладка конденсатора и отрицательно заряженная плоскость металлической пластины имеют одинаковые по модулю заряды противоположного знака; они могут рассматриваться как конденсатор с электроемкостью
где ε 0 — электрическая постоянная, ε 0 = 8,85 ⋅ 10 −12 Кл 2 /(Н ⋅ м 2 ); S — площадь обкладки конденсатора; d 1 — расстояние между положительно заряженной обкладкой конденсатора и отрицательно заряженной плоскостью металлической пластины;
- отрицательно заряженная обкладка конденсатора и положительно заряженная плоскость металлической пластины также имеют одинаковые по модулю заряды противоположного знака; они могут рассматриваться как конденсатор с электроемкостью
где d 2 — расстояние между отрицательно заряженной обкладкой конденсатора и положительно заряженной плоскостью металлической пластины.
Оба конденсатора имеют одинаковые заряды и образуют последовательное соединение. Электроемкость батареи двух конденсаторов при последовательном соединении определяется формулой
1 C общ = 1 C 1 + 1 C 2 , или C общ = C 1 C 2 C 1 + C 2 .
При симметричном расположении пластины в пространстве между обкладками конденсатора ( d 1 = d 2 = d ) электроемкости конденсаторов одинаковы:
C 1 = C 2 = ε 0 S d ,
общая электроемкость батареи задается выражением
C общ = C 1 C 2 C 1 + C 2 = C 2 = ε 0 S 2 d ,
где d = ( d 0 − a )/2; d 0 — расстояние между обкладками конденсатора до введения пластины; a — толщина металлической пластины.
Разность потенциалов между обкладками батареи
U = Q общ C общ = 2 d q ε 0 S = q ( d 0 − a ) ε 0 S ,
где Q общ — заряд батареи последовательно соединенных конденсаторов, Q общ = q .
Первоначальная разность потенциалов определяется формулой
U 0 = Q 0 C 0 = Q 0 d 0 ε 0 S ,
где Q 0 — заряд конденсатора до введения пластины, Q 0 = q (конденсатор отключен от источника напряжения); C 0 — электроемкость конденсатора до введения пластины.
Отношение разности потенциалов до и после введения металлической пластины определяется выражением
U U 0 = d 0 − a d 0 .
Отсюда найдем искомую разность потенциалов
U = U 0 d 0 − a d 0 .
С учетом d 0 = 3 a выражение принимает вид:
U = U 0 3 a − a 3 a = 2 3 U 0 .
U = 2 3 ⋅ 180 = 120 В.
В результате введения в конденсатор металлической пластины разность потенциалов между его обкладками уменьшилась и составила 120 В.
Пример 20. Плоский воздушный конденсатор заряжен до 240 В и отключен от источника напряжения. Его вертикально погружают в некоторую жидкость с диэлектрической проницаемостью 2,00 на одну треть объема. Найти разность потенциалов, которая установится между обкладками конденсатора.
Решение . При частичном погружении плоского воздушного конденсатора в жидкий диэлектрик, как показано на рисунке, свободные электроны на его обкладках перераспределяются таким образом, что:
- часть обкладок конденсатора, погруженная в диэлектрик, имеет заряд q 1 ;
- часть обкладок конденсатора, оставшаяся в воздухе, имеет заряд q 2 .
В результате перераспределения заряда по площади обкладок конденсатора на его обкладках устанавливается заряд:
Q общ = q 1 + q 2 .
Площадь обкладок конденсатора при частичном погружении его в жидкий диэлектрик разделяется на две части:
- часть, погруженная в диэлектрик, имеет площадь S 1 ; соответствующая часть конденсатора может рассматриваться как отдельный конденсатор с электроемкостью
C 1 = ε 0 ε S 1 d ,
где ε 0 — электрическая постоянная, ε 0 = 8,85 ⋅ 10 −12 Кл 2 /(Н ⋅ м 2 ); ε — диэлектрическая проницаемость конденсатора; d — расстояние между обкладками конденсатора;
- часть, оставшаяся в воздухе, имеет площадь S 2 ; соответствующая часть конденсатора может рассматриваться как отдельный конденсатор с электроемкостью
Оба конденсатора обладают одинаковой разностью потенциалов между обкладками и образуют параллельное соединение. Электроемкость батареи двух конденсаторов при параллельном соединении определяется формулой
C общ = C 1 + C 2 = ε 0 ε S 1 d + ε 0 S 2 d = ε 0 d ( ε S 1 + S 2 ) ,
а заряд на обкладках батареи —
Q общ = C общ U = ε 0 d ( ε S 1 + S 2 ) U ,
где U — разность потенциалов между обкладками батареи.
Электроемкость конденсатора до погружения его в диэлектрик определяется выражением
а заряд на его обкладках —
Q 0 = C 0 U 0 = ε 0 S 0 d U 0 ,
где U 0 — разность потенциалов между обкладками конденсатора до введения пластины; S 0 — площадь обкладки.
Конденсатор отключен от источника напряжения, поэтому его заряд после частичного погружения в диэлектрик не изменяется:
или, в явном виде,
ε 0 S 0 d U 0 = ε 0 d ( ε S 1 + S 2 ) U .
После упрощения имеем:
S 0 U 0 = (ε S 1 + S 2 ) U .
Отсюда следует, что искомая разность потенциалов определяется выражением
U = U 0 S 0 ε S 1 + S 2 .
С учетом того, что в диэлектрик погружена часть пластин конденсатора, т.е.
S 1 = η S 0 , S 2 = S 0 − S 1 = S 0 − η S 0 = S 0 (1 − η), η = 1 3 ,
U = U 0 S 0 ε η S 0 + S 0 ( 1 − η ) = U 0 ε η + 1 − η .
Отсюда найдем искомую разность потенциалов: