Напряженность магнитного полянеобходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах. Напряженность магнитного поля характеризует магнитное поле в вакууме.
Напряженность магнитного поля [H] – это отношение магнитной индукции к магнитной проницаемости среды
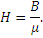
Напряженность магнитного поля – величина векторная. За единицу измерения напряженности магнитного поля в Международной системе единиц принят ампер на метр.
Напряженность магнитного поля (формула)векторная физическая величина, равная:
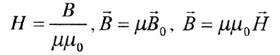
Напряженность магнитного поля в СИ – ампер на метр (А/м).
Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поляв данной точке, то можно определить индукцию поля в этой точке.
Напряженность магнитного поля зависит только от силы тока, протекающего по проводнику, и его геометрии.
Обобщая экспериментальные данные французских физиков Био и Савара, Лаплас (французский математик) предложил формулу, по которой можно вычислять напряженность поля, создаваемого элементом тока в точке, расположенной от этого элемента на расстоянии r.
- Теорема Ампера о циркуляции магнитного поля:
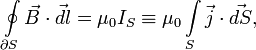
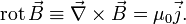
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9848 – 
| 7704 – 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
| Напряжённость магнитного поля | |
|---|---|
| H → <displaystyle <vec |
|
| Размерность | L −1 I |
| Единицы измерения | |
| СИ | А/м |
| СГС | Э |
| Примечания | |
| векторная величина | |
Напряжённость магни́тного по́ля — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M . Обычно обозначается символом Н .
H = 1 μ 0 B − M , <displaystyle mathbf
где μ 0 <displaystyle mu _<0>> — магнитная постоянная.
H = B − 4 π M . <displaystyle mathbf
В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот, намагниченность M зависит линейно от приложенного магнитного поля с индукцией B :
M = α B . <displaystyle mathbf
Однако исторически принято эту линейную зависимость описывать не коэффициентом α <displaystyle alpha > , а использовать связанные величины — магнитную восприимчивость χ <displaystyle chi > или магнитную проницаемость μ <displaystyle mu > :
M = χ 1 + 4 π χ B = μ − 1 4 π μ B . <displaystyle mathbf
В системе СГС напряжённость магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м). В технике эрстед постепенно вытесняется единицей СИ — ампером на метр.
1 Э = 1000/(4 π ) А/м ≈ 79,5775 А/м.
1 А/м = 4 π /1000 Э ≈ 0,01256637 Э.
Содержание
Физический смысл [ править | править код ]
В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряжённость магнитного поля ( Н ) совпадает с вектором магнитной индукции ( B ) с точностью до коэффициента, равного 1 в СГС и μ 0 <displaystyle mu _<0>> в СИ.
В магнетиках (магнитных средах) напряжённость магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как, например, в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».
Например, если поле создаётся катушкой с током, в которую вставлен железный сердечник, то напряжённость магнитного поля H внутри сердечника совпадает (в СГС точно, а в СИ — с точностью до постоянного размерного коэффициента) с вектором магнитной индукции B0 поля, которое было бы создано этой катушкой при отсутствии сердечника. B0 в принципе может быть рассчитан исходя из геометрии катушки и тока в ней, без всякой дополнительной информации о материале сердечника и его магнитных свойствах.
При этом надо иметь в виду, что более фундаментальной характеристикой магнитного поля является вектор магнитной индукции B . Именно он определяет силу действия магнитного поля на движущиеся заряженные частицы и токи, а также может быть непосредственно измерен, в то время как напряжённость магнитного поля H можно рассматривать скорее как вспомогательную величину (хотя рассчитать её, по крайней мере, в статическом случае, проще, в чём состоит её ценность: ведь H создает так называемые свободные токи, которые сравнительно легко непосредственно измерить, а трудно измеримые связанные токи — то есть токи молекулярные и т. п. — учитывать не надо).
Правда, в обычно используемое выражение для энергии магнитного поля (в среде) B и H входят почти равноправно, но надо иметь в виду, что в эту энергию включена и энергия, затраченная на поляризацию среды, а не только энергия собственно поля [1] . Энергия магнитного поля как такового выражается только через фундаментальную величину B . Тем не менее видно, что величина H феноменологическая и тут весьма удобна.
Если два параллельных проводника с током находятся в вакууме (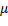 
= 1), то сила взаимодействия на единицу длины проводника, согласно (111.5), равна (112.1)
Для нахождения числового значения 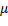0 воспользуемся определением ампера, согласно которому 
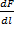= 2 • 10 -7 Н/м при I1 = I2 = 1 А и R — 1 м. Подставив это значение в (112.1), получим 
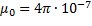Н/А 2 = 4 
Гн/м.
Единица индуктивности — генри (Гн) .
Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера запишется в виде dF = IBdl, откуда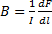 
Единица магнитной индукции —тесла (Тл): 1 Тл — магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику течет ток 1 А: 1 Тл=1Н/(А·м)
Так как 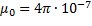Н/А 2 , а в случае вакуума ( 
), согласно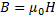 
, то для данного случая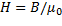 
Единица напряженности магнитного поля — ампер на метр (А/м): 1 А/м —напряженность такого поля, магнитная индукция которого в вакууме равна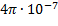 
Тл.
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
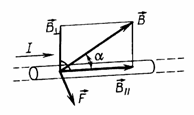Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником: F=BIℓsin a — закон Ампера.
Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током.
Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца:
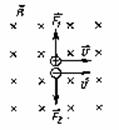
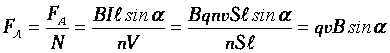
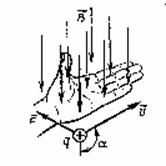Направление силы Лоренца (правило левой руки) Направление F определяется по правилу левой руки: вектор F перпендикулярен векторам В и v.
Правило левой руки сформулировано для положительной частицы. Сила, действующая на отрицательный заряд будет направлена в противоположную сторону по сравнению с положительным.
33. Магнитные силовые линии и магнитный поток. Работа магнитных сил. Теорема Гаусса для магнитного поля.
Линии магнитной индукции – линии, касательные к которым направлены также как и вектор магнитной индукции в данной точке поля. Магнитные поля, так же как и электрические, можно изображать графически при помощи линий магнитной индукции. Через каждую точку магнитного поля можно провести линию индукции. Так как индукция поля в любой точке имеет определённое направление, то и направление линии индукции в каждой точке данного поля может быть только единственным, а значит, линии магнитного поля, так же как и электрического поля, линии индукции магнитного поля прочерчивают с такой густотой, чтобы число линий, пересекающих единицу поверхности, перпендикулярной к ним, было равно (или пропорционально) индукции магнитного поля в данном месте. Поэтому, изображая линии индукции, можно наглядно представить, как меняется в пространстве индукция, а следовательно, и напряжённость магнитного поля по модулю и направлению.
Силовые линии электрических и магнитных полей – линии, касательные к которым в каждой точке поля совпадают с направлением напряженности электрического или соответствующего магнитного поля; качественно характеризуют распределение электромагнитного поля в пространстве. Силовые линии – только наглядный способ изображения силовых полей.
Направление линии магнитной индукции определяется по правилу правой руки (правило буравчика).
Линии магнитной индукции прямого проводника с током представляют концентрические окружности, лежащие в плоскости, перпендикулярной току.
Линии магнитной индукции всегда замкнуты и охватывают проводники с токами. Это отличает их от линий напряженности (силовых линий) электрического поля. Замкнутость линий магнитной индукции означает то, что в природе не существует магнитных зарядов.
В однородном магнитном поле, модуль вектора индукции которого равен В, помещен плоский замкнутый контур площадью S. Нормаль n к плоскости контура составляет угол α с направлением вектора магнитной индукции В.
Магнитным потоком через поверхность называется величина Ф, определяемая соотношением:
Единица измерения магнитного потока в системе СИ – 1 Вебер (1 Вб).
1 Вб = 1 Тл · 1 м 2
Магнитный поток через контур максимален, если плоскость контура перпендикулярна магнитному полю. Значит угол a равен 0 0 .
Тогда магнитный поток рассчитывается по формуле:
Магнитный поток через контур равен нулю, если контур располагается параллельно магнитному полю.
Значит угол α равен 90 0 .
Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю: (120.3)
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
Итак, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные выражения.
В качестве примера рассчитаем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью 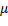, согласно (119.2), равна
Магнитный поток сквозь один виток соленоида площадью S равен а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,
Дата добавления: 2016-03-25 ; просмотров: 2516 | Нарушение авторских прав