Градиент потенциала электрического поля

Градиент потенциала – это скорость возрастания потенциала в направлении кротчайшем между двумя точками.

Между двумя точками имеется некоторая разность потенциалов. Если эту разность разделить на кратчайшее расстояние между взятыми точками, то полученное значение будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками.

Градиент потенциала показывает направление наибольшего возрастания потенциала, численно равен модулю напряженности и отрицательно направлен по отношению к нему.

В определении градиента существенны два положения:

1) Направление, в котором берутся две близлежащие точки, должно быть таким, чтобы скорость изменения была максимальной.

2) Направление таково, что скалярная функция в этом направлении возрастает.

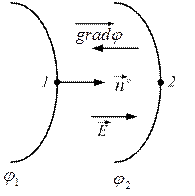
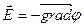
Для декартовой системы координат:

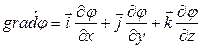
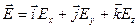
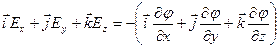
Скорость изменения потенциала в направлении оси Х, Y, Z:

; ;

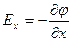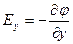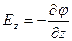
Два вектора равны только тогда, когда равны друг другу их проекции. Проекция вектора напряженности на ось Х равна проекции скорости изменения потенциала вдоль оси Х, взятой с обратным знаком. Аналогично для осей Y и Z.

; ; .

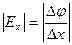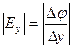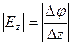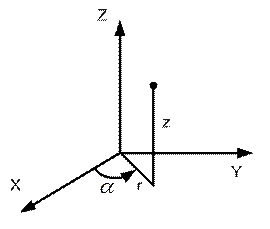
В цилиндрической системе координат выражение градиента потенциала будет иметь следующий вид:

.

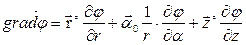А в сферической системе координат:

.

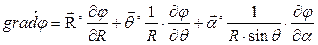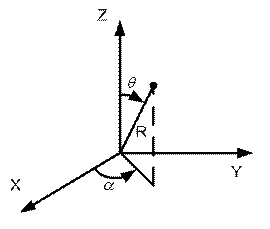
Дифференциальный оператор Гамильтона (оператор Набла)

Для сокращения записи операций над скалярными и векторными величинами употребляют дифференциальный оператор Гамильтона или оператор Набла:

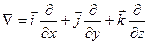
Под дифференциальным оператором Гамильтона понимают сумму частных производных по 3-м координатным осям, умноженных на соответствующие единичные векторы (орты).

Применим оператор Гамильтона к потенциалу:

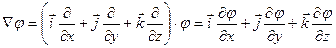
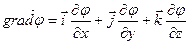
Правые части одинаковы, значит, будут одинаковы и левые части:

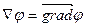
Оператор Гамильтона сочетает в себе как векторные, так и скалярные свойства и может быть применен к скалярным и векторным функциям.

Дата добавления: 2015-07-30 ; просмотров: 11000 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Градиент потенциала – это скорость возрастания потенциала в направлении кротчайшем между двумя точками.

Между двумя точками имеется некоторая разность потенциалов. Если эту разность разделить на кратчайшее расстояние между взятыми точками, то полученное значение будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками.

Градиент потенциала показывает направление наибольшего возрастания потенциала, численно равен модулю напряженности и отрицательно направлен по отношению к нему.

В определении градиента существенны два положения:

1) Направление, в котором берутся две близлежащие точки, должно быть таким, чтобы скорость изменения была максимальной.

2) Направление таково, что скалярная функция в этом направлении возрастает.

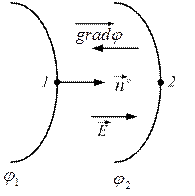
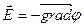
Для декартовой системы координат:

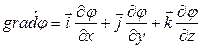
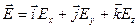
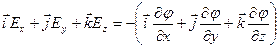
Скорость изменения потенциала в направлении оси Х, Y, Z:

; ;

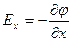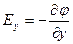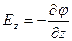
Два вектора равны только тогда, когда равны друг другу их проекции. Проекция вектора напряженности на ось Х равна проекции скорости изменения потенциала вдоль оси Х, взятой с обратным знаком. Аналогично для осей Y и Z.

; ; .

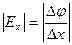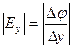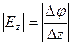В цилиндрической системе координат выражение градиента потенциала будет иметь следующий вид:

.

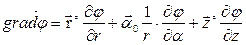А в сферической системе координат:

.

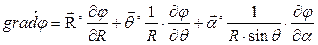Дифференциальный оператор Гамильтона (оператор Набла)

Для сокращения записи операций над скалярными и векторными величинами употребляют дифференциальный оператор Гамильтона или оператор Набла:

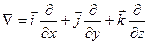
Под дифференциальным оператором Гамильтона понимают сумму частных производных по 3-м координатным осям, умноженных на соответствующие единичные векторы (орты).

Применим оператор Гамильтона к потенциалу:

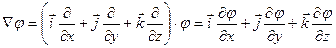
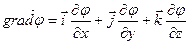
Правые части одинаковы, значит, будут одинаковы и левые части:

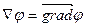
Оператор Гамильтона сочетает в себе как векторные, так и скалярные свойства и может быть применен к скалярным и векторным функциям.

Дата добавления: 2015-07-30 ; просмотров: 11001 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Электрическое поле характеризуется тем, что работа перемещения заряда в поле не зависит от пути перехода из начального положения и является функцией только начального и конечного положений. Работа перемещения заряда по замкнутому контуру в электростатическом поле равна нулю. Из этих фактов следует, что электростатическое поле носит потенциальный характер и характеризуется особой величиной –
потенциалом . Величина

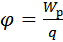, (12)

Где W_р – потенциальная энергия заряда q, называется потенциалом поля в данной точке и используется наряду с напряженностью поля 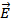для описания электрических полей.

Как следует из приведенной формулы, потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.

В то время, как напряженности поля складываются при наложении полей векторно, потенциалы складываются алгебраически. По этой причине вычисление потенциалов проще, чем вычисление напряженностей поля.

Из (12) вытекает, что заряд q, находящийся в точке поля с потенциалом , обладает потенциальной энергией

.

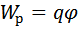Следовательно, работа сил над зарядом q может быть выражено через разность потенциалов

.

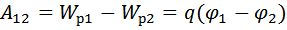Таким образом, работа, совершаемая над зарядом силами поля, равна произведению величины заряда на разность потенциалов в начальной и конечной точках.

Если заряд q из точки с потенциалом удаляется на бес­конечность, где по условию потенциал равен нулю, то работа сил поля равна

.

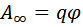Отсюда следует, что потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при уда­лении его из денной точки на бесконечность.

Последнее соотношение модно использовать для установления еди­ниц измерения потенциала. За единицу потенциала следует принять потенциал в такой точке поля, для перемещения в которую из беско­нечности единичного положительного заряда необходимо совершить работу, равную единице. Так, за СИ – единицу потенциала, называе­мую вольтом (В), принимается потенциал в такой точке, для переме­щения в которую из бесконечности заряда, равного 1 кулону, нужно совершить работу в 1Дж: 1Дж= 1Кл*1В.

Отсюда 1В =1Дж/1Кл.

Эквипотенциальные поверхности.

Для наглядного изображения поля можно вместо линий напряженнос­тей воспользоваться поверхностями равного потенциала или эквипо­тенциальными поверхностями.

Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью.

Если потенциал задан как функция X, Y, Z, то уравнение эквипотенциальной поверхности имеет вид:

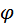(x,y,z) = const.

Эти поверхности проводятся в пространстве таким образом, чтобы численное значение потенциала на двух соседних поверхностях от­личалось повсюду на одинаковую величину ∆ (например на I В).

В качестве примера рассмотрим эквипотенциальные поверхности поля точечного заряда 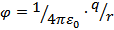. Отсюда следует, что 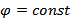при r = const т.е. поверхности равного потенциала будут концентрическими сферами, описанными вокруг источника поля на возрастающих расстояниях друг от друга, как это показано на рис.4.

Проведем на рис.4 линии напряженности поля. Эти линии выходят из точечного заряда и направ­лены вдоль радиусов, т.е. перпендикулярны к эквипотенциальным поверхностям.

Эта взаимная перпендикулярность линий поля и эквипотенциальных поверхностей остается справедливой и для сколь угодно сложных электро­статических полей.

Градиент потенциала. Связь между напряжен­ностью и потенциалом.

Электрическое поле можно описать либо с помощью векторной величины 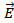, либо с помощью скалярной величины . Очевидно, что между этими величинами должна существовать определенная связь. Если учесть, что 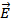пропорционально силе, действующей на заряд, а – потенциальной энергии заряда, легко сообра­зить, что эта связь должна быть аналогична связи между потенци­альной энергией и силой. .

Работа сил поля над зарядом q на отрезке пути dl мо­жет быть представлена с одной стороны, как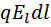

где – проекция вектора напряженности на направление элемен­тарного перемещения с другой стороны, как убыль потенциальной энергии заряда, т.е. – 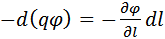. Приравнивая эти выражения, получим: 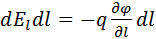, откуда находим, что 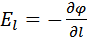, где через l обозначено произвольно выбранное направление в пространстве.

В частности, в декартовой системе координат:

; ; ;

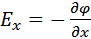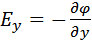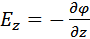откуда .

Выражение в скобках называется градиентом скаляра .

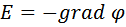. (13)

Таким образом, напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком.

Градиент некоторой скалярной величины 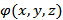есть век­торная величина со следующими свойствами. Направление градиента совладеет с направлением, в котором при смещении из данной точ­ки функция возрастает с наибольшей скоростью. Величина 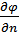по этому направлению дает модуль градиента. Частные про­изводные 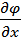, , 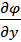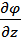представляют собой проекции гра­диента на оси x,y,z .

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9402 – | 7312 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно