В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами- изготовителями. На складе имеются электродвигатели этих заводов соответственно в количестве  ,
, 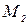 , и
, и 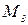 штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно
штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно  . Рабочий берет случайно один электродвигатель и монтирует его к устройству. Найти вероятность того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом.
. Рабочий берет случайно один электродвигатель и монтирует его к устройству. Найти вероятность того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом.
Значения параметров вычислить по следующим формулам
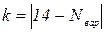 ,
, 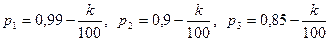
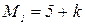 ,
, 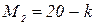 ,
, 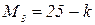 .
.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8810 –  | 7168 –
| 7168 –  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Пример №1 . Прибор может собираться из высококачественных деталей и из деталей обычного качества. Около 40% приборов собираются из высококачественных деталей. Если прибор собран из высококачественных деталей, его надежность (вероятность безотказной работы) за время t равна 0,95; если из деталей обычного качества — его надежность равна 0,7. Прибор испытывался в течение времени t и работал безотказно. Найдите вероятность того, что он собран из высококачественных деталей.
Решение. Возможны две гипотезы: H1 — прибор собран из высококачественных деталей; H2 — прибор собран из деталей обычного качества. Вероятности этих гипотез до опыта: P(H1) = 0,4, P(H2) = 0,6. В результате опыта наблюдалось событие A — прибор безотказно работал время t. Условные вероятности этого события при гипотезах H1 и H2 равны: P(A|H1) = 0,95; P(A|H2) = 0,7. По формуле (12) находим вероятность гипотезы H1 после опыта:
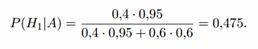
Пример №2 . Два стрелка независимо один от другого стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго 0,4. После стрельбы в мишени обнаружена одна пробоина. Предполагая, что два стрелка не могут попасть в одну и ту же точку, найдите вероятность того, что в мишень попал первый стрелок.
Решение. Пусть событие A — после стрельбы в мишени обнаружена одна пробоина. До начала стрельбы возможны гипотезы:
H1 — ни первый, ни второй стрелок не попадет, вероятность этой гипотезы: P(H1) = 0,2 · 0,6 = 0,12.
H2 — оба стрелка попадут, P(H2) = 0,8 · 0,4 = 0,32.
H3 — первый стрелок попадет, а второй не попадет, P(H3) = 0,8 · 0,6 = 0,48.
H4 — первый стрелок не попадет, а второй попадет, P (H4) = 0,2 · 0,4 = 0,08.
Условные вероятности события A при этих гипотезах равны:
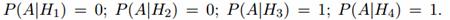
После опыта гипотезы H1 и H2 становятся невозможными, а вероятности гипотез H3 и H4
будут равны:

Пример №3 . В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями. На складе имеются электродвигатели названных заводов соответственно в количестве 19,6 и 11 шт., которые могут безотказно работать до конца гарантийного срока соответственно с вероятностями 0,85, 0,76 и 0,71. Рабочий берет случайно один двигатель и монтирует его к устройству. Найдите вероятность того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом-изготовителем.
Решение. Первым испытанием является выбор электродвигателя, вторым — работа электродвигателя во время гарантийного срока. Рассмотрим следующие события:
A — электродвигатель работает безотказно до конца гарантийного срока;
H1 — монтер возьмет двигатель из продукции первого завода;
H2 — монтер возьмет двигатель из продукции второго завода;
H3 — монтер возьмет двигатель из продукции третьего завода.
Вероятность события A вычисляем по формуле полной вероятности:

Условные вероятности заданы в условии задачи:

Найдем вероятности 



Пример №4 . Вероятности того, что во время работы системы, которая состоит из трех элементов, откажут элементы с номерами 1, 2 и 3, относятся как 3: 2: 5. Вероятности выявления отказов этих элементов равны соответственно 0,95; 0,9 и 0,6.
а) Найдите вероятность обнаружения отказа в работе системы.
б) В условиях данной задачи во время работы системы обнаружен отказ. Какой из элементов вероятнее всего отказал?
Решение.
Пусть А – событие отказа. Введем систему гипотез H1 – отказ первого элемента, H2 – отказ второго элемента, H3 – отказ третьего элемента.
Находим вероятности гипотез:
P(H1) = 3/(3+2+5) = 0.3
P(H2) = 2/(3+2+5) = 0.2
P(H3) = 5/(3+2+5) = 0.5
Согласно условию задачи условные вероятности события А равны:
P(A|H1) = 0.95, P(A|H2) = 0.9, P(A|H3) = 0.6
а) Найдите вероятность обнаружения отказа в работе системы.
P(A) = P(H1)*P(A|H1) + P(H2)*P(A|H2) + P(H3)*P(A|H3) = 0.3*0.95 + 0.2*0.9 + 0.5*0.6 = 0.765
б) В условиях данной задачи во время работы системы обнаружен отказ. Какой из элементов вероятнее всего отказал?
P1 = P(H1)*P(A|H1)/ P(A) = 0.3*0.95 / 0.765 = 0.373
P2 = P(H2)*P(A|H2)/ P(A) = 0.2*0.9 / 0.765 = 0.235
P3 = P(H3)*P(A|H3)/ P(A) = 0.5*0.6 / 0.765 = 0.392
Максимальная вероятность у третьего элемента.
Пусть событие А может наступить лишь при появлении одного из несовместных событий (гипотез) Н1, Н2…Нn, образующих полную группу ( 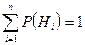 ). Тогда вероятность события А равна сумме произведений вероятностей каждой из гипотез на собственную условную вероятность события А:
). Тогда вероятность события А равна сумме произведений вероятностей каждой из гипотез на собственную условную вероятность события А:
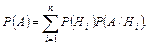
Это равенство называют формулой полной вероятности.
Если известно, что событие А произошло, то вероятности гипотез могут быть найдены по формулам Бейеса:
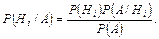
Пример 35. В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями в количестве 19, 6, 11 штук и могут безотказно работать до конца гарантийного срока соответственно с вероятностями 0.85, 0.76 и 0.71. Рабочий берет случайно один двигатель и монтирует его к устройству.
1) Найти вероятность того, что этот электродвигатель проработает до конца гарантийного срока.
2) Двигатель не вышел из строя. Найти вероятность того, что он изготовлен соответственно первым или вторым заводом.
Решение. Рассмотрим следующие события:
А – двигатель работает безотказно до конца гарантийного срока.
Гипотеза Hi – рабочий возьмет двигатель из продукции “i”-го завода. Из условия задачи P(H1)=19/36, т.к. всего двигателей 36, а первый завод поставил 19; P(H2)=6/36; P(H3)=11/36. 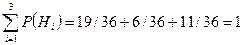 , следовательно гипотезы H1, H2, H3 образуют полную группу. Условная вероятность того, что двигатель не выйдет из строя, если он изготовлен первым заводом P(A/H1)=0.85; для второго завода P(A/H2)=0.76; для третьего – P(A/H3)=0.71. Тогда:
, следовательно гипотезы H1, H2, H3 образуют полную группу. Условная вероятность того, что двигатель не выйдет из строя, если он изготовлен первым заводом P(A/H1)=0.85; для второго завода P(A/H2)=0.76; для третьего – P(A/H3)=0.71. Тогда:
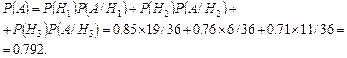
По формуле Бейеса найдем условные вероятности гипотез:
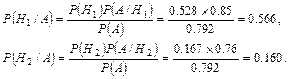
36. В вычислительной лаборатории имеются шесть клавишных автоматов и четыре полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 0,95; для полуавтомата эта вероятность равна 0,8. Студент производит расчет на наудачу выбранной машине. Найти вероятность того, что до окончания расчета машина не выйдет из строя.
37. В ящике содержится 12 деталей, изготовленных на заводе №1, 20 деталей – на заводе №2 и 18 деталей – на заводе №3. Вероятность того, что деталь, изготовленная на заводе № 1, отличного качества, равна 0,9; для деталей, изготовленных на заводах № 2 и № 3, эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества.
38. В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.
39. Вероятности того, что во время работы цифровой электронной машины произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах, относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.
36. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
40. Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6, 0,5 и 0,4.
41. Партия транзисторов, среди которых 10% дефектных, поступила на проверку. Схема проверки такова, что с вероятностью 0.95 дефект (если он есть) обнаруживается и существует ненулевая вероятность 0.03 того, что исправный транзистор будет признан дефектным. Какова вероятность того, что случайно выбранный транзистор будет дефектным?
42. На вход радиолокационного устройства с вероятностью 0.8 поступает смесь полезного сигнала с помехой, а с вероятностью 0.2 – только помеха. Если поступает полезный сигнал с помехой, то устройство регистрирует наличие какого-то сигнала с вероятностью 0.7; если только помеха – то с вероятностью 0.3. Известно, что устройство зарегистрировало наличие какого-то сигнала. Найти вероятность того, что в его составе есть полезный сигнал.
43. В коробке с немаркированными цифровыми микросхемами лежит 200 шестиэлементных инверторов, 100 схем совпадения, 50 JK-триггеров, 25 декадных счетчиков и 25 четырехразрядных сдвиговых регистров.
а) Какова вероятность того, что взятая наугад микросхема окажется JK-триггером?
б) Какова вероятность того, что взятая наугад микросхема не является инвертором?
в) Если известно, что первая взятая микросхема оказалась сдвиговым регистром, то какова вероятность вытаскивания такой же микросхемы во второй раз?
44. Для задачи 44 дополнительно известно, что неисправны 10 % инверторов, 15 % схем совпадения, 18 % триггеров, а также 20 % счетчиков и сдвиговых регистров.
а) Какова вероятность вытаскивания наугад исправного счетчика?
б) Какова вероятность того, что извлеченная наугад микросхема исправна, если известно, что это JK-триггер?
в) Какова вероятность того, что извлеченная микросхема — декадный счетчик, . если известно, что она исправна?
45. Предприятие выпускает небольшие электрические двигатели мощностью 73,6, 368 и 736 Вт, работающие либо от однофазной сети питания переменного тока с номинальным напряжением 120 или 240 В, либо от трехфазной сети с номинальным напряжением 240 В. Различать эти двигатели можно только по маркировке. На складе имеется 3000 таких двигателей в количествах, указанных в таблице. На одном из двигателей маркировка отсутствует. Определите вероятность того, что
| Мощность двигателя, Вт | Количество двигателей с питанием от сети переменного тока с напряжением | |
| 120 В | 240 В (однофазная сеть) | 240 В (трехфазная сеть) |
| 73,6 |
а) мощность этого двигателя равна 368 Вт,
б) сеть его питания должна быть однофазной с напряжением 240 В,
в) мощность двигателя 736 Вт, и он работает от трехфазной сети 240 В,
г) мощность двигателя 73,6 Вт и он предназначен для работы при напряжении сети 120 В.
47. Пусть для случая, описанного в предыдущей задаче, 10% двигателей для сети питания с напряжением 120 В и 5 % двигателей для однофазной сети питания с напряжением 240 В промаркированы неправильно. Какова вероятность того, что произвольно взятый двигатель
а) окажется неправильно промаркирован?
б) из группы двигателей для однофазной сети 240 В неправильно промаркирован?
