Содержание
Система состоит из двух концентрических проводящих сфер, причем на внутренней сфере радиусом R1 находится заряд q1. Какой заряд q2 следует поместить на внешнюю сферу радиусом R2, чтобы потенциал внутренней сферы стал равным нулю? Как будет зависеть при этом потенциал j от расстояния r до центра системы?
Запишем выражения для потенциала вне системы (jII) и в области между сферами (jI):
, 
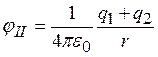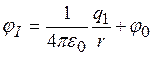, где j0 – некоторая постоянная. Ее значение легко найти из граничного условия: при r = R2 потенциал jII = jI. Отсюда
.
.
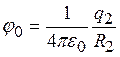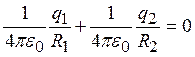
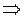
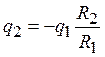Зависимость j (r) будет иметь вид:
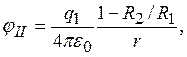
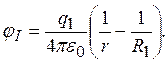
Урок №3
Электрическое поле в диэлектрике. Энергия электрического поля
Поле в диэлектрике является суперпозицией поля E0 сторонних зарядов (q) и поля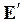 
связанных (поляризованных) зарядов (q’):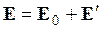 
Поляризованностью диэлектрика называется суммарный дипольный момент единицы объема:
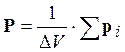
Для большинства диэлектриков, P= æ . e0 . E, æ – диэлектрическая восприимчивость.
Поток вектора P через замкнутую поверхность, равен связанному заряду, находящемуся в объеме, ограниченном этой поверхностью, взятому с обратным знаком:
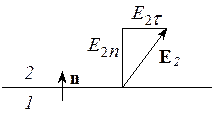
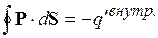
На границе раздела двух диэлектриков:
,
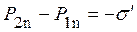s¢ – поверхностная плотность связанных зарядов.
В диэлектрике теорема Гаусса для вектора E будет такой:
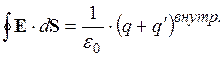, т.е. следует учитывать все заряды – и сторонние, и связанные, охватываемые поверхностью S. Это неудобно, поэтому вводят вспомогательный вектор:
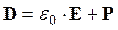
Как нетрудно убедиться, поток вектора D через замкнутую поверхность определяется только сторонними зарядами:
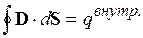
Для изотропных диэлектриков:
где e – диэлектрическая проницаемость вещества.
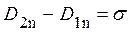, где s – поверхностная плотность сторонних зарядов
Энергия взаимодействия системы точечных зарядов: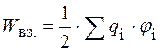 
, где ji – потенциал поля, создаваемого всеми остальными зарядами (кроме qi) в точке, где расположен заряд qi.
Если рассмотреть уединенный проводник, то энергия взаимодействия зарядов проводника между собой даст нам собственную энергию проводника:
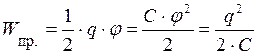, где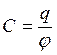 
– емкость проводника
При подсчете полной энергии системы следует учитывать собственную энергию всех зарядов и энергию их взаимодействия.
Оказывается, что энергию системы зарядов можно выразить через напряженность электрического поля, создаваемого этими зарядами. Объемную плотность электрической энергии можно найти по формуле:
.
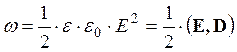Энергию электрического поля в некотором объеме V можно найти так:
.
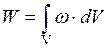Если интеграл взять по всему объему, где существует электрическое поле системы зарядов, то получим полную энергию этой системы.
Рассмотрим систему двух заряженных тел в вакууме (e= 1). Результирующее поле: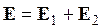 
.
Полная энергия этой системы найдется:
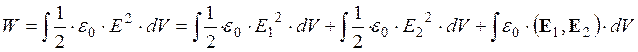, где интегрирование ведется по всему пространству.
Понятно, что первое и второе слагаемые дают собственную энергию первого и второго проводников соответственно, а третье – энергию их взаимодействия.
Работа сил электростатического поля, как поля потенциальных сил, может быть найдена как убыль энергии: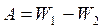 
.
Энергия заряженного конденсатора: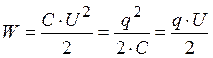 
.
В плоском конденсаторе однородное электрическое поле локализовано только между его обкладками, поэтому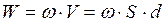 
.
Примеры решения задач
Задача №1
Первоначально пространство между обкладками плоского конденсатора заполнено воздухом, и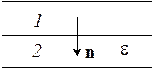 
напряженность поля в зазоре равна Е0. Затем половину зазора, как показано на рисунке, заполнили однородным изотропным диэлектриком с проницаемостью e. Найти модули векторов E и D в обеих частях зазора, если при введении диэлектрика напряжение между обкладками не менялось.
До введения диэлектрика напряжение между обкладками:
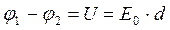, т.к. поле однородное, d – расстояние между обкладками.
Магазин готовых контрольных – дипломных работ запись закреплена
Политехнический институт (ПИ) СФУ Контрольная Дисциплина: физика. Контрольные №3 и №4. Вариант 0.
Контрольная работа №3
310. Маленький шарик, несущий заряд 317 нКл, находится на рас-стоянии 2 см от плоской металлической стенки, соединенной с Землей. С какой силой они взаимодействуют?
320. Электрическое поле создано двумя бесконечными параллель-ными равномерно заряженными пластинами с поверхностными плотно-стями заряда плюс 41 нКл/м2 и минус 84 нКл/м2. Определить напряжен-ность поля между пластинами.
330. Какой энергией обладает заряженный до разности потенциалов 861 В конденсатор с площадью пластин 6193 см2, если расстояние между пластинами конденсатора, заполненного диэлектриком с диэлектрической проницаемостью 40, равно 737 мкм.
344. До одного и того же потенциала 54 В заряжены 5313 одинако-вых шарообразных капелек ртути. Каков будет потенциал большой капли, получившейся в результате слияния этих капелек?
350. Плоский воздушный конденсатор, пластины которого располо-жены горизонтально, наполовину залит диэлектрической жидкостью с от-носительной проницаемостью 26. Какую часть конденсатора надо залить этой же жидкостью при вертикальном расположении пластин, чтобы емко-сти в обоих случаях были одинаковы?
354. В некоторой точке изотропного диэлектрика с относительной диэлектрической проницаемостью 43 электрическое смещение имеет зна-чение 523 нКл/м2. Чему равна поляризованность в этой точке диэлектрика в нанокулонах на метр квадратный?
370. По проводнику длиной 2,4 м и площадью поперечного сечения 0,001 м2 протекает ток силой 0,05 А. Определите удельную электропро-водность материала проводника, если к его концам приложена разность потенциалов 20 В. Ответ дать в единицах СИ.
380. ЭДС батареи равна 12 В, сила тока короткого замыкания 5 А. Какую наибольшую мощность может дать батарея во внешней цепи? Ответ дать в единицах СИ.
Контрольная работа №4
410. По двум бесконечно длинным параллельным проводникам, расположенным на расстоянии 61 см друг от друга, текут противополож-но направленные одинаковые токи 62 А. Найти напряженность магнитного поля в точке, расположенной от каждого проводника на таком же расстоя-нии, что и расстояние между проводниками.
417. По кольцу радиусом 99 см течет ток 4 А. Плоскость кольца по диаметру изогнута под прямым углом. Определить величину магнитной индукции в центре кольца.
430. Плоский квадратный контур со стороной 7 см свободно устано-вился в однородном магнитном поле, индукция которого равна 0,4 Тл. При повороте контура внешними силами вокруг оси, проходящей через середины противоположных сторон, на угол 60° была совершена работа 188 мДж. Определить силу тока, текущего в контуре. Ток при повороте не изменяется.
440. Протон, прошедший разность потенциалов 1731 В, влетел в од-нородное магнитное поле с напряженностью 423 кА/м и начал двигаться по окружности. Вычислить ее радиус.
450. Короткая катушка, имеющая 321 виток, вращается с угловой скоростью 6 рад/с в однородном магнитном поле вокруг оси, совпадающей с ее диаметром и перпендикулярной линиям поля. Найти значение ЭДС индукции для момента времени, когда плоскость по-перечного сечения катушки составляет угол 60° с линиями по-ля.
460. Соленоид содержит 2468 витков, а сила тока в его обмотке рав-на 2 А. Найти энергию магнитного поля внутри соленоида, полагая его бесконечно длинным. Магнитный поток через поперечное сечение солено-ида равен 314 мкВб.
470. Емкость и индуктивность колебательного контура равны и Через сколько времени после начала зарядки конденсатора его энергия в 31 раз превысит энергию катушки индуктивно-сти? Сопротивлением контура пренебречь.
480. Какую индуктивность надо включить в колебательный контур, чтобы при емкости 2 мкФ получить звуковую частоту 1000 Гц? Сопротив-лением контура пренебречь.
Электрическое поле в диэлектрической среде создается как свободными, так и связанными зарядами, так что вектор напряженности E, характеризующий результирующее поле в диэлектрике,
.
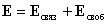Если обозначить объемную плотность свободных зарядов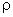 
, а связанных зарядов 
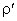, то присутствие связанных зарядов отразится в теореме Гаусса следующим образом:
,
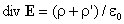в дифференциальной форме, либо в интегральной форме
.
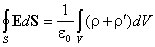С учетом выражения (2.1)
,
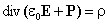откуда для вектора электрического смещения (индукции) находим
.
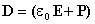Последнее выражение показывает, что вектор электрической индукции учитывает поляризованность среды. Возвращаясь к соответствующим формулировкам теоремы Гаусса
; 
,
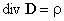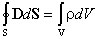можно видеть, что вектор электрического смещения характеризует источники электрического поля, т. е. свободные заряды, на которых этот вектор начинается и заканчивается. Так как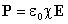 
, то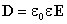 
.
Напряженность электрического поля характеризует как свободные, так и связанные заряды, поэтому вектор напряженности терпит разрывы на границах областей, где присутствуют связанные заряды, например на границе раздела двух диэлектриков с различными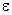 
.
1) Как определяется вектор электрического смещения. Каково его направление
2) В некоторой точке изотропного диэлектрика с проницаемостью смещение имеет значение D. Чему равна поляризованность P в этой точке
3) Чему равен поток вектора электрического смещения через замкнутую поверхность в электрическом поле