Вектор электрической индукции формула

Рассмотрим, как меняется значение вектора Е на границе раздела двух сред, например, воздуха (ε 1) и воды (ε = 81). На­пряженность поля в воде уменьшается скачком в 81 раз. Такое по­ведение вектора Е создает определенные неудобства при расчете полей в различных средах. Чтобы избежать этого неудобства вводят новый вектор D – вектор индукции или электрического смещения поля. Связь векторов D и Е имеет вид

Очевидно, для поля точечного заряда электрическое смещение будет равно

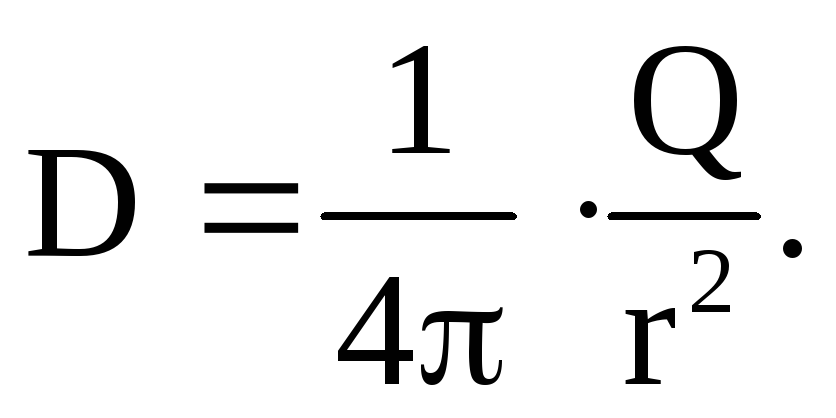
Нетрудно увидеть, что электрическое смещение измеряется в Кл/м 2 , не зависит от свойств и графически изображается линиями, анало­гичными линиям напряженности.

Направление силовых линий поля характеризует направле­ние поля в пространстве (силовые линии, конечно, не существуют, их вводят для удобства иллюстрации) или направление вектора на­пряженности поля. С помощью линий напряженности можно характеризовать не только направление, но и величину напряженно­сти поля. Для этого условились прово­дить их с определенной густотой, так, чтобы число линий напряженности, про­низывающих единицу поверхности, пер­пендикулярной линиям напряженности, было пропорционально модулю вектора Е (рис. 78). Тогда число линий, пронизываю­щих элементарную площадку dS, нормаль к которой n образует угол α с вектором Е, равно E dScos α = E_n dS,

где E_n – составляющая вектора Е по направлению нормали n. Величину dФ_Е= E_ndS = EdS называют потоком вектора напряженности че­рез площадку dS (dS = dS·n).

Для произвольной замкнутой поверхности S поток вектора Е через эту поверхность равен

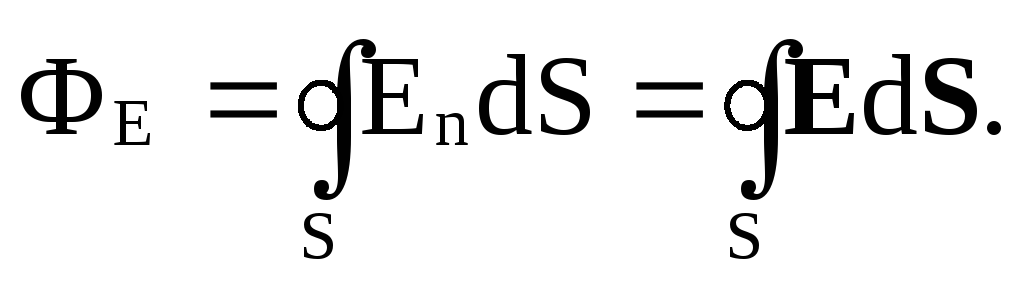
Аналогичное выражение имеет поток вектора электрического сме­щения Ф_D

.

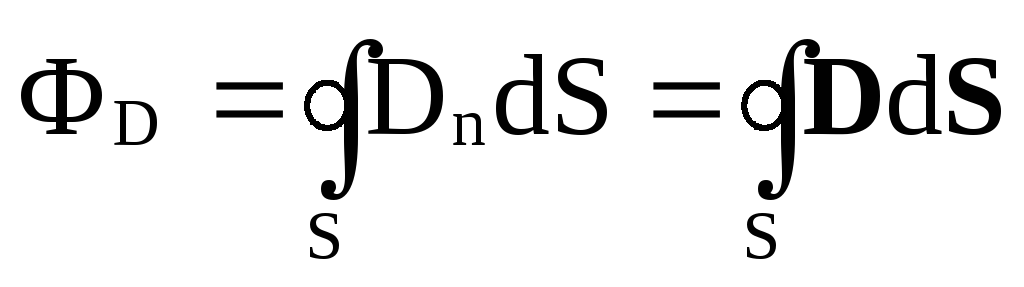Теорема Остроградского-Гаусса

Эта теорема позволяет определить поток векторов Е и D от любого количества зарядов. Возьмем точечный заряд Q и определим поток вектора Е че­рез шаровую поверхность радиуса r , в центре которой он располо­жен.

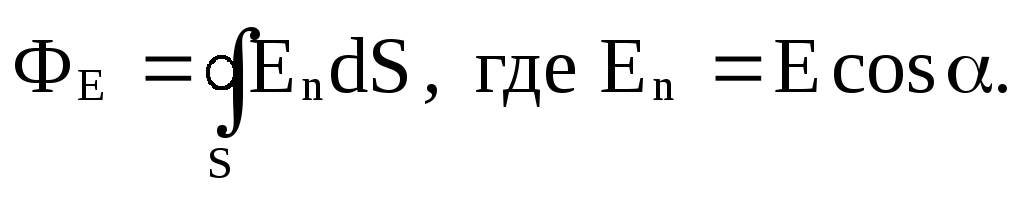
Для шаровой поверхности α = 0, cos α = 1, E_n = E, S = 4 πr 2 и

Подставляя выражение для Е получим

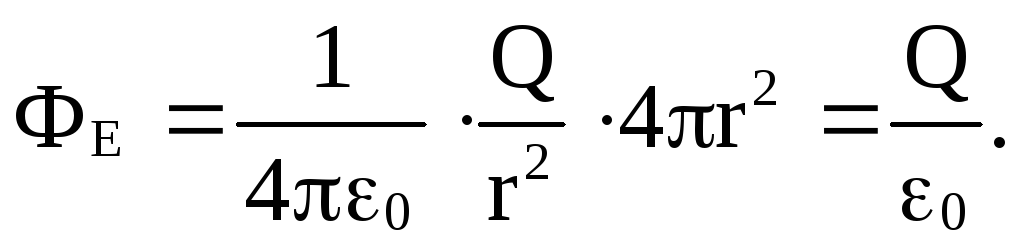
Таким образом, из каждого точечного заряда выходит поток Ф_Е вектора Е равный Q/ ε₀ . Обобщая этот вывод на общий случай про­извольного числа точечных зарядов дают формулировку теоремы: полный поток вектора Е через замкнутую поверхность про­извольной формы численно равен алгебраической сумме электрических зарядов, заключенных внутри этой поверхно­сти, поделенной на ε₀ , т.е.

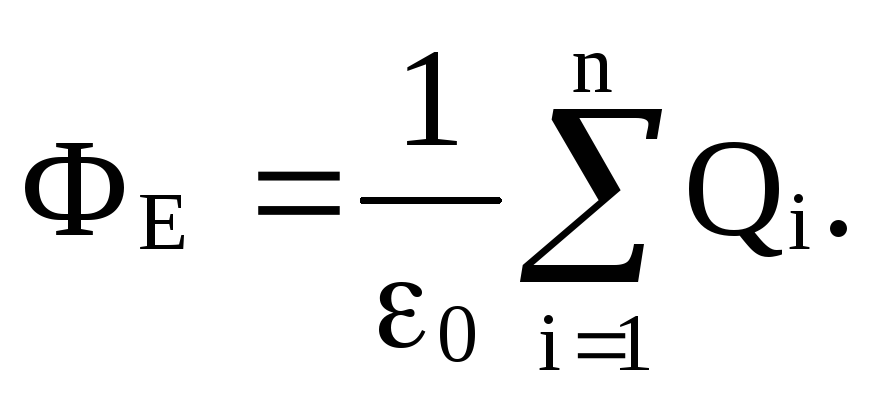
Для потока вектора электрического смещения D можно получить аналогичную формулу

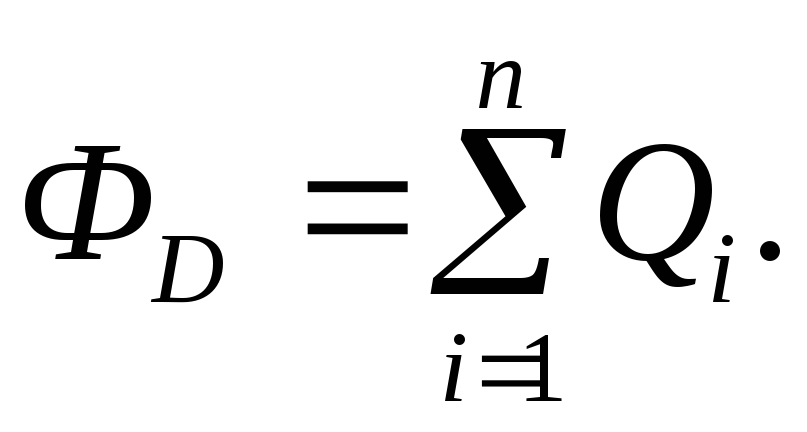
поток вектора индукции через замкнутую поверхность равен алгебраической сумме электрических зарядов, охватываемых этой поверхностью.

Если взять замкнутую поверхность, не охватывающую заряд, то каждая линия Е и D будут пересекать эту поверхность дважды – на входе и выходе, поэтому суммарный поток оказывается равным нулю. Здесь необходимо учитывать алгебраическую сумму линий, входящих и выходящих.

Применение теоремы Остроградского-Гаусса для расчета элек­трических полей, создаваемых плоскостями, сферой и цилин­дром

Сферическая поверхность радиуса R несет на себе заряд Q, равномерно распределенный по поверхности с поверхностной плотностью σ

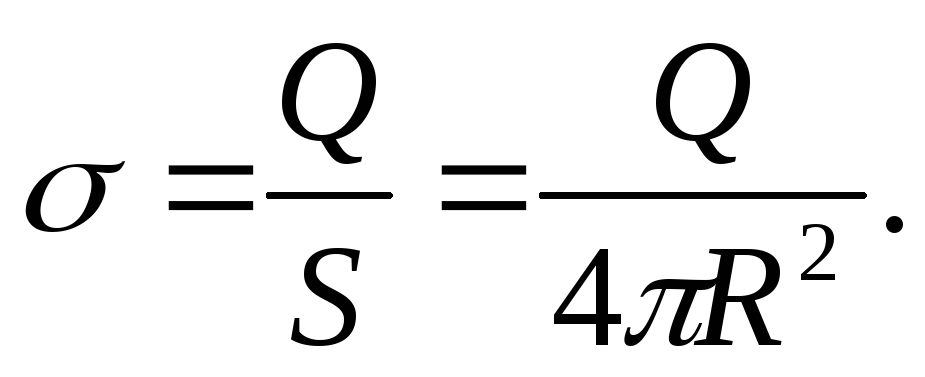
Возьмем точку А вне сферы на расстоянии r от центра и проведем мысленно сферу радиуса r симметричную заряженной (рис. 79). Ее площадь S = 4 πr 2 . Поток вектора Е будет равен

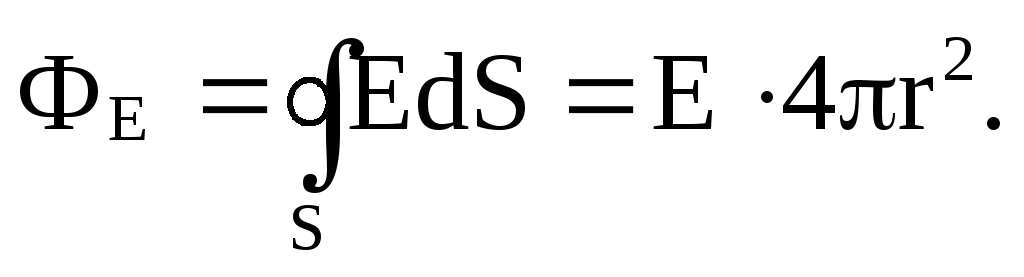
По теореме Остроградского-Гаусса 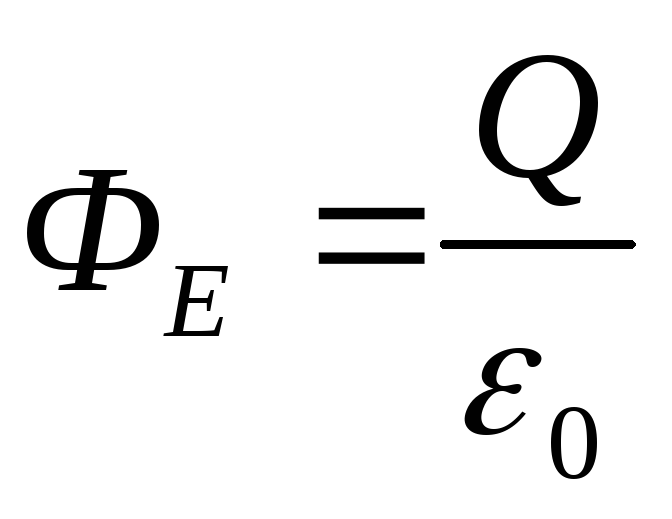, следовательно,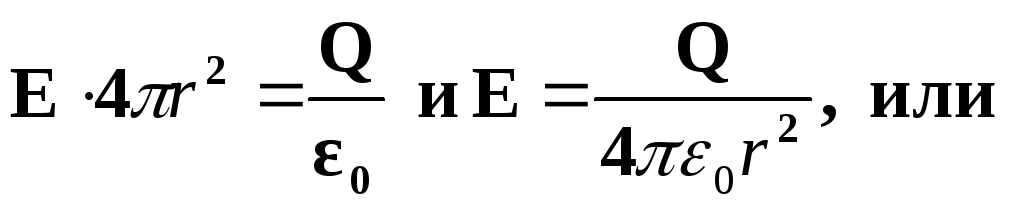учитывая, чтоQ = σ·4 πr 2 , получим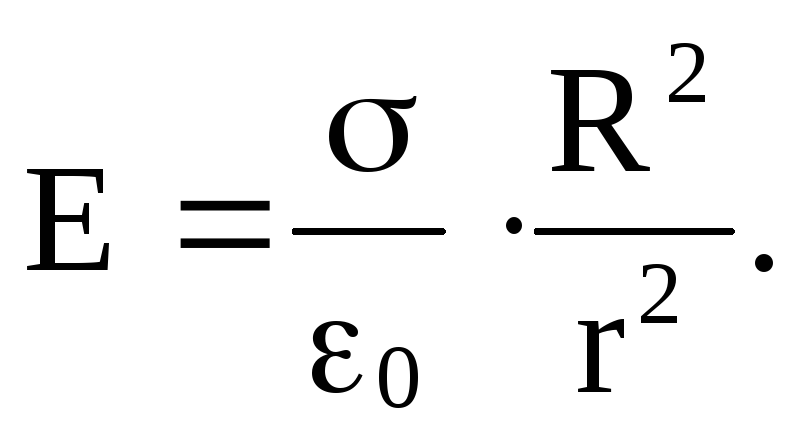

Для точек, находящихся на поверхности сферы (R = r )

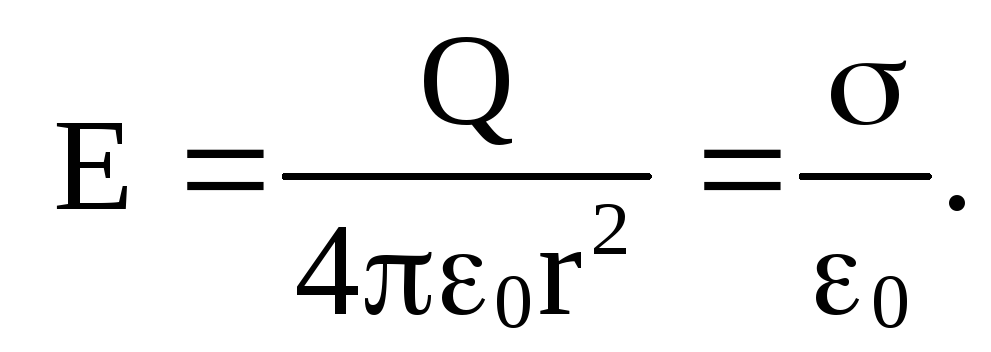
Для точек, находящихся внутри полой сферы (внутри сферы нет за­ряда), Е = 0.

2. Полая цилиндрическая поверхность радиусом R и длиной l заряжена с постоянной поверхностной плотностью заряда (Рис. 80). Проведем коаксиальную цилиндрическую поверхность радиусаr > R.

Поток вектора Е через эту поверхность

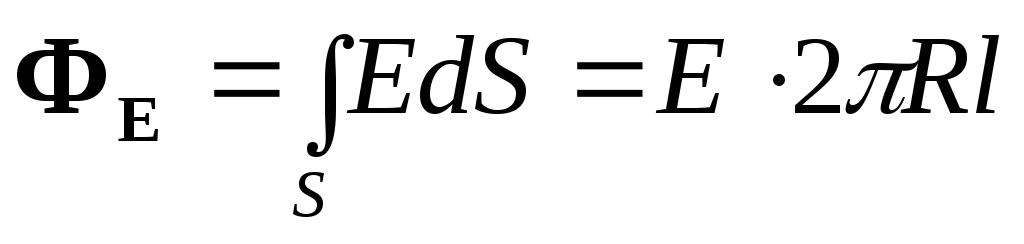
По теореме Гаусса

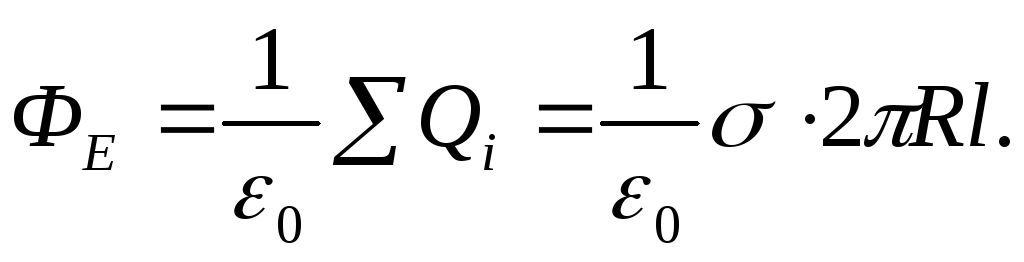
Приравнивая правые части приведенных равенств, получим

.

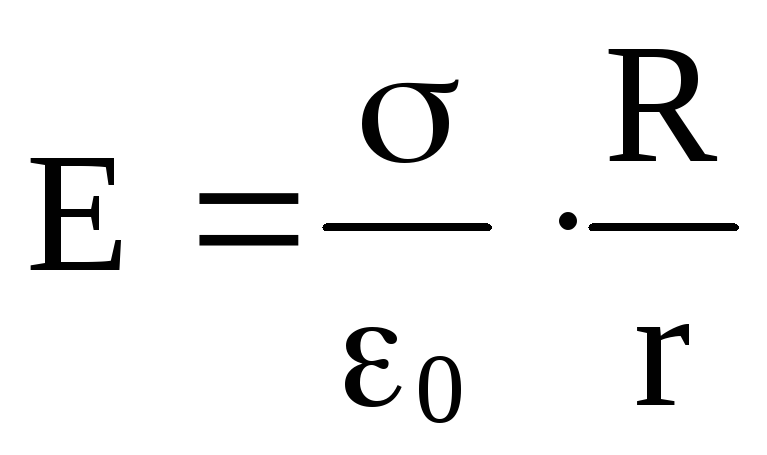Если задана линейная плотность заряда цилиндра (или тонкой нити) 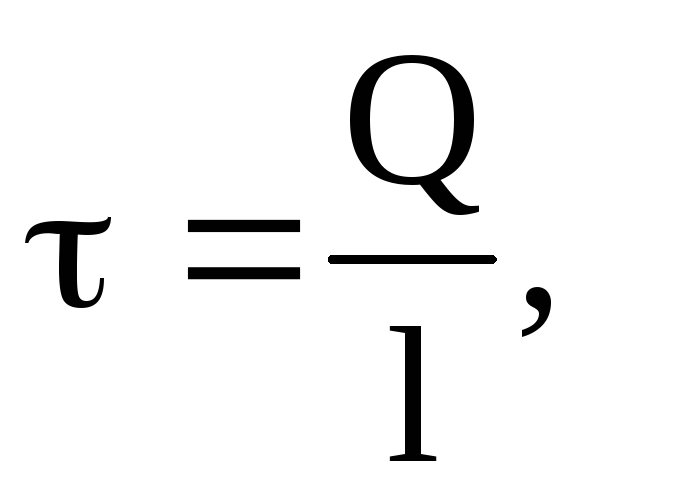то

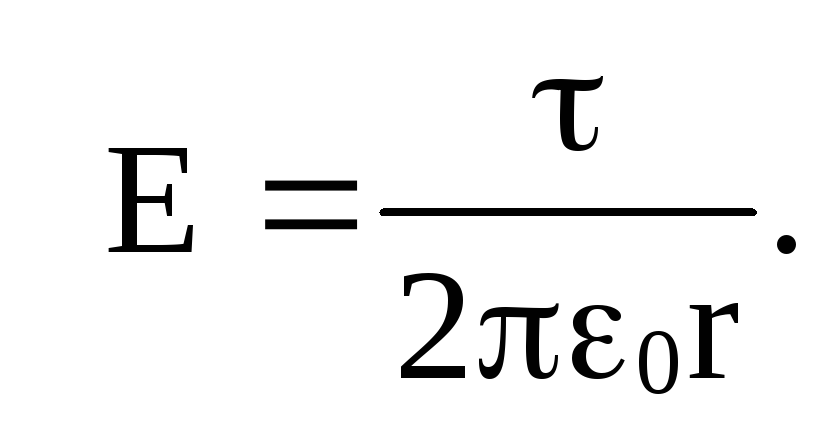
3. Поле бесконечных плоскостей с поверхностной плотно­стью заряда σ (рис. 81).

Рассмотрим поле, создаваемое бесконечной плоскостью. Из сооб­ражений симметрии вытекает, что напряженность в любой точке поля имеет направление, перпендикулярное к плоскости.

В симметричных точках Е будет одинакова по величине и противоположна по направлению.

Построим мысленно поверхность цилиндра с основанием ΔS. Тогда через каждое из оснований цилиндра будет выходить поток

Ф_Е = Е ΔS, а суммарный поток через цилиндрическую поверхность будет равен Ф_Е = 2Е ΔS.

Внутри поверхности заключен заряд Q = σ · ΔS. Согласно теореме Гаусса должно выполняться

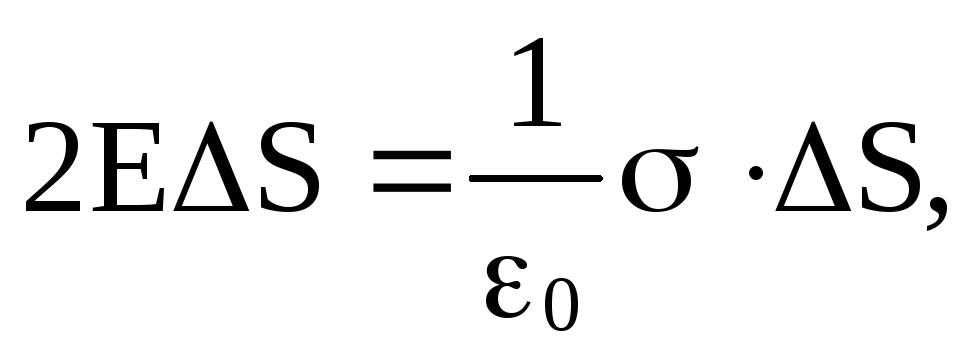откуда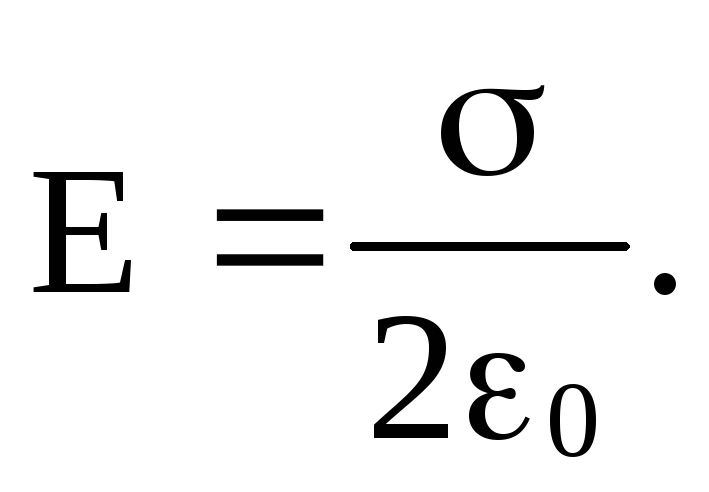

Полученный результат не зависит от высоты выбранного цилиндра. Таким образом напряжённость поля Е на любых расстояниях одинакова по величине.

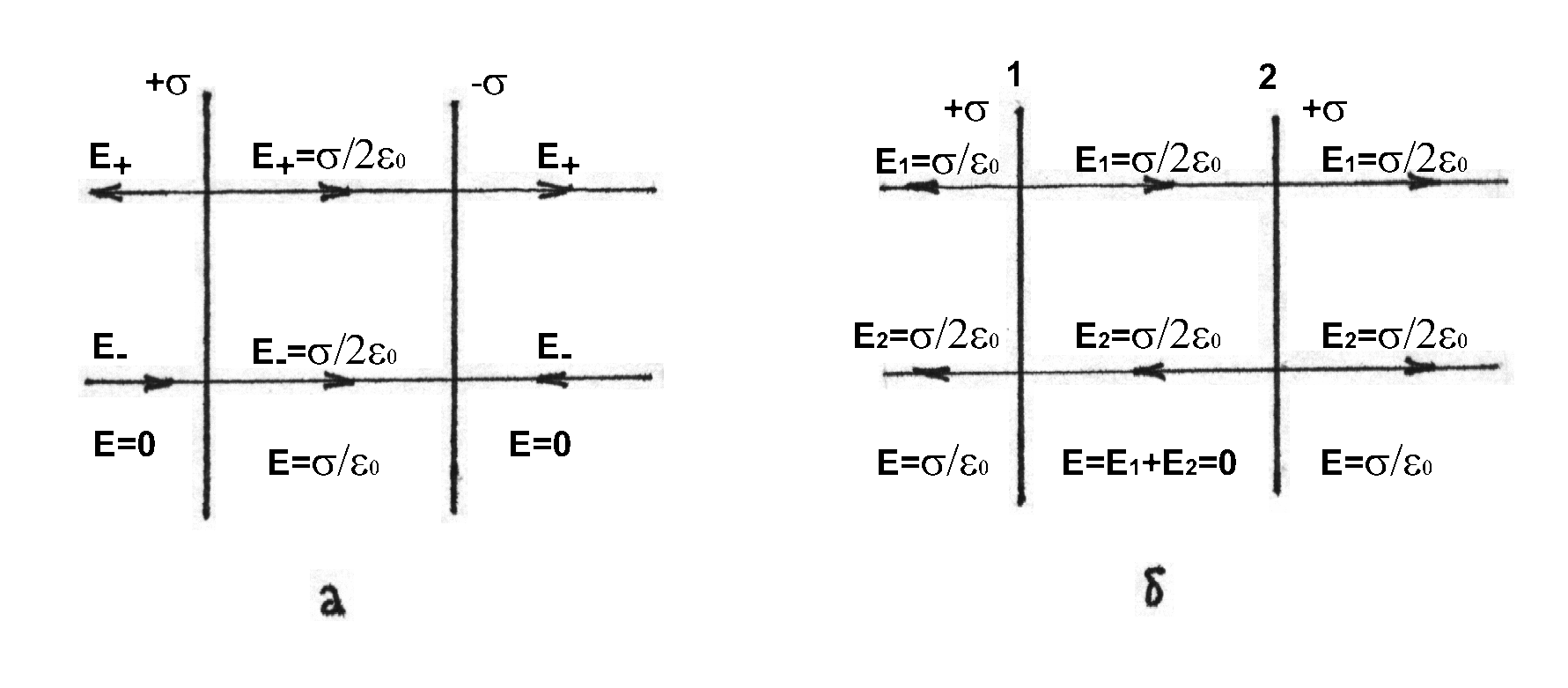
Для двух разноименно заряженных плоскостей с одинаковой по­верхностной плотностью заряда σ по принципу суперпозиции вне про­странства между плоскостями напряжённость поля равна нулю Е = 0, а в пространстве между плос­костями 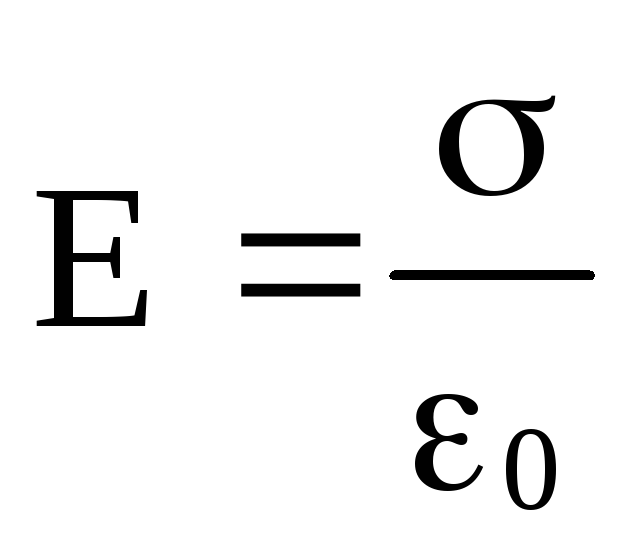(рис. 82а). В случае, если плоскости заряжены одноименными зарядами с одинаковой поверхностной плотностью зарядов, наблюдается об­ратная картина (рис. 82б). В пространстве между плоскостями Е=0, а в пространстве за пределами плоскостей.

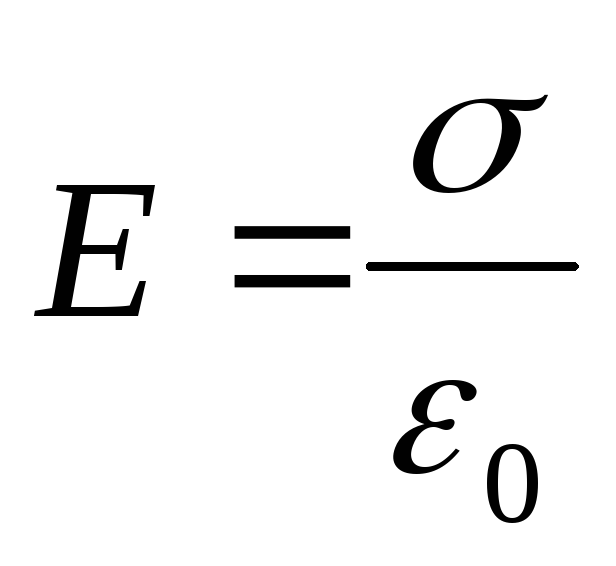Вектором электрической индукции (электрического смещения) D → называют физическую величину, определяемую по системе С И :

D → = ε 0 E → + P → , где ε 0 – электрическая постоянная, E → – вектор напряженности, P → – вектор поляризации.

Вектор электрического смещения в СНС определяется как:

Вектор индукции

Значение вектора D → не является только полевым, потому как он учитывает поляризованность среды. Имеется связь с объемной плотностью заряда, выражаемая соотношением:

По уравнению d i v D → = ρ видно, что для D → единственным источником будут являться свободные заряды, на которых данный вектор начинается и заканчивается. В точках с отсутствующими свободными зарядами вектор электрической индукции является непрерывным. Изменения напряженности поля, вызванные наличием связанных зарядов, учитываются в самом векторе D → .

Связь вектора напряженности и вектора электрического смещения

При наличии изотропной среды запись связи вектора напряженности и вектора электрического смещения запишется как:

D → = ε 0 E → + ε 0 χ E → = ε 0 + ε 0 χ E → = ε ε 0 E → .

Где ε – диэлектическая проницаемость среды.

Наличие D → способствует облегчению анализа поля при наличии диэлектрика. Используя теорему Остроградского-Гаусса в интегральном виде с диэлектриком, фиксируется как:

Проходя через границу разделов двух диэлектриков для нормальной составляющей, вектор D → может быть записан:

D 2 n – D 1 n = σ

n 2 → D 2 → – D 1 → = σ ,

где σ – поверхностная плотность распределения зарядов на границе диэлектриков, n 2 → – нормаль, проведенная в сторону второй среды.

Формула тангенциальной составляющей:

D 2 τ = ε 2 ε 1 D 1 τ .

Единица вектора электрической индукции измеряется в системе С И как К л м 2 .

Поле вектора D → изображается при помощи линий электрического смещения.

Определение направления и густоты идет аналогично линиям вектора напряженности. Но линии вектора электрической индукции начинаются и заканчиваются только на свободных зарядах.

Имеются пластины плоского конденсатора с зарядом q . Произойдет ли изменение вектора электрической индукции при заполненном воздухом пространстве между пластинами и диэлектрика с диэлектрической проницаемостью ε ≠ ε υ o z d .

Поле конденсатора в первом случае характеризовалось вектором смещения ε v o z d = 1 , то есть D 1 → = ε v o z d ε 0 E 1 → = ε 0 E 1 → .

Необходимо заполнить пространство между пластинами конденсатора однородным и изотропным диэлектриком. При наличии поля в конденсаторе диэлектрик поляризуется. Тогда начинают появляться связанные заряды с плотностью σ s υ на его поверхности. Создается дополнительное поле с напряженностью:

Векторы полей E → ‘ и E 1 → имеют противоположные направления, причем:

Запись результирующего поля с диэлектриком примет вид:

E = E 1 – E ‘ = σ ε 0 – σ s υ ε 0 = 1 ε 0 σ – σ s υ .

Формула плотности связанных зарядов:

Произведем подстановку σ s υ = χ ε 0 E в E = E 1 – E ‘ = σ ε 0 – σ s υ ε 0 = 1 ε 0 σ – σ s υ , тогда:

Далее выражаем из ( 1 . 6 ) напряженность поля Е . Формула принимает вид:

E = E 1 1 + χ = E 1 ε .

Отсюда следует, что значение вектора электрической индукции в диэлектрике равняется:

D = ε ε 0 E 1 ε = ε 0 E 1 = D 1 .

Ответ: вектор электрической индукции не изменяется.

Была внесена пластина из диэлектрика с диэлектрической проницаемостью ε без свободных зарядов в зазор между разноименными заряженными пластинами. На рисунке 1 показана при помощи штриховой линии замкнутая поверхность. Определить поток электрической индукции Φ D через эту поверхность.

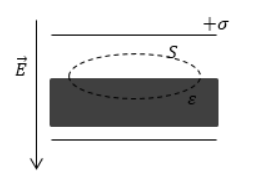
Рисунок 1 . Замкнутая поверхность

Формула записи потока вектора электрического смещения Φ D через замкнутую поверхность S :

Φ D = ∫ S D → · d S → .

Используя теорему Остроградского-Гаусса, можно сказать, что Φ D равняется суммарному свободному заряду, находящемуся внутри заданной поверхности. Из условия видно отсутствие свободных зарядов в диэлектрике и в имеющемся пространстве между пластинами конденсатора, а поток вектора индукции равняется нулю.

Изображена замкнутая поверхность S , проходящая с захватом части пластины изотропного диэлектрика на рисунке 2 . Поток вектора электрической индукции через нее равняется нулю, а поток вектора напряженности > 0 . Какой вывод можно сделать из данной задачи?

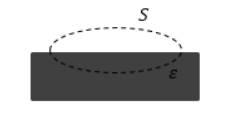
Рисунок 2 . Замкнутая поверхность с захватом части пластины изотропного диэлектрика

Из условия имеем, что поток вектора электрического смещения Φ D через замкнутую поверхность равняется нулю, то есть:

Если использовать теорему Остроградского-Гаусса, то значение Φ D – это суммарный свободный заряд, находящийся внутри заданной поверхности. Следует, что внутри такой поверхности отсутствуют свободные заряды:

Φ D = ∫ S D → · d S → = Q = 0 .

Имеем, что поток вектора напряженности не равен нулю, но он считается как сумма свободных и связанных зарядов. Отсюда вывод – диэлектрик содержит связанный заряды.

Ответ: свободные заряды отсутствуют, а связанные есть, причем с положительной их суммой.

Что такое вектор электрической индукции

Вектором электрической индукции (или вектором электрического смещения) ($overrightarrow$) называют физическую величину, которая определяется в системе СИ как:

где $<varepsilon >_0$ — электрическая постоянная, $overrightarrow$ — вектор напряженность, $overrightarrow

$ — вектор поляризации.

В СГС вектор электрического смещения определен как:

[overrightarrow=overrightarrow+4pi overrightarrow

left(2
ight).]

Вектор $overrightarrow$ не является чисто полевым вектором, так как он учитывает поляризованность среды. Этот вектор связан с объемной плотностью заряда соотношением:

Из (3) мы видим, что единственным источником $overrightarrow$ являются свободные заряды, на которых данный вектор начинается и заканчивается. В точках, где свободные заряды отсутствуют, вектор электрической индукции непрерывен. Изменение напряженности поля, которые вызваны наличием связанных зарядов, учитываются в самом векторе $overrightarrow$.

Связь вектора напряженности и вектора электрического смещения

Связь вектора напряженности и вектора электрического смещения, если среда изотропна, еще можно записать как:

[overrightarrow=left(<varepsilon >_0overrightarrow+<varepsilon >_0varkappa overrightarrow
ight)=left(<varepsilon >_0+<varepsilon >_0varkappa
ight)overrightarrow=varepsilon <varepsilon >_0overrightarrowleft(4
ight),]

Использование вектора $overrightarrow$ существенно облегчает анализ поля при наличии диэлектрика. Так, например теорема Остроградского – Гаусса в интегральном виде при наличии диэлектрика может быть записана как:

При переходе через границу раздела двух диэлектриков для нормальной составляющей вектора $overrightarrow$ можно записать:

где $sigma $ — поверхностная плотность распределения зарядов на границе диэлектриков. $overrightarrow$ — нормаль, которая проведена в сторону второй среды.

Для тангенциальной составляющей:

Единицей измерения в системе СИ вектора электрической индукции служит $frac<Кл><м^2>.$

Поле вектора $overrightarrow$ можно изображать с помощью линий электрического смещения. Направление и густота определяются аналогично линиям вектора напряженности. Однако в отличие от вектора $overrightarrow$ линии вектора электрической индукции начинаются и заканчиваются только на свободных зарядах.

Попробуй обратиться за помощью к преподавателям

Задание: Пластины плоского конденсатора имеют заряд q. Как изменится вектор электрической индукции, если пространство между пластинами сначала было заполнено воздухом, а за тем диэлектриком с диэлектрической проницаемостью $varepsilon
e <varepsilon >_$.

Пусть поле в конденсаторе в первом случае характеризуется вектором смещения ($<varepsilon >_=1$):

Заполним пространство между пластинами конденсатора однородным и изотропным диэлектриком. Под действием поля в конденсаторе диэлектрик поляризуется. На его поверхности появляются связанные заряды с плотностью ($<sigma >_$). Они создают дополнительное поле, напряженность которого равна:

Векторы поля $overrightarrow