Задачи на расчет цепей переменного тока

ОбразЦЫ РЕШЕНИЯ ЗАДАЧ НА РАСЧЕТ ОДНОФАЗНЫХ И ТРЕХФАЗНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА.

Пример решения задачи на расчет неразветленной цепи.

Задача:Последовательно с катушкой, активное сопротивление которой R₁=10 Ом и индуктивность L=0,0318 Гн, включен приемник, обладающий активным сопротивлением R₂=1 Ом и емкостью С=796 мкф (рис. I). К цепи приложено переменное напряжение, изменяющееся по закону u=169,8·sin(314·t).

Определить: полное сопротивление цепи, коэффициент мощности цепи, ток в цепи, активную, реактивную и полную мощности, а также построить в масштабе векторную диаграмму.

Как нужно изменить величину емкости, чтобы в цепи наступил резонанс напряжений? Индуктивность катушки остается постоянной.

Решение:

1. Сравнивая закон изменения напряжения о цепи с общим выражением u=U_M·sin(ωt) , можно заключить, что амплитуда напряжения U_M=169,8 B, а ω=2π·f=314 (1/сек).

Отсюда действующее значение напряжения

2. Индуктивное сопротивление катушки

3. Емкостное сопротивление конденсатора

4. Полное сопротивление цепи

5. Коэффициент мощности цепи

φ=28,35ْ

6. Сила тока в цепи

7. Активная мощность

8. Реактивная мощность

9. Полная мощность

S=I 2 z=9.6 2 ·12.5=1152 ВА

10. Построение векторной диаграммы начинаем с определения потерь напряжений на каждом сопротивлении:

U_R₂

U_R₁

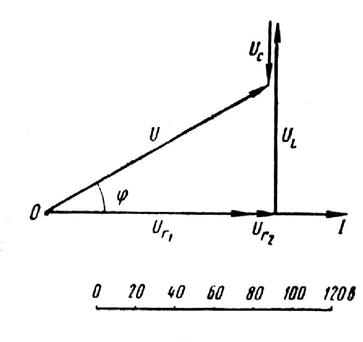
Рис.2

Затем выбираем масштаб для напряжений (см. рис. 2). Построение диаграммы начинаем с вектора тока I, который откладываем по горизонтали вправо от точки О (рис. 2). Вдоль вектора тока откладываем в принятом масштабе напряжения U_R₁ и U_R₂ теряемые в активных сопротивлениях цепи. Эти напряжения совпадают по фазе с током. От конца вектора U_R₂ откладываем в сторону опережения вектора тока под углом 90° вектор потери напряжения U_L в индуктивном сопротивлении. Из конца вектора U_L откладываем вектор U_C в сторону отставания от вектора тока на угол 90 ° . Геометрическая сумма четырех векторов равна полному напряжению, приложенному к цепи, т. е.

11. Для получения резонанса напряжений необходимо, чтобы Х_C=Х_L=10 Ом, тогда , откуда При этом ток в цепи станет , где .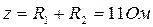

Пример решения задачи на расчет разветвленной цепи.

Задача: Катушка с активным сопротивлением R=20 Oм и индуктивностью L=0,0637 Гн соединена параллельно с конденсатором емкостью С =65 мкФ (рис. 3).

Определить: токи в ветвях и в неразветвленной части цепи, активные мощности ветвей, углы сдвига фаз между током и напряжением первой и второй ветвей и всей цепи, если к цепи приложено напряжение U=100B, частота тока f=50 Гц. Как нужно изменить емкость во второй ветви, чтобы в цепи наступил резонанс токов?

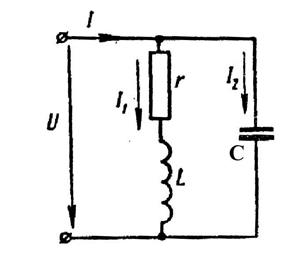
Построить векторную диаграмму.

Решение:

1. Индуктивное сопротивление катушки

2. Емкостное сопротивление конденсатора

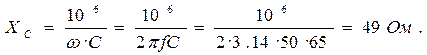
3. Токи в ветвях

4. Коэффициенты мощности ветвей

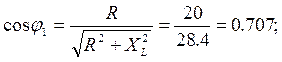
(отстающий)

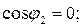
(опережающий).

5. Активные и реактивные составляющие токов ветвей

;

6. Ток в неразвлетвленной части цепи

Реактивные токи ветвей должны вычитаться, так как реактивный ток ветви с емкостью принимается отрицательным.

7. Коэффициент мощности всей цепи

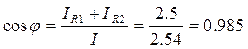
8. Активные мощности ветвей

P₂=0

Построение векторной диаграммы начинаем c вектора напряжения U (рис. 4). Под углом φ₁ к вектору напряжения (в сторону отставания) откладываем вектор тока I₁, под углом φ₂ (в сторону опережения) – вектор тока I₂. Геометрическая сумма этих векторов представляет ток I в неразветвленной части цепи. Проекции токов ветвей на вектор напряжения являются активными составляющими I_R₁ и I_R₂; проекции этих токов на вектор, перпендикулярный вектору напряжения, – реактивными составляющими I_P₁ и I_P₂.

9. При резонансе токов ток I совпадает на фазе с напряжением, что возможно при равенстве реактивных токов ветвей I_P₁=I_P₂ (см. векторную диаграмму (рис.5)).

Расчет электрических цепей переменного синусоидального тока производится в комплексной форме. При этом величины синусоидальных ЭДС и токов представляются в виде комплексных амплитуд или комплексных действующих значений, а все элементы в схеме – в виде комплексных сопротивлений.

Например, если ЭДС источника равна 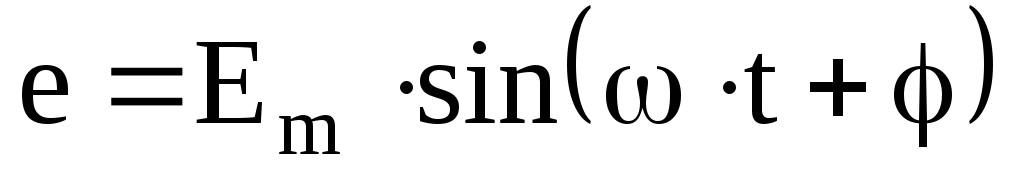, то комплексная амплитуда запишется в виде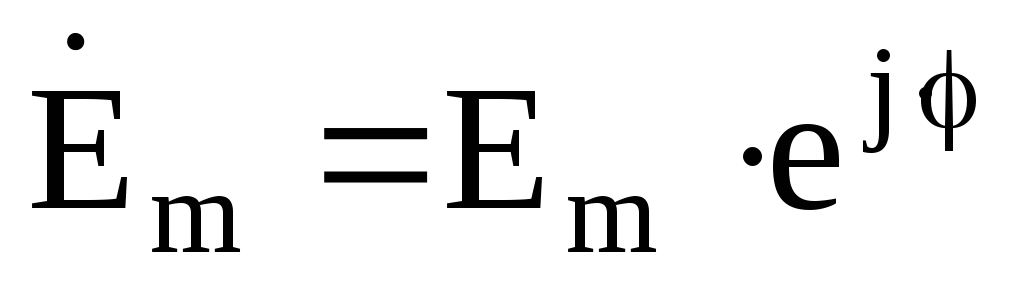– в показательной форме записи, или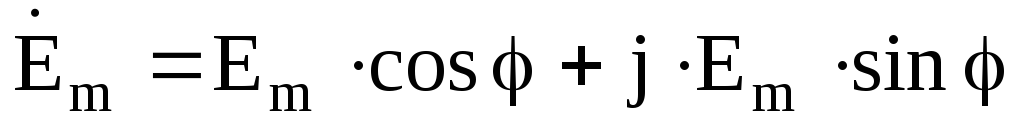– в алгебраической форме. Комплексное действующее значение синусоидальной ЭДС: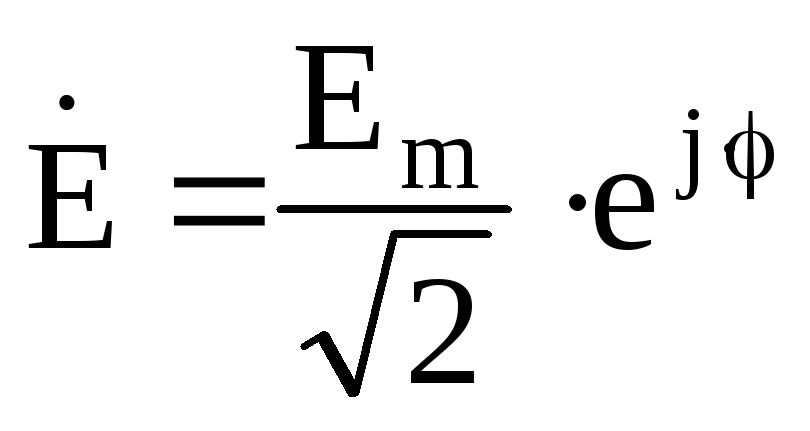– в показательной форме записи, или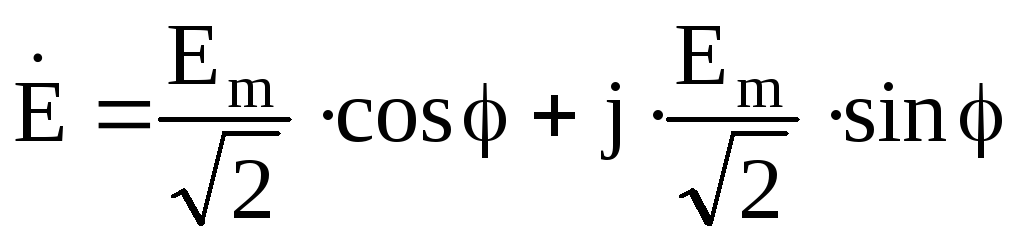– в алгебраической форме.

Комплексные сопротивления элементов электрической цепи переменного тока:

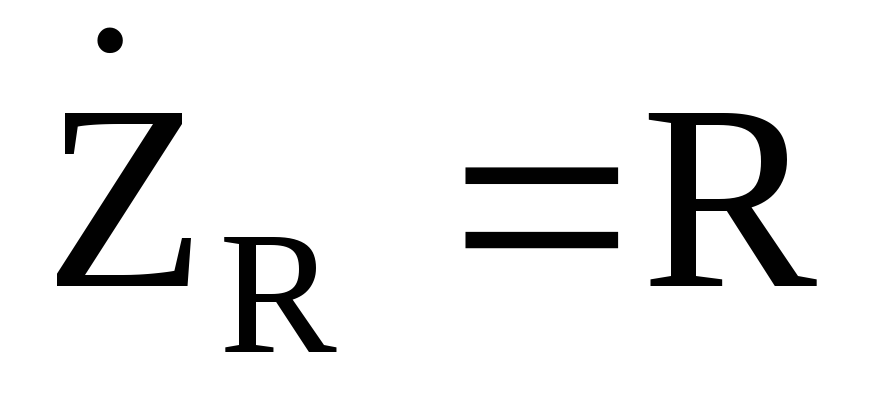– для идеального сопротивления,

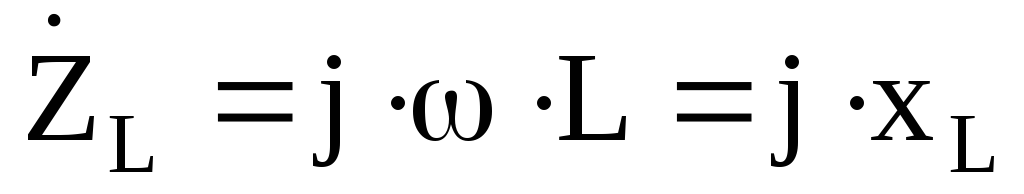– для идеальной индуктивности,

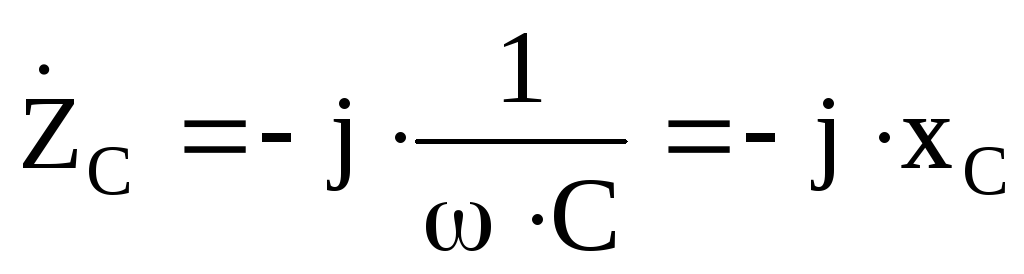– для идеальной емкости.

Далее расчет электрической цепи переменного тока можно вести любым методом, известным из раздела – «электрические цепи постоянного тока». При этом используется математический аппарат, разработанный для операций с комплексными числами.

Применяются три формы записи комплексного значения синусоидальной величины:

– показательная форма,

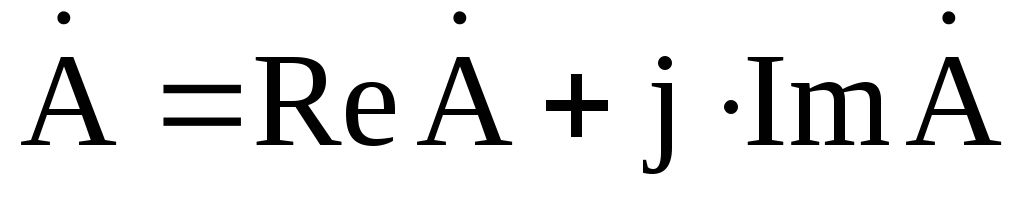– алгебраическая форма,

где 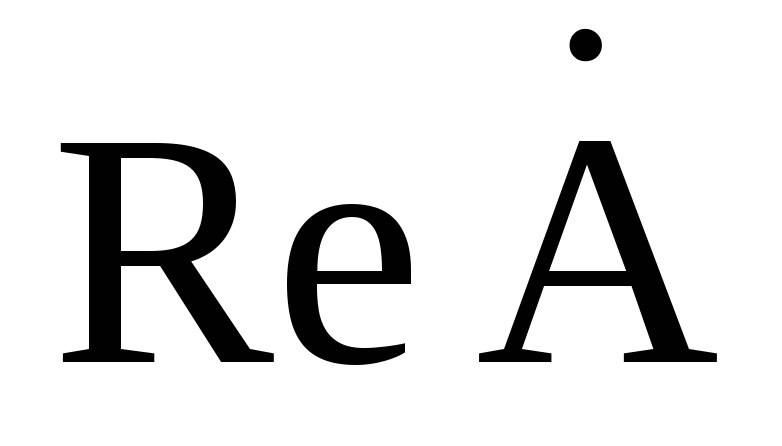и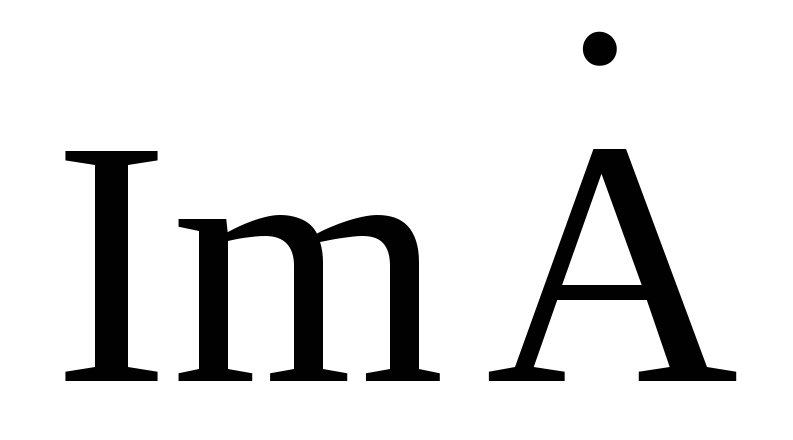– действительная и мнимая часть комплексного значения синусоидальной величины. Переход от алгебраической формы к показательной осуществляется по формулам:

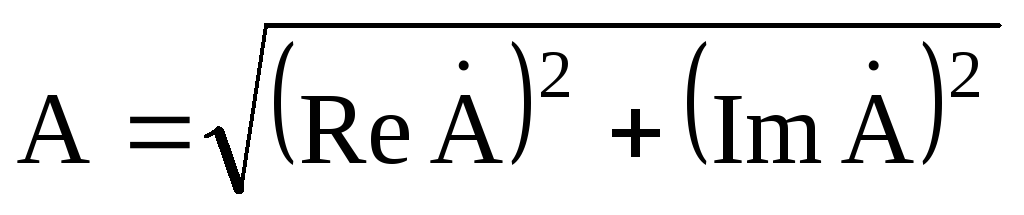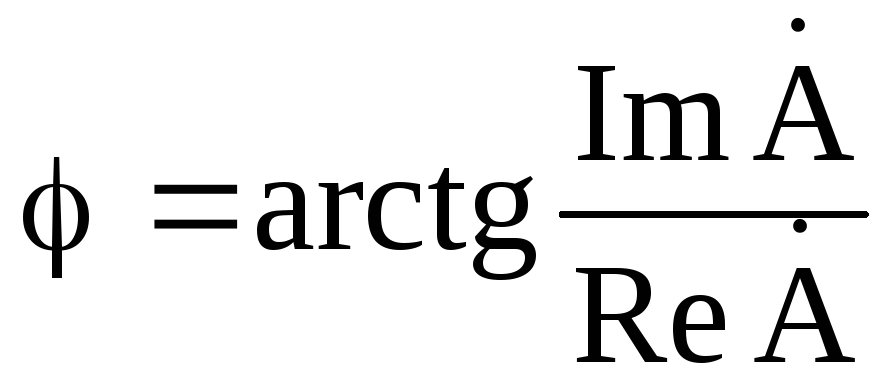Переход от показательной формы к тригонометрической осуществляется по формуле Эйлера:

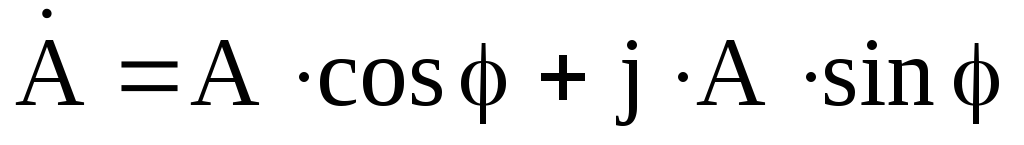Сложение и вычитание комплексных величин производится в алгебраической форме, а умножение и деление в показательной.

При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения синусоидальных величин, сокращенно их называют комплексными значениями.

Расчет однофазных цепей

Р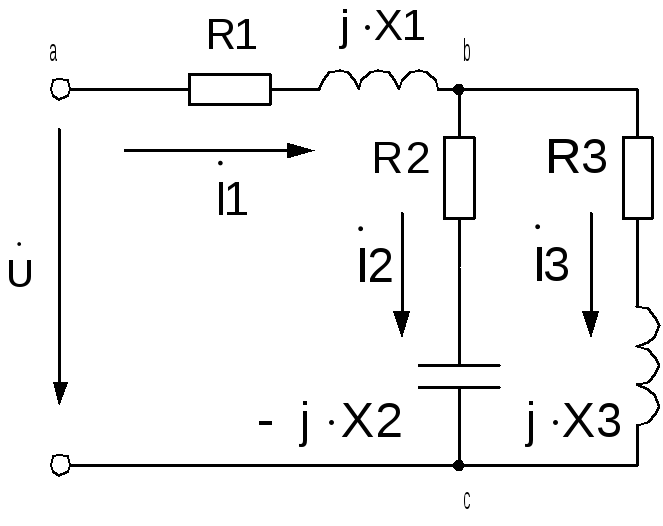асчет однофазных цепей переменного тока при наличии одного источника синусоидальной ЭДС производится методом эквивалентных преобразований. Рассмотрим пример расчета однофазной цепи приведенной на рис.

Рис. 2.4. Схема электрической цепи к примеру расчета

Пример расчета однофазной цепи

По заданным значениям активных и реактивных сопротивлений и напряжению источника определить токи во всех ветвях схемы и падения напряжения на ее участках. Определить комплекс полной мощности, активную и реактивную мощность. Расчет произвести комплексным методом. Выполнить проверку правильности расчета с использованием баланса активных мощностей схемы. Построить векторную диаграмму. Построить мгновенные значения синусоидальных токов ветвей. Исходные данные для расчета приведены в таблице.

В электротехнике большое количество задач посвящено цепям переменного тока . Рассмотрим примеры решения некоторых из них.

Задача 1

В сеть переменного тока включены последовательно катушка индуктивностью 3 мГн и активным сопротивлением 20 Ом и конденсатор емкостью 30 мкФ. Напряжение Uc на конденсаторе 50 В. Определите напряжение на зажимах цепи, ток в цепи, напряжение на катушке, активную и реактивную мощность.

Решение задачи начнём с определения тока в цепи, но для этого нужно сначала определить реактивное сопротивление конденсатора.

Как известно, реактивное сопротивление конденсатора зависит от частоты переменного тока (при её увеличении уменьшается, а при её уменьшении увеличивается), следовательно

Ток в цепи находим из соображения, что элементы в цепи соединены последовательно, а значит, ток на конденсаторе и катушке будет одним и тем же.

Следующим шагом мы определяем индуктивное сопротивление и напряжение катушки

Зная активное сопротивление обмотки катушки, можем определить падение напряжения на нем

Теперь, когда мы знаем напряжение на каждом из элементов, мы можем определить напряжение на зажимах цепи, которое будет равно

Активную мощность в данном случае можно определить как мощность, выделяемую на обмотке катушки

Для определения реактивной мощности необходимо для начала определить угол сдвига ϕ

Так как реактивная мощность имеет отрицательное значение, то цепь имеет емкостной характер.

Задача 2

В цепи как показано на схеме, подключены катушка, конденсатор и резисторы. Индуктивность катушки – 15 мГн, емкость конденсатора 20 мкФ, R1=10 Ом, R2=30 Ом. Напряжение источника 100 В, частота 100 Гц. Определить токи в цепи, активную, реактивную и полную мощность в цепи.