Содержание
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ) , площади поверхности ( S ) , пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ) , единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным ( ( alpha ) ( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ) :
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec ) ЭДС электромагнитной индукции равна:
где ( alpha ) – угол между векторами ( vec ) и ( vec
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ) , создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
В статье расскажем что такое электромагнитная индукция, подробно опишем закон Фарадея и правило Ленца, а так же немного затронем тему уравнений Максвелла.
Электромагнитная индукция
Суть электромагнитной индукции заключается в том, что изменение магнитного поля, покрывающего электрическую цепь, вызывает возникновение электродвижущей силы в этой цепи, которая в случае замкнутой цепи вызывает протекание электрического тока. Если цепь, в которой мы должны генерировать электродвижущую силу, состоит из катушки и прикрепленного к ней амперметра, то источник изменяющегося магнитного поля, который включает в себя катушку, может быть адекватно перемещен постоянным магнитом или движущимся электромагнитом, в котором мы меняем ток питания. В каждом из этих случаев магнитное поле, которое пронизывает катушку, изменяется со временем.
В общем, изменение магнитного потока в цепи амперметра вызывает электрический ток в этой цепи.
Источником индуктивных явлений снова является сила Лоренца F, которая возникает, когда заряд q движется со скоростью v в магнитном поле B
F = q * v * B
Когда направляющая перемещается в поле B, подвижные носители нагрузки будут смещаться под действием силы Лоренца до тех пор, пока в проводнике не появится электрическое поле E, а сила, действующая на носители, F = q * E, уравнивает силу Лоренца. Когда линейный проводник длины l движется с постоянной скоростью v в однородном магнитном поле B, направленном перпендикулярно оси проводника и вектору скорости v , как на чертеже:
тогда мы сохраним условие баланса между силой Лоренца и силой отталкивания между зарядами в виде уравнения:
v*B = E = V / l ,
где V — разность потенциалов на концах проводника длиной l. Следовательно, значение этой разности потенциалов:
Если вектор v не перпендикулярен полю B , но образует с ним угол N , то разность потенциалов на концах направляющей будет:
V = v * B * l * sin θ
Это означает, что перемещение проводника вдоль направления поля B не будет генерировать в нем электродвижущую силу. Нетрудно доказать, что в случае направляющей любой формы разность потенциалов между точками а и b направляющей равна:
Когда прямоугольная рамка со сторонами a и b вращается в однородном магнитном поле B с постоянной угловой скоростью T
это электродвижущая сила V, генерируемая с обеих сторон рамы:
Магнитные силы, действующие в двух других сторонах петли, перпендикулярны этим сторонам и не влияют на электродвижущую силу. Посредством соответствующего способа получения генерируемого напряжения можно реализовать простейшие модели генераторов переменного тока (а) и постоянного тока (b), как показано на рисунке:
В природе и технике существует огромное количество явлений, вызванных электромагнитной индукцией, то есть генерацией электродвижущей силы в пространстве, где существует изменяющееся магнитное поле. Все эти явления описываются одним замечательным, компактным уравнением, являющимся содержанием закона Фарадея.
Формулы и объяснение закона Фарадея
Большое открытие Майкла Фарадея (1791 — 1867) состояло в том, что он нашел правило, управляющие электромагнитной индукцией. В результате многолетних экспериментов Фарадей заявил, что электродвижущая сила E появляется в проводнике при изменении магнитного поля, окружающего этот проводник, величина генерируемой электродвижущей силы пропорциональна скорости магнитного поля, и что направление индуцированной электродвижущей силы зависит от направления, в котором изменяется магнитное поле. Все эти факты содержатся только в одном уравнении:
где dΦ B — элементарный поток магнитного поля
В общем случае, даже когда проводников нет, электродвижущая сила равна циркуляции электрического поля E вдоль замкнутого контура:
Таким образом , закон Фарадея может быть записан в обобщенной форме:
Обратите внимание, сколько факторов может изменить значение потока:
1. Изменение значения вектора B ;
2. Изменение значения площади поверхности d A ;
3. Путем изменения угла между B и d А ;
4. Одновременное изменение B и d А ;
5. Одновременное изменение В и угла ;
6. Одновременное изменение d A и угла.
Нельзя не заметить появившийся здесь знак минус! Этот знак минус в законе Фарадея был назван правилом Ленца, который можно понимать как правило неповиновения в электродинамике.
Правило Ленца
Правило Ленца (знак минуса в законе Фарадея) определяет, что индукционный электрический ток в проводнике, возникающий при изменении магнитного потока, направлен таким образом, что его магнитное поле противодействует изменению магнитного потока.
Закон индукции Фарадея вместе с правилом Ленца представляет собой анимацию, в которой движение постоянного магнита вызывает создание электродвижущей силы в катушке, покрытой полем магнита.
Индукционный ток может создаваться не только в обмотках, но и в сплошных металлических блоках, помещенных в изменяющиеся магнитные поля.
Пример: так называемый вихревой ток, схематически показанный на рисунке:
Когда постоянное магнитное поле приложено к вращающейся алюминиевой мишени, то в мишени создаются два семейства противоположно направленных токов. Магнитное поле вихревых токов направлено так, что часть диска, которая выходит из поля, будет втянута обратно в поле, а часть диска, которая входит в область поля, будет вытеснена из этого поля.
Вихревые токи часто нежелательны, например, в сердечниках трансформатора, где они вызывают потери тепла. Для ограничения вихревых токов сердечники трансформатора выполнены в виде стопок из листового металла.
Уравнения Максвелла в интегральной форме
Закон Фарадея содержит: обобщенный закон Ампера, закон Гаусса для электрического поля и закон Гаусса для магнитного поля в системе из четырех уравнений Максвелла. Эти уравнения были представлены применительно к макроскопическим контурам и замкнутым поверхностям. По этой причине мы говорим, что это уравнения Максвелла в интегральной форме. Давайте посмотрим на эти уравнения еще раз.
Закон Фарадея
Обобщенный закон Ампера
Закон Гаусса для электрического поля
Закон Гаусса для магнитного поля
Интегральные уравнения Максвелла описывают электрические и магнитные явления в макроскопическом масштабе. Ведь для их формулировки нужны контуры, замкнутые поверхности, токи и потоки полей. Однако чрезвычайно важно знать, что происходит с электрическими и магнитными полями в отдельных точках, то есть в микроскопическом масштабе. Тогда можно будет описать такие явления как электромагнитные волны.
Для микроскопического описания электрических и магнитных явлений используются уравнения Максвелла в дифференциальной форме. Чтобы получить их, мы применим две математические теоремы к уравнениям в интегральной форме: теорема Гаусса-Остроградского и теорема Стокса.
Следует отметить, что преобразование уравнений Максвелла между целочисленной и дифференциальной формами получается в результате только математических операций. Это означает физическую эквивалентность этих двух форм уравнений Максвелла.
Теорема Гаусса-Остроградского и теорема Стокса, несмотря на их кажущуюся сложность, концептуально совершенно просты и легко интуитивно принимаются. Обе эти тему будут представлены в следующей статье.
Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
Что может быть лучше, чем вечером понедельника почитать про основы электродинамики. Правильно, можно найти множество вещей, которые будут лучше. Тем не менее, мы все равно предлагаем Вам прочесть эту статью. Времени занимает не много, а полезная информация останется в подсознании. Например, на экзамене, в условиях стресса, можно будет успешно извлечь из недр памяти закон Фарадея. Так как законов Фарадея несколько, уточним, что здесь мы говорим о законе индукции Фарадея.
Электродинамика – раздел физики, изучающий электромагнитное поле во всех его проявлениях.
Это и взаимодействие электрического и магнитного полей, электрический ток, электро-магнитное излучение, влияние поля на заряженные тела.
Здесь мы не ставим целью рассмотреть всю электродинамику. Упаси Боже! Рассмотрим лучше один из основных ее законов, который называется законом электромагнитной индукции Фарадея.
Майкл Фарадей (1791-1867)
История и определение
Фарадей, параллельно с Генри, открыл явление электромагнитной индукции в 1831 году. Правда, успел опубликовать результаты раньше. Закон Фарадея повсеместно используется в технике, в электродвигателях, трансформаторах, генераторах и дросселях. В чем суть закона Фарадея для электромагнитной индукции, если говорить просто? А вот в чем!
При изменении магнитного потока через замкнутый проводящий контур, в контуре возникает электрический ток. То есть, если мы скрутим из проволоки рамку и поместим ее в изменяющееся магнитное поле (возьмем магнит, и будем крутить его вокруг рамки), по рамке потечет ток!
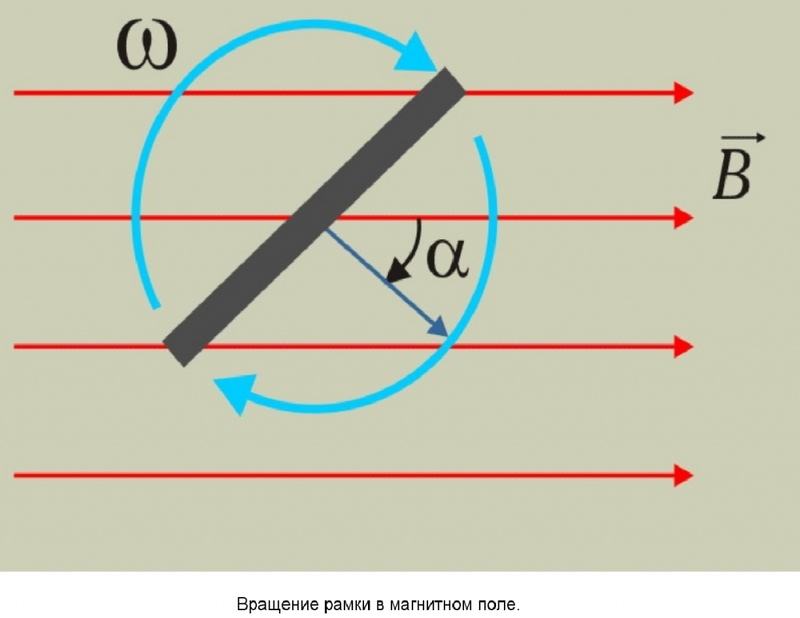Рамка в поле
Этот ток Фарадей назвал индукционным, а само явление окрестил электромагнитной индукцией.
Электромагнитная индукция – возникновение в замкнутом контуре электрического тока при изменении магнитного потока, проходящего через контур.
Формулировка основного закона электродинамики – закона электромагнитной индукции Фарадея, выглядит и звучит следующим образом:
ЭДС, возникающая в контуре, пропорциональна скорости изменения магнитного потока Ф через контур.
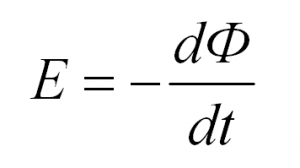
А откуда в формуле минус, спросите Вы. Для объяснения знака минус в этой формуле есть специальное правило Ленца. Оно гласит, что знак минус, в данном случае, указывает на то, как направлена возникающая ЭДС. Дело в том, что создаваемое индукционным током магнитное поле направлено так, что препятствует изменению магнитного потока, который вызвал индукционный ток.
Для определения направления индукционного тока применяется знаменитое правило буравчика, или правило правой руки, оно же правило правого винта. Если ладонь правой руки расположить так, чтобы в неё входили силовые линии магнитного поля, а отогнутый большой палец направить по движению проводника, то четыре вытянутых пальца укажут направление индукционного тока.
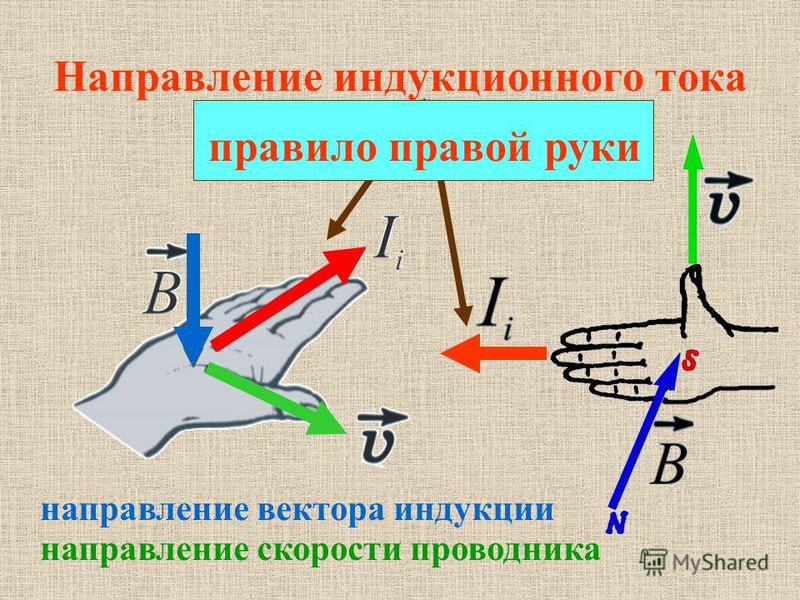Правило правой руки
Примеры решения задач
Вот вроде бы и все. Значение закона Фарадея фундаментально, ведь на использовании данного закона построена основа почти всей электрической промышленности. Чтобы понимание пришло быстрее, рассмотрим пример решения задачи на закон Фарадея.
И помните, друзья! Если задача засела, как кость в горле, и нет больше сил ее терпеть – обратитесь к нашим авторам! Теперь вы знаете где заказать курсовую работу. Мы быстро предоставим подробное решение и разъясним все вопросы!