Содержание
Закон Кирхгофа (правила Кирхгофа), сформулированные Густавом Кирхгофом в 1845 году, являются следствиями из фундаментальных законов сохранения заряда и безвихревости электростатического поля.
Закон Кирхгофа – это соотношения, выполняемые между токами и напряжениями на участках любых электрических цепей. Они позволяют рассчитывать любые электрические цепи: постоянного, переменного или квазистационарного тока.
При формулировании правил Кирхгофа используют такие понятия, как ветвь, контур и узел электрической цепи.
- Ветвь – участок электрической цепи с одни и тем же током.
- Узел – точка соединения трех или более ветвей.
- Контур – замкнутый путь, проходящий через несколько узлов и ветвей разветвлённой электрической цепи.
При обходе надо учесть, что ветвь и узел могут одновременно принадлежать нескольким контурам. Правила Кирхгофа справедливы как для линейных, так и для нелинейных цепей при любом характере изменения во времени токов и напряжений. Правила Кирхгофа широко применяются при решении задач электротехники за счет легкости в расчетах.
1 закон Кирхгофа
В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, сопротивлением и ЭДС всей цепи или на каком-либо участке цепи определяются законом Ома. Но на практике в цепях токи от какой-либо точки идут по разным путям (Рис. 1). Поэтому становиться актуальным введение новых правил для проведения расчетов электрических цепей.
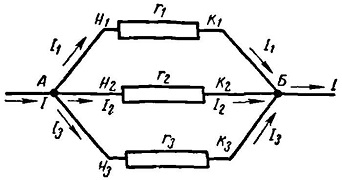
Рис. 1. Схема параллельного соединения проводников.
Так, при параллельном соединении проводников начала всех проводников соединены в одну точку, а концы проводников – в другую точку. Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.
Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А, растекается далее по трем сопротивлениям и равен сумме токов, выходящих из этой точки: I = I1 + I2 + I3.
Согласно первому правилу Кирхгофа алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла – отрицательным.
Запишем первый закон Кирхгофа в комплексной форме:
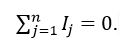
Первый закон Кирхгофа гласит, что алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла. То есть, сколько тока втекает в узел, столько же вытекает (как следствие закона сохранения электрического заряда). Алгебраическая сумма – это сумма, в которую входят слагаемые со знаком плюс и со знаком минус.

Рис. 2. i_1+i_4=i_2+i_3.
Рассмотрим применение 1 закона Кирхгофа на следующем примере:

- I1 – это полный ток, текущий к узлу А, а I2 и I3 — токи, вытекающие из узла А.
- Тогда мы можем записать: I1 = I2 + I3.
- Аналогично для узла B: I3 = I4 + I5.
- Пусть, что I4 = 5 А и I5 = 1 А, получим: I3 = 5 + 1 = 6 (А).
- Пусть I2 = 10 А, получим: I1 = I2 + I3 = 10 + 6 = 16 (А).
- Запишем подобное соотношение для узла C: I6 = I4 + I5 = 5 + 1 = 6 А.
- А для узла D: I1 = I2 + I6 = 10 + 6 = 16 А
- Таким образом мы наглядно видим справедливость первого закона Кирхгофа.
2 закон Кирхгофа
При расчете электрических цепей в большинстве случаев нам встречаются цепи, образующие замкнутые контуры. В состав таких контуров, кроме сопротивлений, могут входить ЭДС (источники напряжений). На рисунке 4 представлен участок такой электрической цепи. Произвольно выбираем положительные направления токов. Обходим контур от точки А в произвольном направлении (выберем по часовой стрелке). Рассмотрим участок АБ: происходит падение потенциала (ток идет от точки с высшим потенциалом к точке с низшим потенциалом).

- На участке АБ: φА + E1 – I1r1 = φБ.
- БВ: φБ – E2 – I2r2 = φВ.
- ВГ: φВ – I3r3 + E3 = φГ.
- ГА: φГ – I4r4 = φА.
- Складывая данные уравнения, получим: φА + E1 – I1r1 + φБ – E2 – I2r2 + φВ – I3r3 + E3 + φГ – I4r4 = φБ + φВ + φГ + φА
- или: E1 – I1r1 – E2 – I2r2 – I3r3 + E3 – I4r4 = 0.
- Откуда имеем следующее: E1 – E2 + E3 = I1r1 + I2 r2 + I3r3 + I4r4.
Таким образом, получаем формулу второго закона Кирхгофа в комплексной форме:
Уравнение для постоянных напряжений – 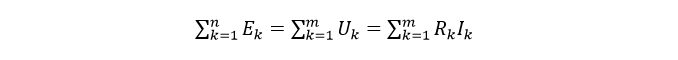 Уравнение для переменных напряжени –
Уравнение для переменных напряжени – 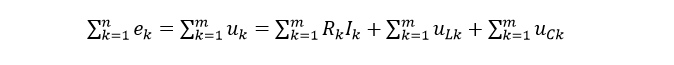
Теперь можем сформулировать определение 2 (второго) закона Кирхгофа:
Второй закон Кирхгофа гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура, равна алгебраической сумме ЭДС, входящих в этот контур. В случае отсутствия источников ЭДС, суммарное напряжение равно нулю.

Иначе формулируя второе правило Кирхгофа, можно сказать: при полном обходе контура потенциал, изменяясь, возвращается к начальному значению.
При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура, при этом падение напряжения на ветви считается положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, в противном случае – отрицательным.
Определить знак можно по алгоритму:
- 1. выбираем направление обхода контура (по или против часовой стрелки);
- 2. произвольно выбираем направления токов через элементы цепи;
- 3. расставляем знаки для напряжений и ЭДС по правилам (ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура со знаком «+», иначе – «-»; напряжения, падающие на элементах цепи, если ток, протекающий через эти элементы совпадает по направлению с обходом контура, со знаком «+», в противном случае – «-»).
Закон Ома является частным случаем второго правила для цепи.
Приведем пример применения второго правила Кирхгофа:

По данной электрической цепи (Рис 6) необходимо найти ее ток. Произвольно берем положительное направление тока. Выберем направление обхода по часовой стрелке, запишем уравнение 2 закона Кирхгофа:

Знак минус означает, что выбранное нами направление тока противоположно его действительному направлению.
Решение задач
1. По приведенной схеме записать законы Кирхгофа для цепи.

| Дано: | Решение: |
|---|---|
|
|
2. На рисунке приведена цепь с двумя источниками ЭДС величиной 12 В и 5 В, с внутренним сопротивлением источников 0,1 Ом, работающих на общую нагрузку 2 ома. Как будут распределены токи в этой цепи, какие они имеют значения?.
Два приема, которые применяют для упрощения процесса составления уравнений, необходимых при расчетах сложных разветвленных цепей постоянного тока называют законами (вернее было бы сказать правилами) Кирхгофа. Прежде чем перейти к самим правила Кирхгофа введем два необходимых определения.
Разветвлёнными цепями названы цепи, которые имеют несколько замкнутых контуров, несколько источников электродвижущей силы (ЭДС).
Узлом разветвлённой цепи называют точку, в которой сходятся три или более проводников с токами.
Первый закон (правило) Кирхгофа, простыми словами
Первое правило Кирхгофа называют правилом узлов, так как оно касается сил токов в узах цепи. Словесно первый закон Кирхгофа формулируют следующим образом: Алгебраическая сумма сил токов в узле равна нулю. В виде формулы это правило запишем как:
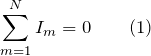
С каким знаком сила тока будет входить в сумму (1), зависит от произвольного выбора. Но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки. Пусть все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными. Если направления токов изначально не заданы, то их задают произвольно. Если при расчетах получено, что сила тока отрицательна, значит, что верное направление тока является противоположным тому, которое предполагали.
Первый закон Кирхгофа является следствием закона сохранения заряда. Если в цепи текут только постоянные токи, то нет в этой цепи точек, которые накапливали бы заряд. Иначе токи не были бы постоянными.
Первый закон Кирхгофа дает возможность составить 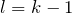 независимое уравнение, при наличии в цепи k узлов.
независимое уравнение, при наличии в цепи k узлов.
Второй закон (правило) Кирхгофа, простыми словами
Второй закон Кирхгофа относят к замкнутым контурам, поэтому его называют правилом контуров. Согласно этому правилу суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних ЭДС ( ), входящих в рассматриваемый контур. В виде формулы второй закон Кирхгофа запишем как:
), входящих в рассматриваемый контур. В виде формулы второй закон Кирхгофа запишем как:
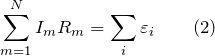
где величину 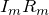 часто называют падением напряжения; N – число рассматриваемых участков избранного контура. При использовании второго правила Кирхгофа важно помнить о направлении обхода контура. Как это делается? Произвольно выберем направление обхода рассматриваемого в задаче контура (по часовой стрелке или против нее). В случае совпадения направления обхода контура с направлением силы тока в рассматриваемом элементе, величина
часто называют падением напряжения; N – число рассматриваемых участков избранного контура. При использовании второго правила Кирхгофа важно помнить о направлении обхода контура. Как это делается? Произвольно выберем направление обхода рассматриваемого в задаче контура (по часовой стрелке или против нее). В случае совпадения направления обхода контура с направлением силы тока в рассматриваемом элементе, величина 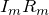 входит в (2) со знаком плюс. ЭДС войдет в сумму правой части выражения (2) со знаком плюс, если при движении вдоль контура, в соответствии с избранным направлением обхода первым мы встречаем отрицательный полюс источника ЭДС.
входит в (2) со знаком плюс. ЭДС войдет в сумму правой части выражения (2) со знаком плюс, если при движении вдоль контура, в соответствии с избранным направлением обхода первым мы встречаем отрицательный полюс источника ЭДС.
Используя второе правило Кирхгофа можно получить независимые уравнения для тех контуров цепи, которые не получены наложением уже описанных контуров. Количестов независимых контуров (n) равно:
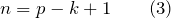
где p – количество ветвей в цепи; k – число узлов.
Количество независимых уравнений, которые дадут оба правила Кирхгофа равно (s):
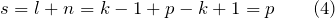
Делаем вывод о том, что число независимых уравнений будет равно числу разных токов в исследуемой цепи.
Второе правило Кирхгофа — следствие закона Ома. В принципе любую цепь можно рассчитать, применяя только закон Ома и закон сохранения заряда. Правила Кирхгофа являются всего лишь упрощающими приемами для решения задач, рассматривающих цепи постоянного тока.
Используя правила Кирхгофа для составления уравнений необходимо внимательно следить за расстановкой знаков токов и ЭДС.
Первое и второе правила Кирхгофа дают метод расчета цепи, то есть используя их можно найти все токи в цепи, если известны все ЭДС и сопротивления, в том числе и внутренние сопротивления источников.
Примеры решения задач
| Задание | Как следует записать уравнение для токов, используя первое правило Кирхгофа для узла А, изображенного на рис.1 |
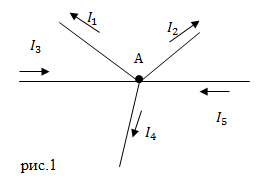

Из узла А выходят токи:
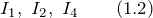
Тогда согласно правилу узлов имеем:
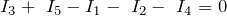
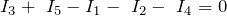
| Задание | Составьте систему независимых уравнений, используя правила Кирхгофа, которая позволит найти все токи в цепи, представленной на рис.2, если известны все ЭДС и все сопротивления (они указаны на рисунке)? |
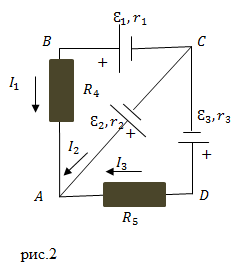
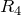 течет ток
течет ток 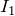 . На рис.2 видно, что в нашей цепи два узла. Это точки A и С. Запишем первое правило Кирхгофа для узла А:
. На рис.2 видно, что в нашей цепи два узла. Это точки A и С. Запишем первое правило Кирхгофа для узла А:
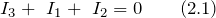
Так как узлов всего два, то первое правило Кирхгофа даст нам только одно независимое уравнение (2.1).
Контуров в подставленной цепи три. Втрое правило Кирхгофа даст нам два независимых уравнения. Рассмотрим контуры ABCA и ACDA. Направлением обхода выберем движение против часовой стрелки. Тогда для контура ABCA имеем:
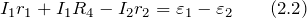
Для контура ACDA получим:
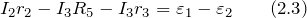
Получили систему из трех независимых уравнений для трех неизвестных токов:
Густав-Роберт Киргоф, выдающийся немецкий физик и математик позапрошлого века, открыл и сформулировал два электротехнических закона, названных в его честь.

Открытия Кирхгоффа
При всей видимой простоте и понятности, законы Кирхгофа стали фундаментальными основами современной науки и базой для методов схематических расчетов. Их практическое значение трудно переоценить. Базой для научных изысканий профессора Кирхгофа стали законы сохранения заряда и энергии, открытые ранее. Некоторые специалисты считают, что правильнее называть описанные Кирхгоффом закономерности правилами, чтобы не путать их с другими замечательными открытиями этого физика, касающимися способностей тел излучать и поглощать энергию, а также зависимости скорости протекания химических реакций от температуры. Однако в научной и технической литературе принято все же пользоваться термином «закон Кирхгофа», тем самым подчеркивая заслуги этого великого ученого в области электротехники. Итак, их два.
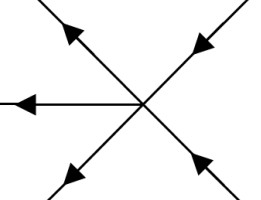
1. Закон Кирхгофа о токах в узлах
Узлами в электротехнике называют точки соединения проводников в количестве не менее трех. Для того чтобы понять действие Первого закона Киргофа, достаточно представить себе обычный водопроводный тройник. Если в одну из труб подается вода, то в две остальные она вытекает. Возможен и другой вариант, когда отводная труба одна, а приточных две, но в любом случае, сколько воды в тройник затечет, столько же и вытечет. Теперь задачу можно усложнить, допустив, что количество входов и выходов в узле сколь угодно большое. Однако результат будет тот же, количество поступающей и уходящей жидкости будет равным, то есть, говоря языком математики, алгебраическая сумма расходов равна нулю. Первый закон Кирхгофа рассматривает электрические токи в узлах, которые ведут себя так же, как и вода в тройнике. Если есть входящие и выходящие токи, то их сумма с учетом знака будет нулевой. При этом величина входящих токов обозначается положительным знаком «плюс», а выходящих – отрицательным «минус». Математическая формула выглядит примерно так:
где I вх. – величины входящих токов со знаком «+»;
I вых. – величины выходящих токов со знаком «-».
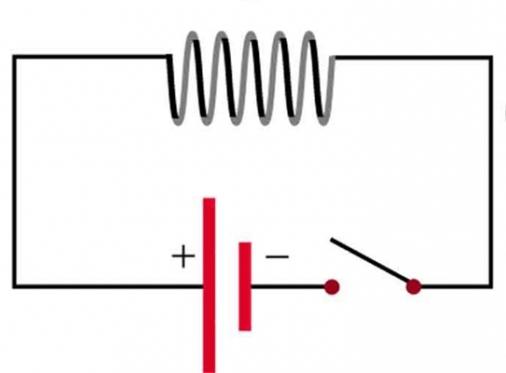
2. Закон Кирхгофа о сумме падений напряжений
Второй закон Кирхгофа понять несколько сложнее, у него нет столь прямых и наглядных ассоциаций как у первого, тем не менее, он тоже несложен. Для начала следует представить себе замкнутую простейшую электрическую цепь, состоящую из источника питания и активной нагрузки в виде сопротивления. При замыкании клемм выключателя через резистор пойдет ток, и все подаваемое напряжение на нем же упадет. Задача вновь усложняется, и количество сопротивлений изменяется. Теперь их много, и у всех разная величина. При прохождении через них электрического тока он будет в цепи одинаковым и, согласно закону Ома, равен напряжению источника, поделенному на сумму всех сопротивлений. На каждом из них будет падать его часть. Так вот, Второй закон Кирхгофа гласит, что общая сумма падений напряжений на каждом из участков цепи равна величине напряжения питания. Говоря иными словами, общая алгебраическая сумма вместе с источником равна нулю.
Простейшая математическая формула описывает Второй закон Кирхгофа следующим образом:
где U ц – падения напряжений на разных участках замкнутой электрической цепи (контура).




