Содержание
Если в проводящей среде выделить некоторый объем, по которому протекает постоянный, не изменяющийся во времени ток, то можно сказать, что ток, который войдет в объем, должен равняться току, вышедшему из него, иначе в этом объеме происходило бы накопление зарядов, что не подтверждается опытом. Сумму входящего в объем и выходящего из объема токов записывают так:

Равенство останется справедливым, если обе его части разделить на объем:

Очевидно, что последнее соотношение будет справедливо и в том случае, если объем, находящийся внутри замкнутой поверхности, устремить к нулю:

Таким образом, для постоянного, неизменного во времени поля в проводящей среде
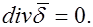 |
(42.6) |
Это соотношение называют первым законом Кирхгофа в дифференциальной форме. Оно означает, что в установившемся режиме в любой точке поля нет ни истока, ни стока линий тока проводимости.
Уравнение Лапласа для электрического поля в
Проводящей среде
Напряженность электрического поля в проводящей среде, как и в электростатическом поле,  .
.
В неизменном во времени поле
 |
(42.7) |
Если среда однородна и изотропна (γ=const), то  можно вынести за знак дивиргенции и, следовательно,
можно вынести за знак дивиргенции и, следовательно,
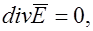 |
(42.8) |
 . . |
(42.9) |
Таким образом, поле в однородной проводящей среде подчиняется уравнению Лапласа. Поле постоянного тока в проводящей среде является полем потенциальным. В нем, в областях, не занятых источниками, 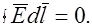
6. Переход тока из среды с проводимостью γ1 в среду с
проводимостью γ2. Граничные условия
Выясним, какие граничные условия выполняются при переходе тока из среды с одной проводимостью в среду с другой проводимостью.
 Возьмем на границе раздела сред – линия 00 (рис. 42.2) замкнутый контур 1234. Составим циркуляцию вектора
Возьмем на границе раздела сред – линия 00 (рис. 42.2) замкнутый контур 1234. Составим циркуляцию вектора 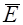 вдоль этого контура. Стороны 12 и 34 его весьма малы по сравнению со сторонами 23 и 41 (длину последних обозначим dl).
вдоль этого контура. Стороны 12 и 34 его весьма малы по сравнению со сторонами 23 и 41 (длину последних обозначим dl).
Так как 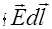 вдоль любого замкнутого контура равен нулю, то он равен нулю и для контура 12341.
вдоль любого замкнутого контура равен нулю, то он равен нулю и для контура 12341.
В силу малости отрезков 12 и 34 пренебрежем составляющими интеграла вдоль этих путей и тогда
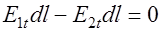 или или 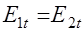 , , |
(42.10) |
т.е. на границе раздела равны тангенциальные составляющие напряженности поля.
На границе раздела равны нормальные составляющие плотностей токов. Докажем это.
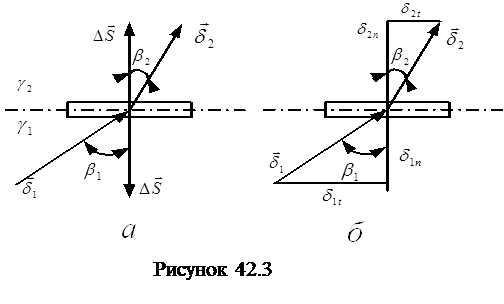 |
На границе раздела выделим сплющенный параллелепипед (рис. 42.3,а). Поток вектора  , втекающий в объем через нижнюю грань, равен
, втекающий в объем через нижнюю грань, равен  ; поток вектора
; поток вектора  , вытекающий из объема через верхнюю грань
, вытекающий из объема через верхнюю грань  . Так как
. Так как 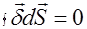 , то
, то
 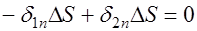 ; ;  . . |
(42.11) |
Следовательно, при переходе тока из среды с одной проводимостью в среду с другой проводимостью непрерывна тангенциальная составляющая вектора 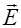 , то есть
, то есть 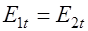 (но
(но  ), и непрерывна нормальная составляющая плотности тока
), и непрерывна нормальная составляющая плотности тока  (но
(но  ).
).
Отсюда следует, что полные значения вектора 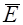 и вектора
и вектора 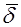 в общем случае меняются скачком на границе раздела.
в общем случае меняются скачком на границе раздела.
Найдем связь между углом падения 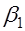 и углом преломления
и углом преломления 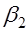 . В соответствии с рис. 42.3,б:
. В соответствии с рис. 42.3,б:
 ; ; 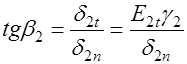 или или 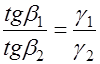 . . |
(42.12) |
Если ток переходит из среды с большой проводимостью (например, из металла) в среду с малой (например, в землю), то тангенс угла преломления 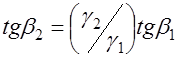 меньше тангенса угла падения и, следовательно, угол
меньше тангенса угла падения и, следовательно, угол 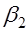 меньше угла
меньше угла 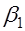 . Если
. Если 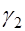 весьма мало, то угол
весьма мало, то угол 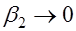 .
.
Вопросы для самоконтроля
1. Какой ток называют током проводимости , а какой – током смещения?
2. Как связаны вектор плотности тока и ток?
3. Проделайте вывод закона Ома в дифференциальной форме.
4. Что понимают под сторонней напряженностью электрического поля?
5. Почему уравнение  называют обобщенным законом Ома, а также вторым законом Кирхгофа?
называют обобщенным законом Ома, а также вторым законом Кирхгофа?
6. Проделайте вывод первого закона Кирхгофа в дифференциальной форме и поясните его физический смысл.
7. Получите выражение для закона Джоуля-Ленца в дифференциальной форме.
8. Докажите, что электрическое поле в проводящей среде подчиняется уравнению Лапласа.
9. Сформулируйте условия на границе раздела двух сред с разной удельной проводимостью.
Дата добавления: 2017-03-11 ; просмотров: 572 | Нарушение авторских прав
Закон Кирхгофа связывает между собой параметры, связанные с тепловым излучением тел. Такие как монохроматический коэффициент поглощения (поглощательная способность) ($A_<
u ,T>$) и спектральная плотность энергетической светимости тела ($E_<
u ,T>$). Напомню, что коэффициент $A_<
u ,T> $ определяется как:
где $dW_
Выражение, определяющее величину $E_<
u ,T>$ имеет вид:
где $dW$- энергия теплового излучения единицы площади поверхности тела, в единицу времени при частоте, которая находится в интервале от $
u $ до $
u $+d$
u $.
Дифференциальная форма закона Кирхгофа
Между вышеназванными величинами для любого непрозрачного тела существует соотношение, которое называют законом Кирхгофа. В дифференциальной форме он имеет следующий вид:
Попробуй обратиться за помощью к преподавателям
где $<varepsilon >_<
u ,T >$– излучательная способность абсолютно черного тела. Уравнение (3) показывает, что для любой температуры и частоты отношение излучательной способности тела к его поглощательной способности одинаково для любых тел и равно излучательной способности черного тела. $<varepsilon >_<
u ,T >=<varepsilon >_<
u ,T >(
u ,T)$ – функция частоты и температуры ее еще называют функцией Киргхофа.
Из закона Кирхгофа следует, что если в данном интервале частот $A_<
u ,T>=0$, то есть тело не поглощает излучение, то $E_<
u ,T>=0$, то есть тело в этом же интервале частом не может и излучать. Чем больше тело излучает, на какой – то определенной частоте, тем больше поглощает на той же частоте. Наибольшее излучение при заданной температуре у абсолютно черного тела.
Интегральная форма закона Кирхгофа
Прежде, чем записать закон Кирхгофа в интегральной форме введем еще несколько необходимых физических величин, которые характеризует тепловое излучение тела. Интегральная излучательная способность (энергетическая светимость) тела ($E_T$) равна поверхностной плотности мощности теплового излучения тела. Математически определение $E_T$ записывается как:
где $E_<lambda ,T>=frac<с><<lambda >^2>E_<
u ,T>$ – излучательная способность тела. $E_T$ также называют энергией излучения всех возможных частот, которые испускаются с единицы поверхности тела на единицу времени. Интегральная излучательная способность ($<varepsilon >_$) — абсолютно черного тела равна:
Соотношение между интегральной излучательной способностью серого тела ($
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Уфимский государственный авиационный технический университет
Расчетно-графическая работа №2
Анализ электрической цепи переменного тока
Порядок выполнения работы:
Анализ электрической цепи синусоидального тока.
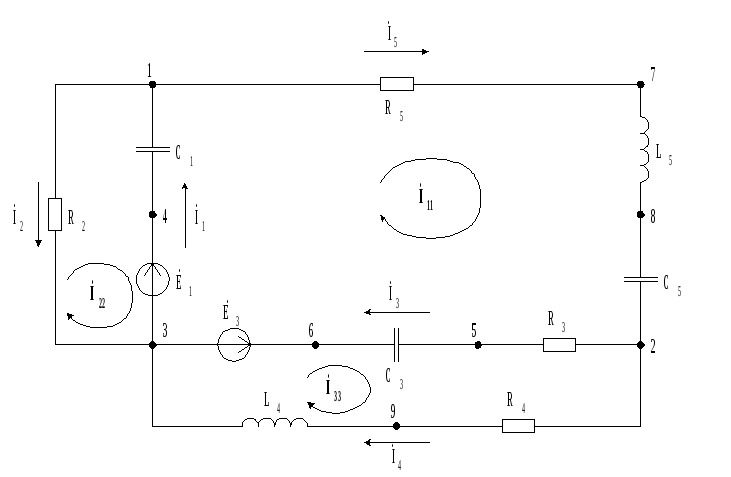
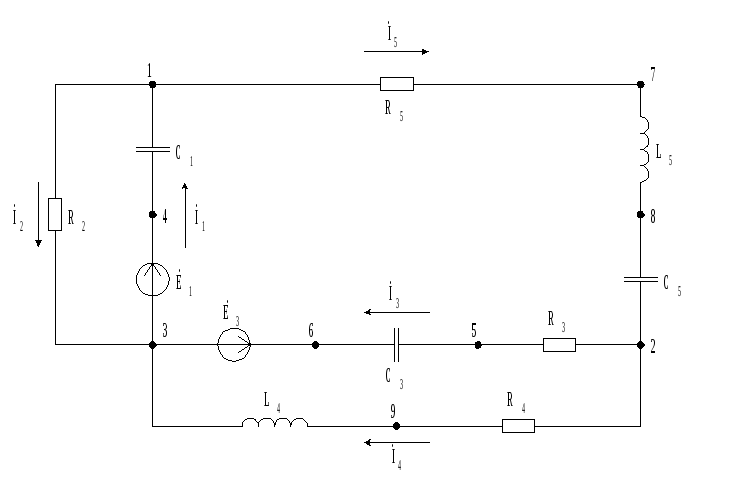
Согласно индивидуальному заданию, составить схему электрической цепи, обозначить все элементы, задать направления токов. В распечатке исходных данных сопротивления даны в омах, индуктивности – в миллигенри, емкости – в микрофарадах, модули комплексов ЭДС – в вольтах, аргументы комплексов ЭЖС – в градусах, частота основной гармоники ЭДС (частота синусоидального ЭДС) – 50 герц.
Составить систему уравнений по законам Кирхгофа в дифференциальной и комплексной форме.
Определить токи в ветвях схемы методом контурных токов.
Записать мгновенные значения токов.
Проверить правильность расчетов по законам Кирхгофа.
Составить баланс активных и реактивных мощностей.
Составить топографическую диаграмму напряжений, совместив ее с векторной диаграммой токов ветвей схемы.
Определить токи в ветвях цепи при введении индуктивной связи между двумя индуктивностями.
Анализ электрической цепи синусоидального тока.
Определить для исходной схемы мгновенные значения токов в ветвях при замене синусоидальных источников напряжений на периодические несинусоидальные.

E1 = E3-4 = 50 310 В = 50*cos310 + j50*sin310 = 32,1394 – j38,3022 В
E3 = E3-6 = 20 320 В = 20*cos320 + j20*sin320 = 15,3209 – j12,8558 В
Система уравнений в дифференциальной форме:
по первому закону Кирхгофа:
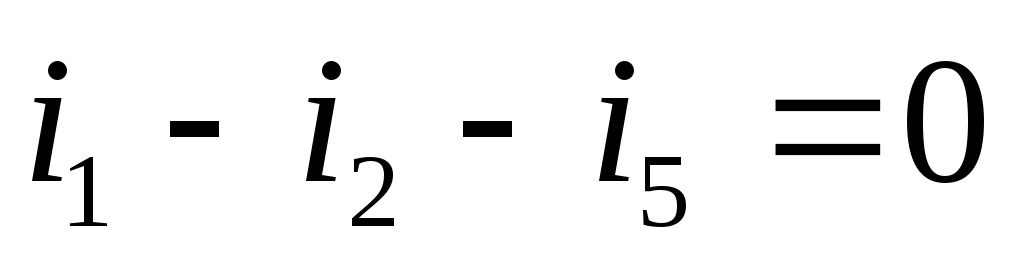
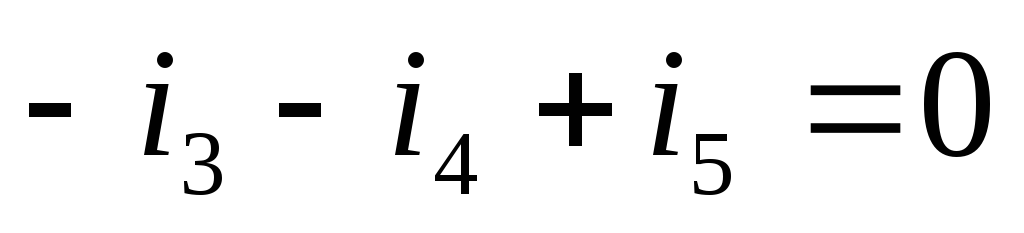
по второму закону Кирхгофа:
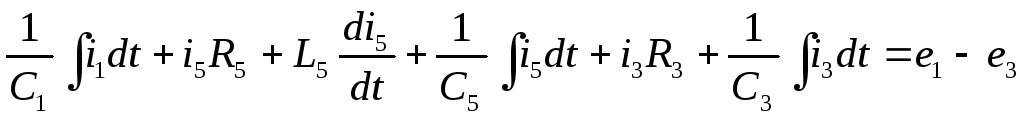
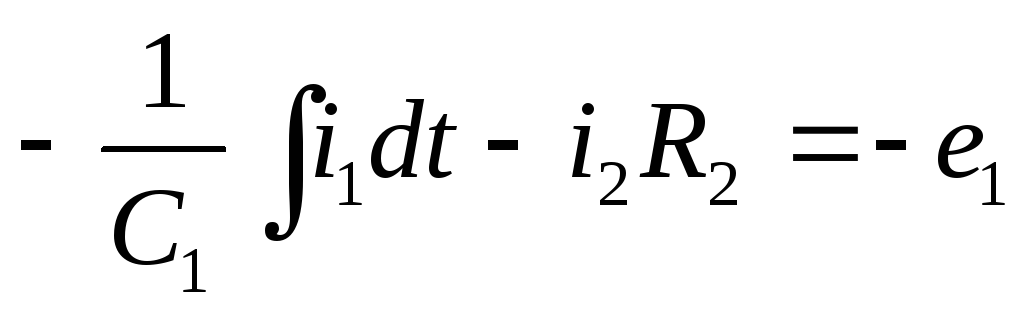

Система уравнений в комплексной форме:
по первому закону Кирхгофа:
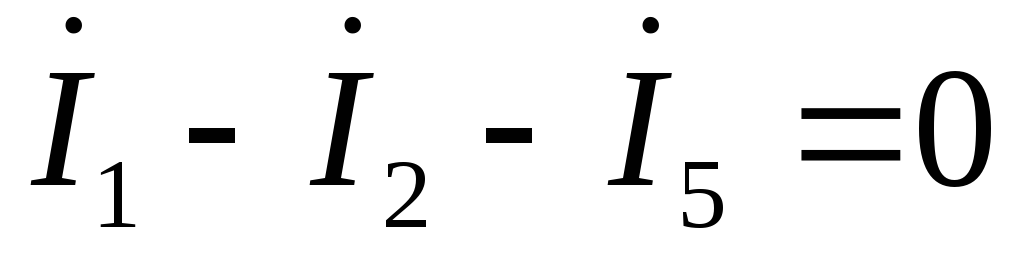

по второму закону Кирхгофа:
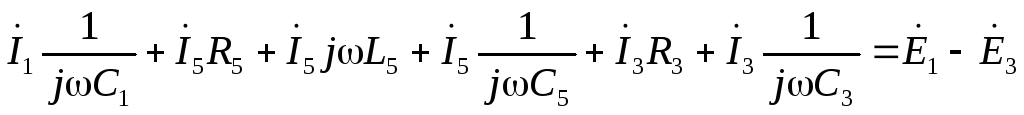
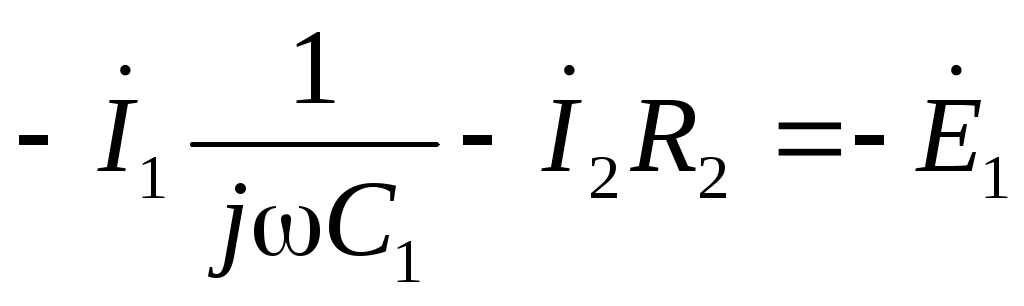
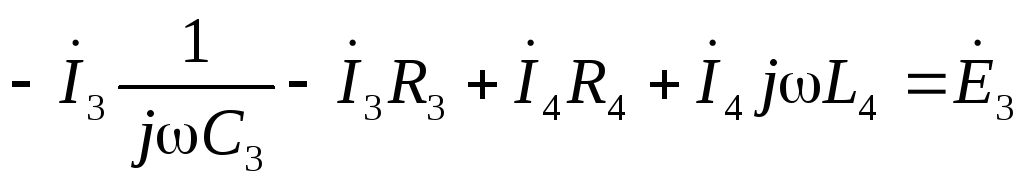
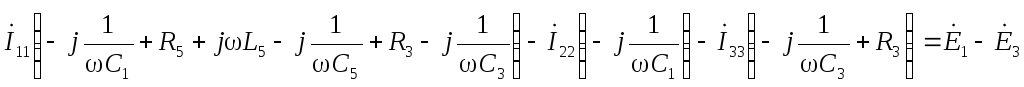
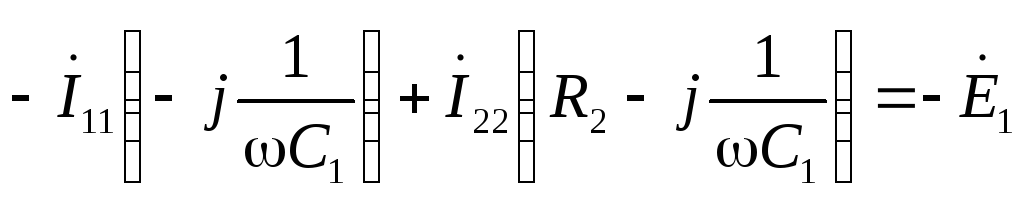
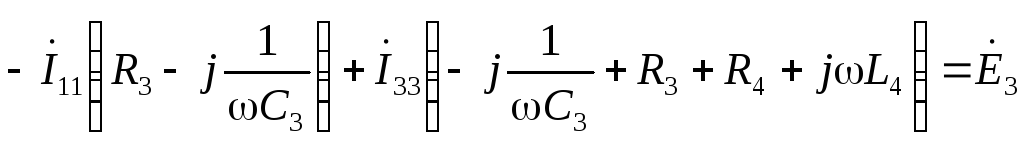
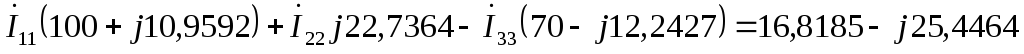
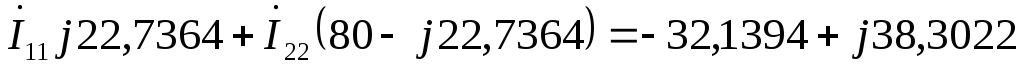

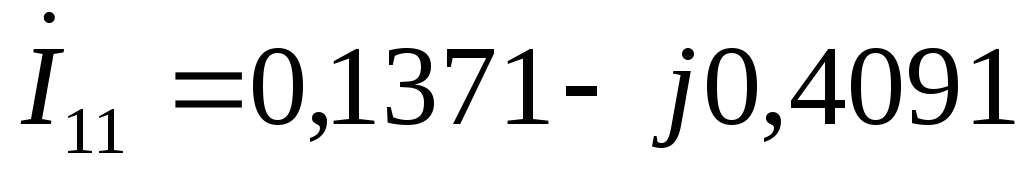 А
А  А
А  А
А
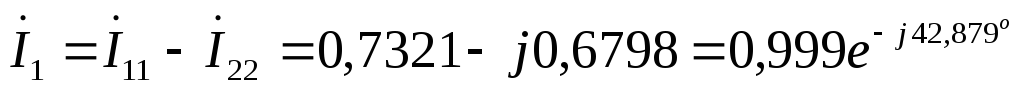 А
А 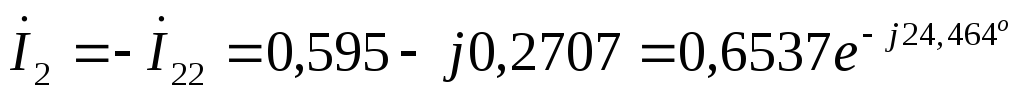 А
А 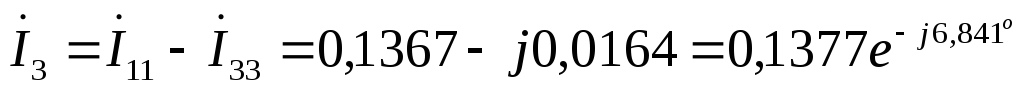 А
А 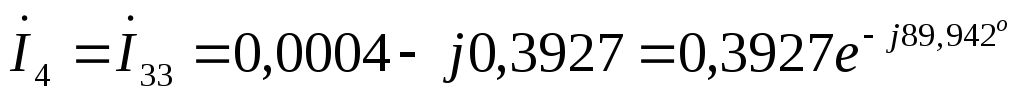 А
А 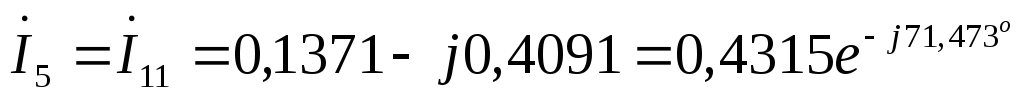 А
А

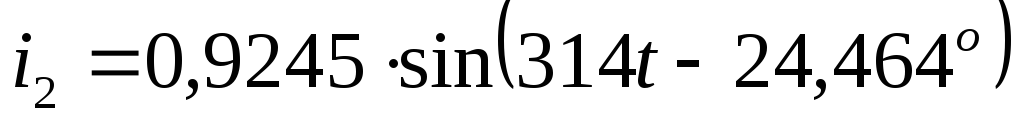

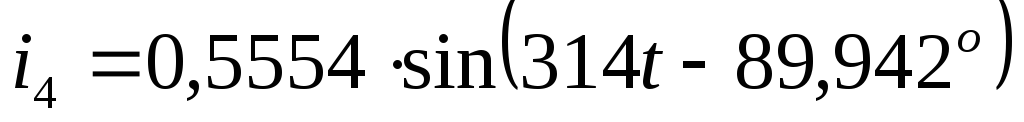
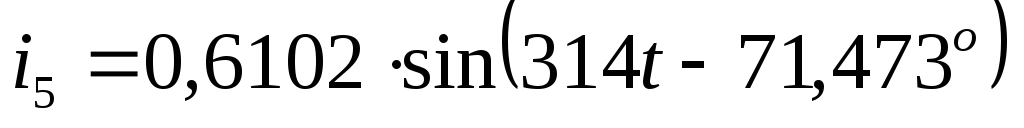
по первому закону Кирхгофа:
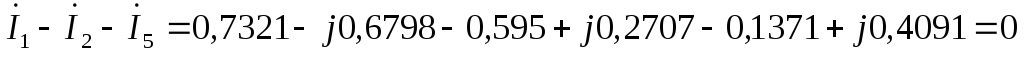
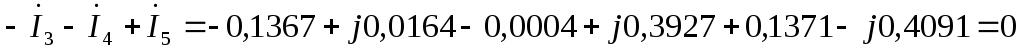
по второму закону Кирхгофа:
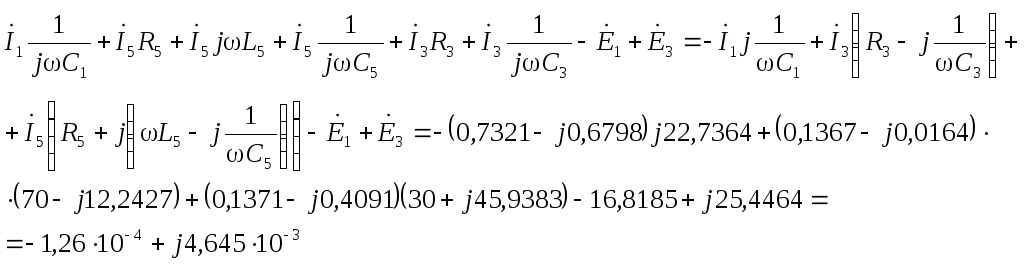

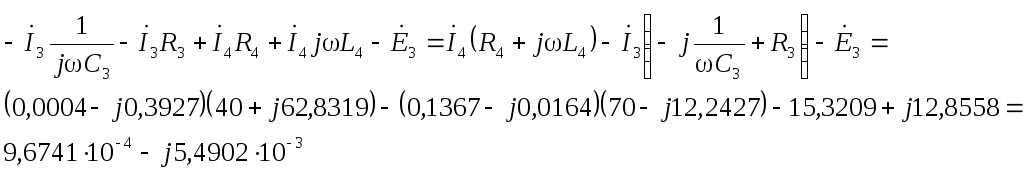
Проверки на законы Кирхгофа показали, что расчеты выполнены верно.
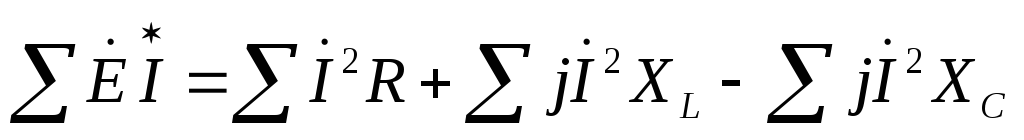
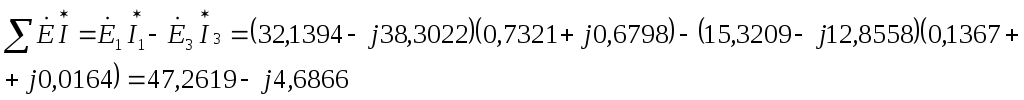
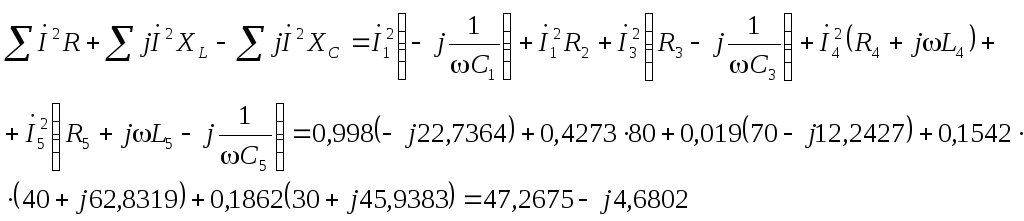

Баланс мощностей сошелся (почти).
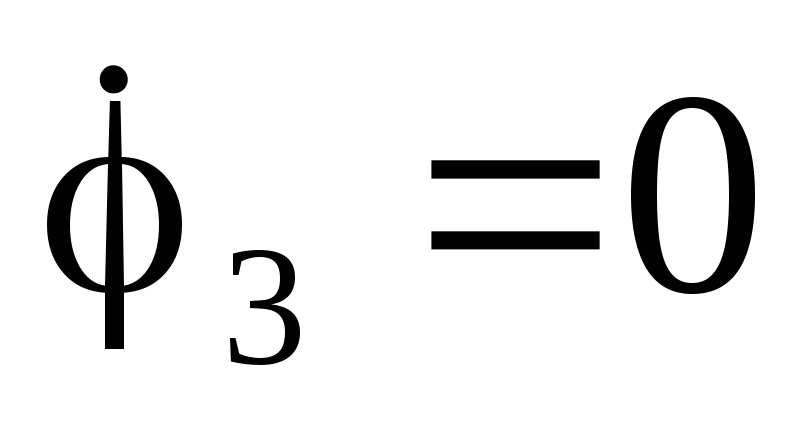 В
В 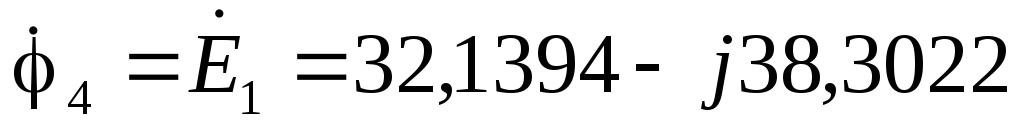 В
В 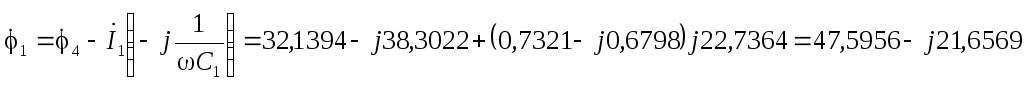
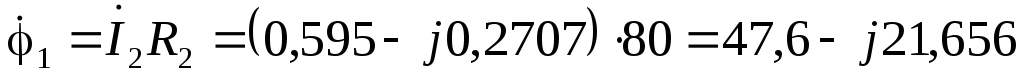 В
В 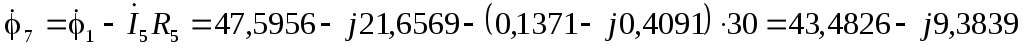 В
В 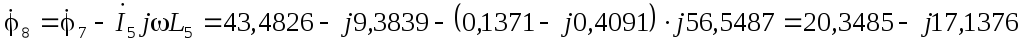 В
В 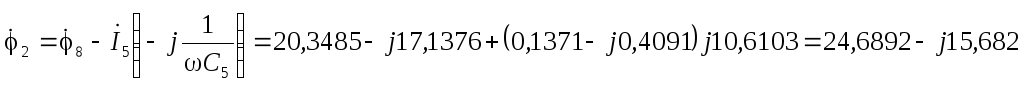 В
В 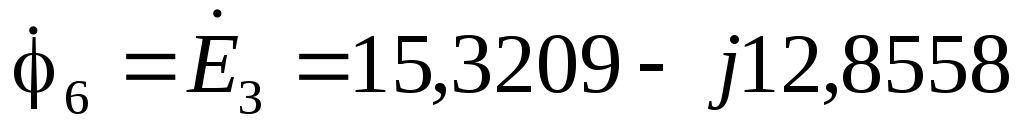 В
В 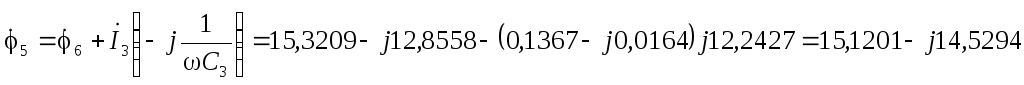 В
В 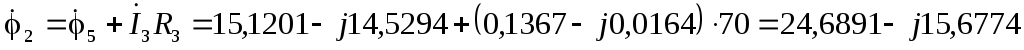 В
В 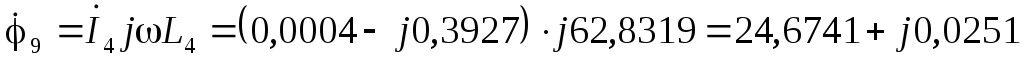 В
В 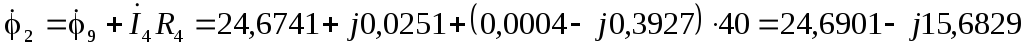 В
В
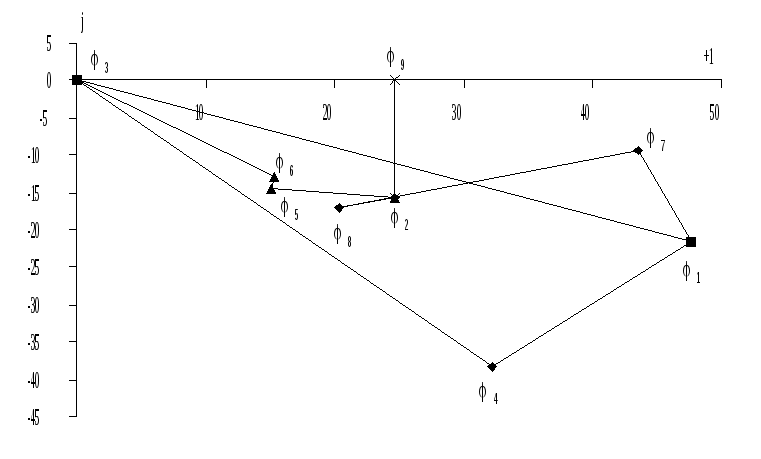
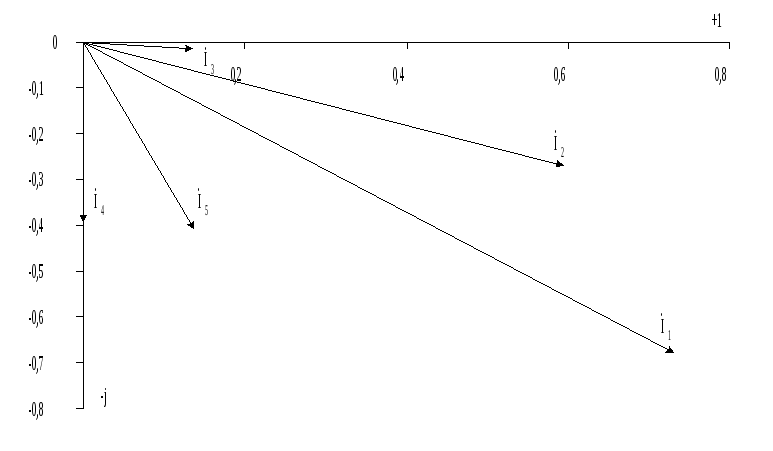

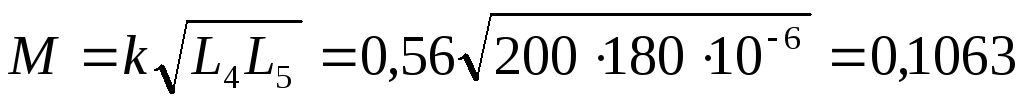
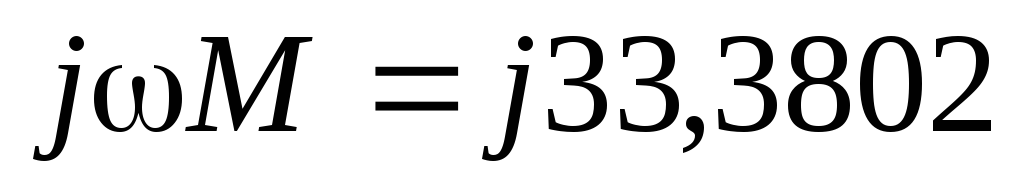

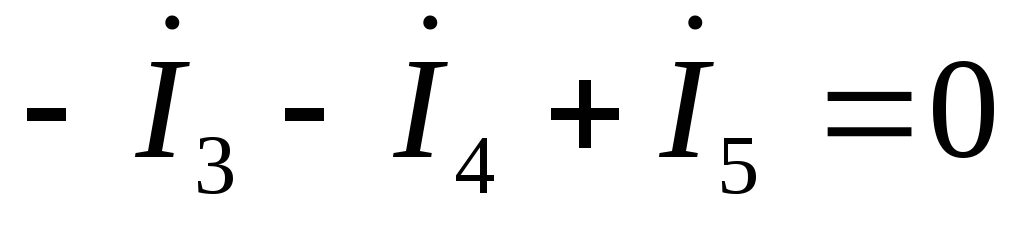
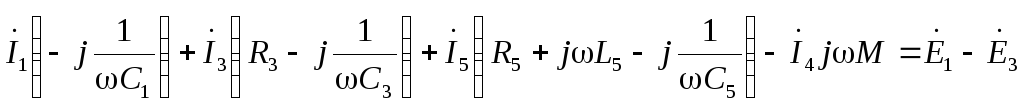
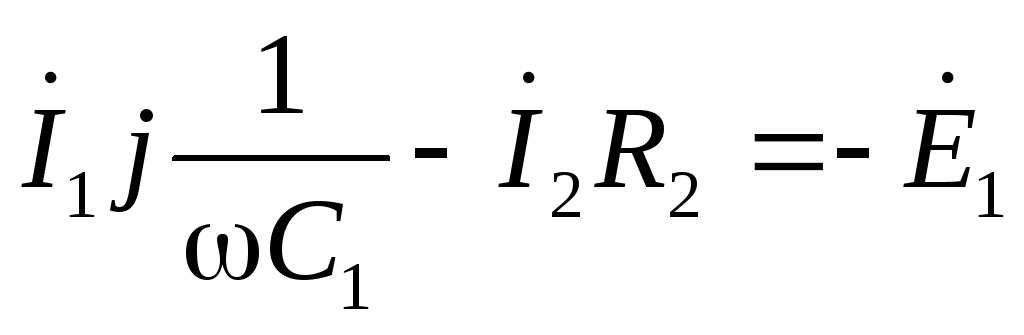
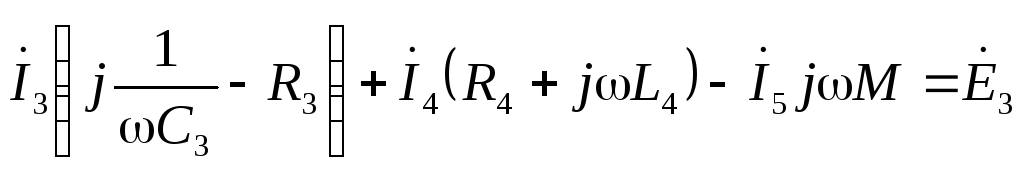
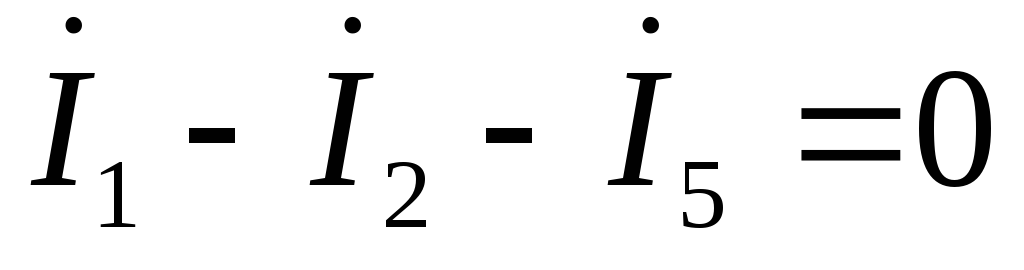
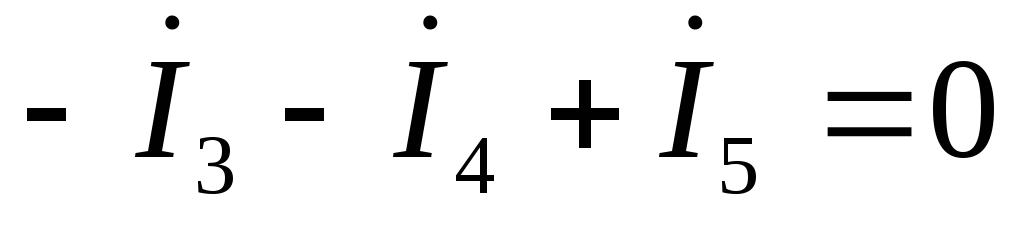
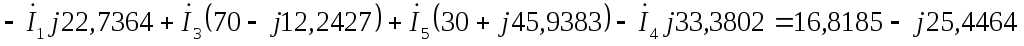
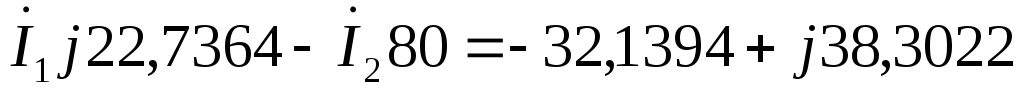
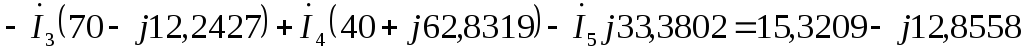
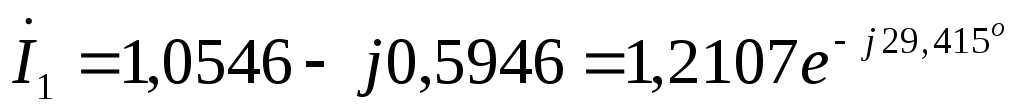 А
А 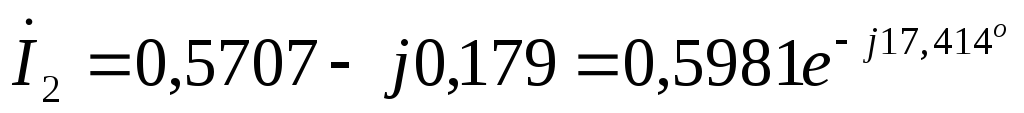 А
А 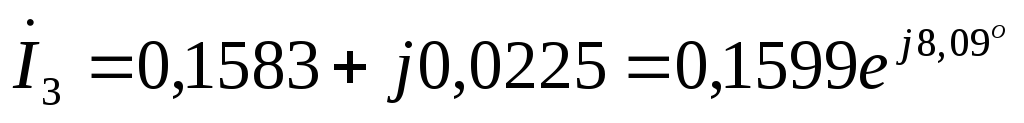 А
А 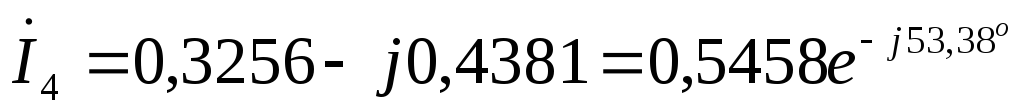 А
А 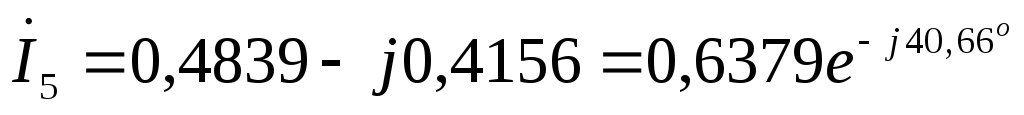 А
А
Нулевая гармоника:
Отсутствует частота, следовательно сопротивления в емкостях равны бесконечности, а в индуктивностях – нулю. Схема принимает вид:
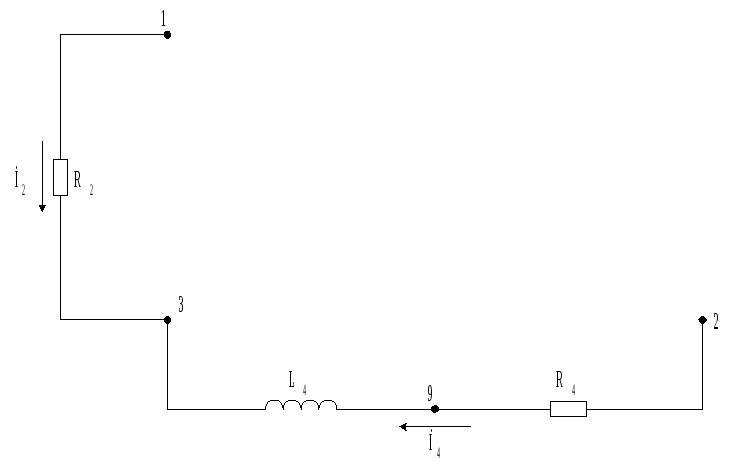
Поскольку не имеется ни одного замкнутого контура, то нулевая гармоника тока не создает.
Первая гармоника:
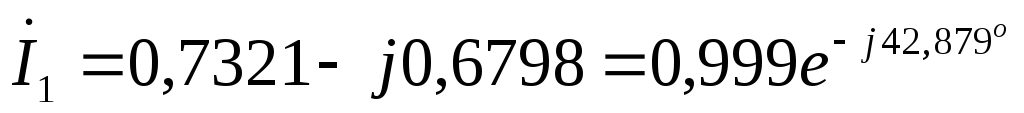 А
А  А
А 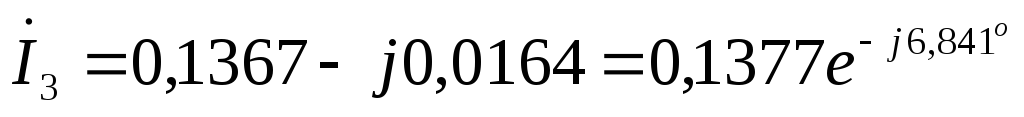 А
А 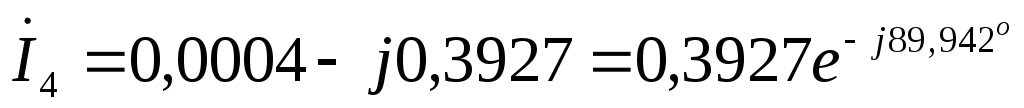 А
А 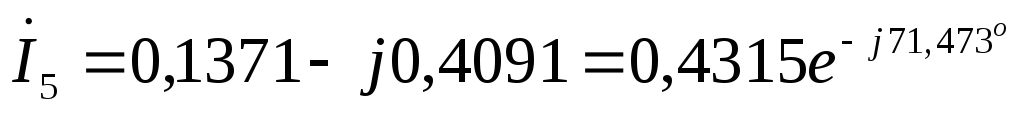 А
А
Третья гармоника:
E1 = E3-4 = 40 70 = 40*cos70 + j40*sin70 = 13,6808 + j37,5877 В
E3 = E3-6 = 10 100 = 10*cos100 + j10*sin100 = –1,7365 + j9,8481 В
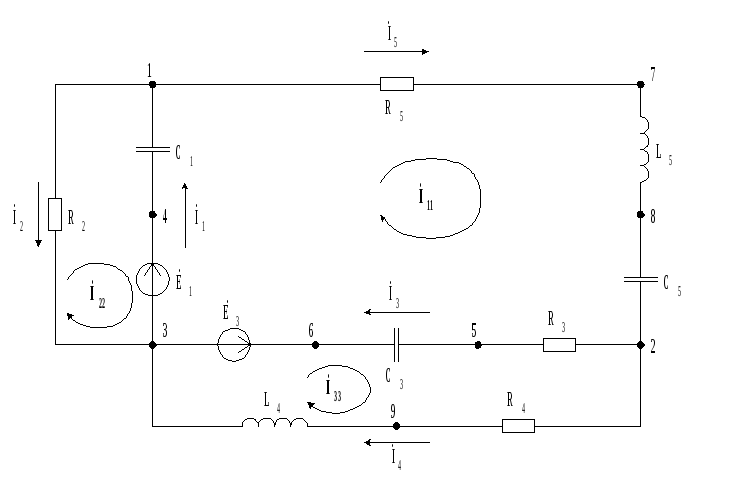
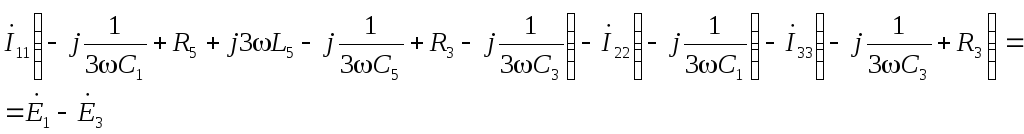
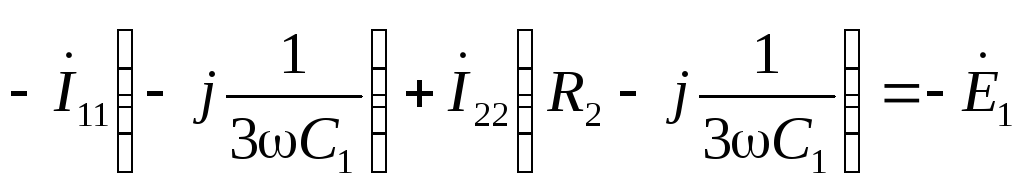
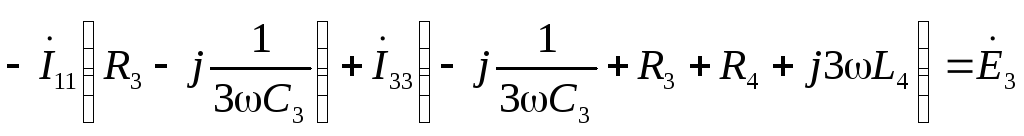

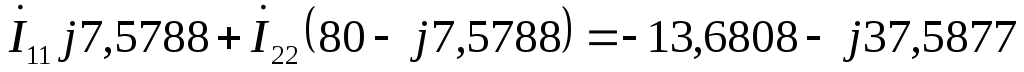
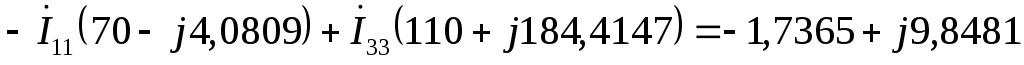
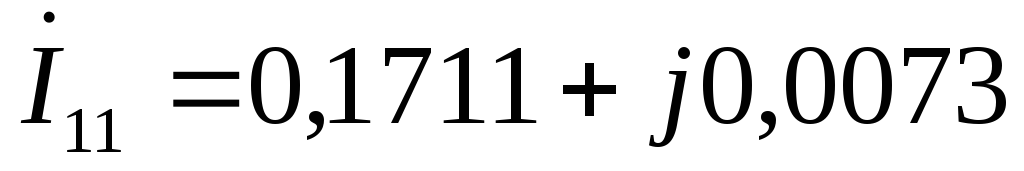 А
А  А
А 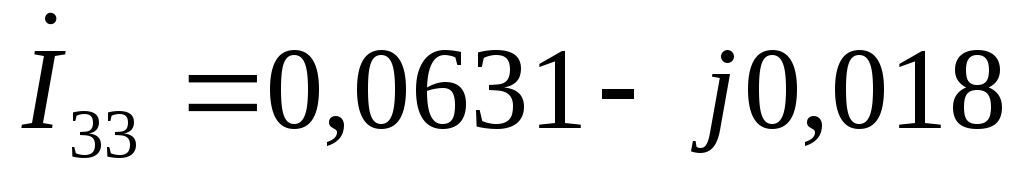 А
А
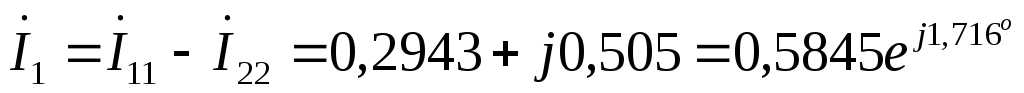 А
А 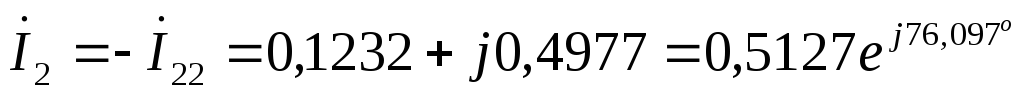 А
А 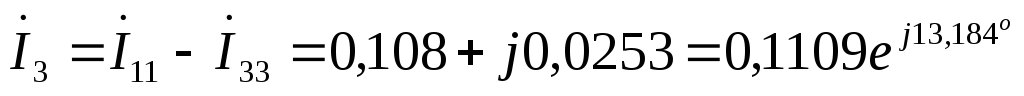 А
А  А
А 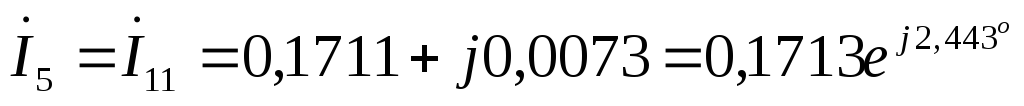 А
А
 А
А  А
А  А
А 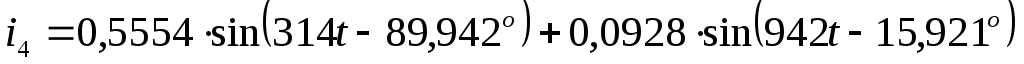 А
А 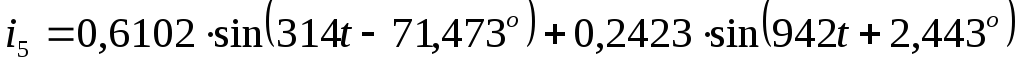 А
А

