Запишите формулу закона ома для участка цепи

Закон Ома для участка цепи – полученный экспериментальным (эмпирическим) путём закон, который устанавливает связь силы тока на участке цепи с напряжением на концах этого участка и его сопротивлением. Строгая формулировка закона Ома для участка цепи записывается так: сила тока в цепи прямо пропорциональна напряжению на её участке и обратно пропорциональна сопротивлению этого участка.

Формула закона Ома для участка цепи записывается в следующем виде:

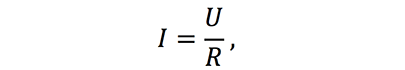
I – сила тока в проводнике [А];

U – электрическое напряжение (разность потенциалов) [В];

R – электрическое сопротивление (или просто сопротивление) проводника [Ом].

Исторически сложилось, что сопротивление R в законе Ома для участка цепи считается основной характеристикой проводника, так как зависит исключительно от параметров этого проводника. Необходимо отметить, что закон Ома в упомянутой форме справедлив для металлов и растворов (расплавов) электролитов и только для тех цепей, где нет реального источника тока или источник тока является идеальным. Идеальный источник тока – это такой источник, который не обладает собственным (внутренним) сопротивлением. Подробнее с законом Ома в применении к цепи с источником тока можно познакомится в нашей статье. Условимся считать положительным направлением слева направо (см. рисунок ниже). Тогда напряжение на участке равно разности потенциалов.

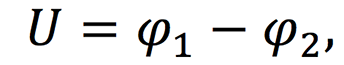
φ₁ – потенциал в точке 1 (в начале участка);

φ₂ – потенциал в точке 2 (а конце участка).

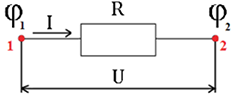
Если выполняется условие φ₁ > φ₂, то напряжение U > 0. Следовательно, линии напряженности в проводнике направлены от точки 1 к точке 2, а значит и ток течет в этом направлении. Именно такое направление тока будем считать положительным I > O.

Рассмотрим простейший пример определения сопротивления на участке цепи с помощью закона Ома. В результате эксперимента с электрической цепью амперметр (прибор, который показывает силу тока) показывает , а вольтметр . Необходимо определить сопротивление участка цепи .

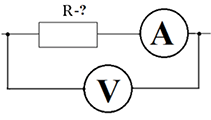
По определению закона Ома для участка цепи

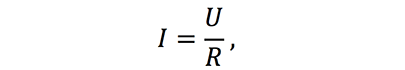
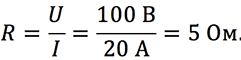
Изучая закон Ома для участка цепи в 8 классе школы, учителя часто задают ученикам следующие вопросы, чтобы закрепить пройденный материал:

Между какими величинами Закон Ома для участка цепи устанавливает зависимость?

– Правильный ответ: между силой тока [I], напряжением [U] и сопротивлением [R].

Отчего кроме напряжения зависит сила тока?

– Правильный ответ: От сопротивления

Как зависит сила тока от напряжения проводника?

– Правильный ответ: Прямо пропорционально

Как зависит сила тока от сопротивления?

– Правильный ответ: обратно пропорционально.

Данные вопросы задают для того, чтобы в 8 классе ученики смогли запомнить закон Ома для участки цепи, определение которого гласит, что сила тока прямо пропорциональна напряжению на концах проводника, если при этом сопротивление проводника не меняется.

Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.

Закон Ома для участка цепи:

Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

1. I — сила тока (в системе СИ измеряется — Ампер)
2. Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
3. Формула: I=frac
4. U — напряжение (в системе СИ измеряется — Вольт)

Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.

Формула: U=IR

R— электрическое сопротивление (в системе СИ измеряется — Ом).

Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.

Формула R=frac

Определение единицы сопротивления — Ом

1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1(Вольт) протекает ток 1 (Ампер).

Закон Ома для полной цепи

Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника

Формула I=frac <varepsilon>

• varepsilon — ЭДС источника напряжения, В;
• I — сила тока в цепи, А;
• R — сопротивление всех внешних элементов цепи, Ом;
• r — внутреннее сопротивление источника напряжения, Ом.

Как запомнить формулы закона Ома

Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.

.

• U — электрическое напряжение;
• I — сила тока;
• P — электрическая мощность;
• R — электрическое сопротивление

Смотри также:

Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.

В данной статье расскажем про закон Ома, формулы для полной цепи (замкнутой), участка цепи, неоднородного участка цепи, в дифференциальной и интегральной форме, переменного тока, а также для магнитной цепи. Вы узнаете какие материалы соответствуют и не соответствуют закону Ома, а также где он встречается.
Закон Ома: постоянный ток , протекающий через проводник, прямо пропорционален напряжению , приложенному к его концам и обратно пропорционален сопротивлению .

Закон Ома был сформулирован немецким физиком и математиком Георгом Омом в 1825-26 годах на основе опыта. Это экспериментальный закон, а не универсальный — он применим к некоторым материалам и условиям.

Закон Ома является частным случаем более позднего и более общего — второго закона Кирхгофа

Ниже будет представлено видео, в котором объясняется закон Ома на пальцах.

Формула закона Ома для участка цепи

Интенсивность постоянного тока, протекающего через проводник, пропорциональна напряжению, приложенному к его концам. В интернете часто называют данную формулу первым законом Ома:

I — сила (интенсивность) тока

Электрическое сопротивление:

Коэффициент пропорциональности R называется электрическим сопротивлением или сопротивлением.

Отношение напряжения к току для данного проводника является постоянным:

Единица электрического сопротивления составляет 1 Ом (1 Ω):

Резистор имеет сопротивление 1, если приложенное напряжение 1 вольт и сила тока составляет 1 ампер.

Зависимость электрического сопротивления от размера направляющей:

Сопротивление проводящей секции с постоянным поперечным сечением R прямо пропорционально длине этого сегмента li, обратно пропорциональному площади поперечного сечения S:

R — электрическое сопротивление

ρ — удельное сопротивление

I — длина направляющей

S — площадь поперечного сечения

Эта зависимость была подтверждена экспериментально британским физиком Хамфри Ди в 1822 году до разработки закона Ома.

Закон Ома для замкнутой (полной) цепи

Закон Ома для полной цепи — это значение силы (интенсивности) тока в настоящей цепи, который зависит от сопротивления нагрузки и от источника тока (E), также его называют вторым законом Ома.

Электрическая лампочка является потребителем источника тока, подключив их вместе, они создают полную электро-цепь. На картинке выше, вы можете увидеть полную электрическую цепь, состоящую из аккумулятора и лампы накаливания.

Электричество, проходит через лампу накаливания и через сам аккумулятор. Следовательно, ток проходя через лампу, в дальнейшем пройдет и через аккумулятор, то есть сопротивление лампочки складывается со сопротивлением аккумулятора.

Сопротивление нагрузки (лампочка), называют внешним сопротивлением, а сопротивление источника тока (аккумулятора) — внутренним сопротивление. Сопротивление аккумулятора обозначается латинской буквой r.

Когда электричество течет вокруг цепи, внутреннее сопротивление самой ячейки сопротивляется потоку тока, и поэтому тепловая энергия теряется в самой ячейке.

• E = электродвижущая сила в вольтах, V
• I = ток в амперах, A
• R = сопротивление нагрузки в цепи в Омах, Ω
• r = внутреннее сопротивление ячейки в Омах, Ω

Мы можем изменить это уравнение;

В этом уравнении появляется ( V ), что является конечной разностью потенциалов, измеренной в вольтах (V). Это разность потенциалов на клеммах ячейки при протекании тока в цепи, она всегда меньше э.д.с. ячейки.

Закон Ома для неоднородного участка цепи

Если на участке цепи действуют только потенциальные силы (Рисунок 1а), то закон Ома записывается в известном виде . Если же в кругу проявляется еще и действие сторонних сил (Рисунок 2б), то закон Ома примет вид , откуда . Это и есть закон Ома для любого участка цепи.

Закон Ома можно распространить и на весь круг. Соединив точки 2 и 1 (Рисунок 3в), преобразуем разность потенциалов в ноль, и учитывая сопротивление источника тока, закон Ома примет вид . Это и есть выражение закона Ома для полной цепи.

Последнее выражение можно представить в различных формах. Как известно, напряжение на внешнем участке зависит от нагрузки, то есть или , или .

В этих выражениях Ir — это падение напряжения внутри источника тока, а также видно, что напряжение U меньше ε на величину Ir . Причем, чем больше внешнее сопротивление по сравнению с внутренним, тем больше U приближается к ε.

Рассмотрим два особых случая, в отношении внешнего сопротивления цепи.

1) R = 0 — такое явление называют коротким замыканием. Тогда, из закона Ома имеем — , то есть ток в цепи возрастает до максимума, а внешний спад напряжения U → 0. При этом в источнике выделяется большая мощность, что может привести к его неисправности.

2) R = ∞ , то есть электрическая цепь разорвана, тогда , а . Итак, в этом случае, ЭДС численно равна напряжению на клеммах разомкнутого источника тока.

Закон Ома в дифференциальной форме

Закон Ома можно представить в таком виде, чтобы он не был связан с размерами проводника. Выделим участок проводника Δ l , на концах которой приложено потенциалы φ ₁ и φ ₂. Когда средняя площадь сечения проводника Δ S , а плотность тока j , то сила тока

Если Δ l → 0, то взяв предел отношения, . Итак, окончательно получим , или в векторной форме — это выражение закона Ома в дифференциальной форме. Этот закон выражает силу тока в произвольной точке проводника в зависимости от его свойств и электрического состояния.

Закон ома для переменного тока

Это уравнение представляет собой запись закона Ома для цепей переменного тока относительно их амплитудных значений. Понятно, что оно будет справедливым и для эффективных значений силы и тока: .

Для цепей переменного тока возможен случай, когда , а это значит, что U _L = U _C . Поскольку эти напряжения находятся в противофазе, то они компенсируют друг друга. Такие условия называют резонансом напряжений. Резонанс можно достичь или при ω = const , изменяя С и L , или же при постоянных С и L подбирают ω, которая называется резонансным. Как видно — .

Особенности резонанса напряжений следующие:

• полное сопротивление цепи минимальное, Z=R ;
• амплитуда тока — максимальная ;
• амплитуда значений приложенного напряжения равна амплитуде на активном сопротивлении;
• напряжение и ток находятся в одинаковых фазах (φ = 0);
• мощность источника передается только активному сопротивлению, следовательно полезная мощность — максимальная.

Резонанс токов получают при параллельном соединении индуктивности и емкости на рисунке слева. По первому закону Кирхгофа результирующий ток в какой-то момент времени I = IL+IC. Несмотря на то, что суммы ІL и IC могут быть достаточно большими, ток в главном круге станет равным нулю, а значит сопротивление цепи станет максимальным.
Зависимость силы тока от частоты при различных активных сопротивлениях показана на рисунке справа.

Закон Ома в интегральной форме

С дифференциального закона Ома можно непосредственно получить интегральный закон. Для этого умножим скалярно левую и правую части выражения на элементарную длину проводника (перемещение носителя тока), образовав соотношение

В (1) j*S _n = И есть величина силы тока. Проинтегрируем (1) по участку круга L с точки 1 до точки 2

есть сопротивление проводника, а — удельное сопротивление. Интеграл в правой части (2) является напряжение U на концах участка

Окончательно из (2) — (4) имеем выражение для закона Ома в интегральной форме

который он установил экспериментально.

Интерпретация закона Ома

Интенсивность тока, являющаяся действием приложенного напряжения, ведет себя пропорционально его напряжению. Например: если приложенное напряжение увеличивается в два раза, оно также удваивает силу тока (интенсивность тока).

Помните, что закон Ома удовлетворяется только частью материалов — в основном металлами и керамическими материалами.

Когда закон Ома встречается и какие материалы соответствуют и не соответствуют закону Ома

Закон Ома является экспериментальным законом, выполненным для некоторых материалов (например, металлов) для фиксированных условий тока, в частности температуры проводника.

Материалы, относящиеся к закону Ома, называются омическими направляющими или линейными проводниками. Примерами проводников, которые соответствуют закону Ома, являются металлы (например, медь, золото, железо), некоторые керамические изделия и электролиты.

Материалы, не относящиеся к закону Ома, в которых сопротивление является функцией интенсивности протекающего через них тока, называются нелинейными проводниками. Примерами руководств, не относящихся к закону Ома, являются полупроводники и газы.

Закон Ома не выполняется, когда изменяются параметры проводника, особенно температура.

Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ