Зарядка конденсатора от источника постоянного напряжения

Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление.

Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление. Формулы, по которым идет расчет, приведены под калькуляторами.

Заряд конденсатора от источника постоянной ЭДС

Разряд конденсатора через сопротивление

Понять приводимые ниже формулы поможет картинка, изображающая электрическую схему заряда конденсатора от источника постоянной ЭДС (батареи):

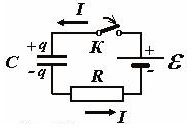
Итак, при замыкании ключа К в цепи пойдет электрический ток, который будет приводить к заряду конденсатора.
По закону Ома сумма напряжений на конденсаторе и резисторе равна ЭДС источника, таким образом:

При этом заряд и сила тока зависят от времени. В начальный момент времени на конденсаторе нет заряда, сила тока максимальна, также как и максимальна мощность, рассеиваемая на резисторе.

Во время зарядки конденсатора, напряжение на нем изменяется по закону

где величину

называют постоянной времени RC-цепи или временем зарядки конденсатора.
Вообще говоря, согласно уравнению выше, заряд конденсатора бесконечно долго стремится к величине ЭДС, поэтому для оценки времени заряда конденсатора используют величину
— это время, за которое напряжение на конденсаторе достигнет значения 99,2% ЭДС.
Заряд на конденсаторе:

Энергия, запасенная в конденсаторе:

Работа, выполненная источником ЭДС:

Рассмотренный в предыдущем разделе процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теор етический интерес, как метод расчета энерги и конденсатора. Реально конденсаторы заряжают, подключая их к источнику ЭДС, например, к гальванической батарее.

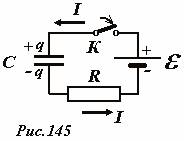
Пусть конденсатор емкостью C подключен к источнику, ЭДС которого равна e (Рис. 145). Полное электрическое сопротивление цепи (включающее и внутренне сопротивление источника) обо значим R . При замыкании ключа в цепи пойдет электрический ток, благодаря которому на обкладках конденсатора будет накапливаться электрический заряд. По закону Ома сумма напряжений на конденсаторе 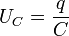и резисторе U R = I R равна ЭДС источника 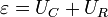, что приводит к уравнению

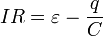. (1)

В этом уравнении заряд конденсатора и сила тока зависят от времени. Скорость изменения заряда конденсатора по определению равна силе тока в цепи 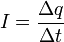, что позволяет получить уравнение, описывающее изменение заряда конденсатора с течением времени

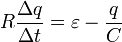. (2)

Можно также получить уравнение, непосредственно описывающее изменение силы тока в цепи с течением времени. Для этого на основании уравнения (1) запишем уравнения для малых изменений входящих величин

.

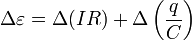Формально эту операцию можно описать следующим образом: уравнение (1) следует записать для двух моментов времени t и ( t + Delta t ), а затем из второго уравнения вычесть первое. Так как ЭДС источника постоянна, то ее изменение равно нулю Delta e = 0, сопротивление цепи и емкость конденсатора постоянны, поэтому их можно вынести из под знака изменения Delta, поэтому полученное уравнение приобретает вид

.

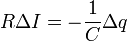Наконец разделим его на промежуток времени, в течение которого произошли эти изменения, в результате получаем искомое уравнение (с учетом связи между силой тока и изменения заряда)

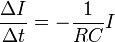. (3)

Математический смысл этого уравнения указывает, что скорость уменьшения тока пропорциональна самой силе тока. Для однозначного решения этого уравнения необходимо задать начальное условие – значение силы тока в начальный момент времени I 0 = I(0).

С уравнениями такого типа мы познакомились в «математическом отступлении» , поэтому здесь его анализ проведем кратко. В начальный момент времени, когда заряд конденсатора равен нулю, скорость возрастания заряда (то есть сила тока) максимальна и равна 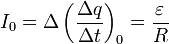. Затем по мере накопления заряда сила тока будет уменьшаться, когда напряжение на конденсаторе станет равным ЭДС источника, заряд конденсатора достигнет максимального стационарного значения 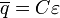и ток в цепи прекратится.

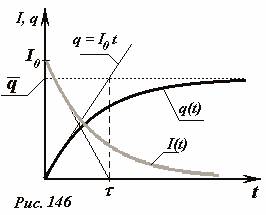
Схематически зависимости заряда конденсатора и силы тока в цепи от времени показаны на рис. 146. Для оценки времени зарядки конденсатора можно принять, что заряд возрастает до максимального значения с постоянной скоростью, равной силе тока в начальный момент времени. В этом случае

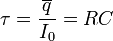. (4)

Аналогичная оценка исчезновения тока, полученная на основании уравнения (3) приводит к этому же результату.

Строго говоря, время зарядки конденсатора, описываемой уравнением (2) равно бесконечности. Это парадокс можно исключить, если принять во внимание дискретность электрического заряда. Кроме того, заряд конденсатора, подключенного к батарее с течением времени случайным образом изменяется, флуктуирует, поэтому рассматриваемое уравнение описывает некоторые усредненные характеристики процесса. Тем не менее, полученная оценка времени RC широко применяется в приближенных расчетах, часто ее называют просто временем зарядки конденсатора .

Рассмотрим теперь превращения различных форм энерги и в данном процессе. Понятно, что причиной тока в цепи и как следствие зарядки конденсатора являются сторонние силы источника. На первый взгляд, энергетический баланс включает определенное противоречие: если источник сообщил конденсатору заряд q , то сторонние силы совершили при этом работу A 0 = q e , при этом энерги я конденсатора стала равной 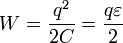, что в два раза меньше работы совершенной источником. Противоречие исчезает, если принять во внимание, что в процессе зарядки по цепи течет электрический ток, поэтому на резисторе выделяется некоторое количество теплоты, то есть часть энерги и источника переходит в тепловую. Мысленно разобьем время зарядки на малые промежутки Delta t i ( i = 1,2,3. ). Перепишем уравнение (1) в виде

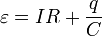, (5)

и умножим его на величину малой порции заряда, переносимого за малый промежуток времени Delta t i , Delta q i = I i Delta t i . В результате получим

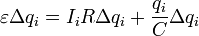. (6)

Здесь обозначено q i – заряд конденсатора перед перенесением рассматриваемой порции заряда. Каждый член полученного уравнения имеет явный физический смысл :

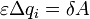– работа сторонних сил по перемещению порции заряда ? q i ; 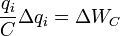– увеличение энерги и конденсатора при увеличении его заряда на Delta q i ; 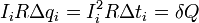– количество теплоты, выделившееся на резисторе, при протекании

порции заряда Delta q i .

Таким образом, закон сохранения энерги и, выражаемый уравнением баланса (6) для малого промежутка времени оказывается выполненным, следовательно, он будет выполнен и для всего процесса зарядки. Просуммируем выражение (5) по всем промежуткам времени зарядки, в результате чего получим:

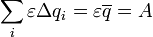– полная работа сторонних сил по перенесению электрического заряда, равного стационарному заряду конденсатора; 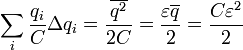– энерги я заряженного конденсатора; наконец, 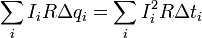– количество выделившейся на резисторе теплоты.

Принимая во внимание уравнение (3) и формулы из «математического отступления» , последнюю сумму можно выразить в виде

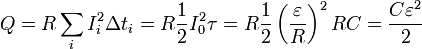. (6)

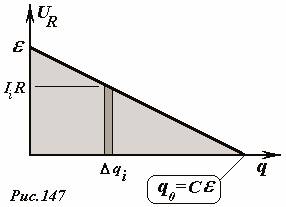
Эта сумма же может быть вычислена графически. Формула (1) задает зависимость напряжения на резисторе U R = I R от заряда конденсатора. Эта зависимость линейна, ее график (Рис. 147) является отрезком прямой линии. За малый промежуток времени через резистор протечет малый заряд Delta q i , при этом выделится количество теплоты 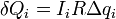, которое численно равно площади узкой полоски, выделенной на рисунке. Полное количество теплоты, выделившейся при прохождении всего заряда численно равно площади треугольника под графиком зависимости U R ( q ), то есть

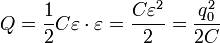. (7)

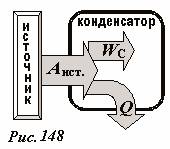
Таким образом, энергетический баланс полностью сходится и для всего процесса целиком: работа, совершенная источником равна сумме энерги и конденсатора и количества выделившейся теплоты A = W C + Q . Схематически преобразование энерги и в этом процессе показано на рис. 148.

Интересно заметить, что количество теплоты, выделяющееся при зарядке, не зависит о сопротивления цепи и в точности равно энерги и конденсатора. То есть, половина энерги и источника переходит в энерги ю электрического поля, а вторая в тепловую энерги ю, выделяющуюся в цепи: природа требует своеобразный пятидесятипроцентный налог в виде тепловых потерь, не зависимо от сопротивления цепи и емкости конденсатора [1] .

Примечания

1. ^ Но эти параметры цепи определяют время процесса.

Об авторе:
Этот материал взят из источника в свободном доступе интернета. Вся грамматика источника сохранена.

Присоединим цепь, состоящую из незаряженного конденсатора емкостью С и резистора с сопротивлением R, к источнику питания с постоянным напряжением U (рис. 16-4).

Так как в момент включения конденсатор еще не заряжен, то напряжение на нем Поэтому в цепи в начальный момент времени падение напряжения на сопротивлении R равно U и возникает ток, сила которого

Рис. 16-4. Зарядка конденсатора.

Прохождение тока i сопровождается постепенным накоплением заряда Q на конденсаторе, на нем появляется напряжение и падение напряжения на сопротивлении R уменьшается:

как и следует из второго закона Кирхгофа. Следовательно, сила тока

уменьшается, уменьшается и скорость накопления заряда Q, так как ток в цепи

С течением времени конденсатор продолжает заряжаться, но заряд Q и напряжение на нем растут все медленнее (рис. 16-5), а сила тока в цепи постепенно уменьшается пропорционально разности – напряжений

Рис. 16-5. График изменения тока и напряжения при зарядке конденсатора.

Через достаточно большой интервал времени (теоретически бесконечно большой) напряжение на конденсаторе достигает величины, равной напряжению источника питания, а ток становится равным нулю — процесс зарядки конденсатора заканчивается.

Практически принято считать, что процесс зарядки закончился, когда ток уменьшился до 1% — начального значения или, – что то же, когда напряжение на конденсаторе достигло 99% напряжения источника питания

Процесс зарядки конденсатора тем продолжительней, чем больше сопротивление цепи R, ограничивающее силу тока, и чем больше емкость конденсатора С, так как при большой емкости должен накопиться больший заряд. Скорость протекания процесса характеризуют постоянной времени цепи

чем больше , тем медленнее процесс.

Постоянная времени цепи имеет размерность времени, так как

Через интервал времени с момента включения цепи, равный , напряжение на конденсаторе достигает примерно 63% напряжения источника питания, а через интервал процесс зарядки конденсатора можно считать закончившимся.

Напряжение на конденсаторе при зарядке

т. е. оно равно разности постоянного напряжения источника питания и свободного напряжения убывающего с течением времени по закону показательной функции от значения U до нуля (рис. 16-5).

Зарядный ток конденсатора

Ток от начального значения постепенно уменьшается по закону показательной функции (рис. 16-5).

б) Разряд конденсатора

Рассмотрим теперь процесс разряда конденсатора С, который был заряжен от источника питания до напряжения U через резистор с сопротивлением R (рис. 16-6, Где переключатель переводится из положения 1 в положение 2).

Рис. 16-6. Разряд конденсатора на резистор.

Рис. 16-7. График изменения тока и напряжения при разрядке конденсатора.

В начальный момент, в цепи возникнет ток и конденсатор начнет разряжаться, а напряжение на нем уменьшаться. По мере уменьшения напряжения будет уменьшаться и ток в цепи (рис. 16-7). Через интервал времени напряжение на конденсаторе и ток цепи уменьшатся при мерно до 1% начальных значений и процесс разряда конденсатора можно считать закончившимся.

Напряжение на конденсаторе при разряде

т. е. уменьшается по закону показательной функции (рис. 16-7).

Разрядный ток конденсатора

т. е. он, так же как и напряжение, уменьшается по тому же закону (рис. 6-7).

Вся энергия, запасенная при зарядке конденсатора в его электрическом поле, при разряде выделяется в виде тепла в сопротивлении R.

Электрическое поле заряженного конденсатора, отсоединенного от источника питания, не может долго сохраняться неизменным, так как диэлектрик конденсатора и изоляция между его зажимами обладают некоторой проводимостью.

Разряд конденсатора, обусловленный несовершенством диэлектрика и изоляции, называется саморазрядом. Постоянная времени при саморазряде конденсатора не зависит от формы обкладок и расстояния между ними.

Процессы зарядки и разряда конденсатора называются переходными процессами.