Присоединим цепь, состоящую из незаряженного конденсатора емкостью С и резистора с сопротивлением R, к источнику питания с постоянным напряжением U (рис. 16-4).
Так как в момент включения конденсатор еще не заряжен, то напряжение на нем 
Поэтому в цепи в начальный момент времени 
падение напряжения на сопротивлении R равно U и возникает ток, сила которого
Рис. 16-4. Зарядка конденсатора.
Прохождение тока i сопровождается постепенным накоплением заряда Q на конденсаторе, на нем появляется напряжение 
и падение напряжения на сопротивлении R уменьшается:
как и следует из второго закона Кирхгофа. Следовательно, сила тока
уменьшается, уменьшается и скорость накопления заряда Q, так как ток в цепи
С течением времени конденсатор продолжает заряжаться, но заряд Q и напряжение на нем 
растут все медленнее (рис. 16-5), а сила тока в цепи постепенно уменьшается пропорционально разности – напряжений 
Рис. 16-5. График изменения тока и напряжения при зарядке конденсатора.
Через достаточно большой интервал времени (теоретически бесконечно большой) напряжение на конденсаторе достигает величины, равной напряжению источника питания, а ток становится равным нулю — процесс зарядки конденсатора заканчивается.
Практически принято считать, что процесс зарядки закончился, когда ток уменьшился до 1% — начального значения 
или, – что то же, когда напряжение на конденсаторе достигло 99% напряжения источника питания 
Процесс зарядки конденсатора тем продолжительней, чем больше сопротивление цепи R, ограничивающее силу тока, и чем больше емкость конденсатора С, так как при большой емкости должен накопиться больший заряд. Скорость протекания процесса характеризуют постоянной времени цепи
чем больше 
, тем медленнее процесс.
Постоянная времени цепи имеет размерность времени, так как
Через интервал времени с момента включения цепи, равный 
, напряжение на конденсаторе достигает примерно 63% напряжения источника питания, а через интервал 
процесс зарядки конденсатора можно считать закончившимся.
Напряжение на конденсаторе при зарядке
т. е. оно равно разности постоянного напряжения источника питания и свободного напряжения 
убывающего с течением времени по закону показательной функции от значения U до нуля (рис. 16-5).
Зарядный ток конденсатора
Ток 
от начального значения 
постепенно уменьшается по закону показательной функции (рис. 16-5).
б) Разряд конденсатора
Рассмотрим теперь процесс разряда конденсатора С, который был заряжен от источника питания до напряжения U через резистор с сопротивлением R (рис. 16-6, Где переключатель переводится из положения 1 в положение 2).
Рис. 16-6. Разряд конденсатора на резистор.
Рис. 16-7. График изменения тока и напряжения при разрядке конденсатора.
В начальный момент, в цепи возникнет ток 
и конденсатор начнет разряжаться, а напряжение на нем уменьшаться. По мере уменьшения напряжения 
будет уменьшаться и ток в цепи 
(рис. 16-7). Через интервал времени 
напряжение на конденсаторе и ток цепи уменьшатся при мерно до 1% начальных значений и процесс разряда конденсатора можно считать закончившимся.
Напряжение на конденсаторе при разряде
т. е. уменьшается по закону показательной функции (рис. 16-7).
Разрядный ток конденсатора
т. е. он, так же как и напряжение, уменьшается по тому же закону (рис. 6-7).
Вся энергия, запасенная при зарядке конденсатора в его электрическом поле, при разряде выделяется в виде тепла в сопротивлении R.
Электрическое поле заряженного конденсатора, отсоединенного от источника питания, не может долго сохраняться неизменным, так как диэлектрик конденсатора и изоляция между его зажимами обладают некоторой проводимостью.
Разряд конденсатора, обусловленный несовершенством диэлектрика и изоляции, называется саморазрядом. Постоянная времени при саморазряде конденсатора 
не зависит от формы обкладок и расстояния между ними.
Процессы зарядки и разряда конденсатора называются переходными процессами.
Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление.
Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление. Формулы, по которым идет расчет, приведены под калькуляторами.
Заряд конденсатора от источника постоянной ЭДС
Разряд конденсатора через сопротивление
Понять приводимые ниже формулы поможет картинка, изображающая электрическую схему заряда конденсатора от источника постоянной ЭДС (батареи):
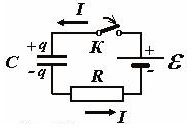
Итак, при замыкании ключа К в цепи пойдет электрический ток, который будет приводить к заряду конденсатора.
По закону Ома сумма напряжений на конденсаторе и резисторе равна ЭДС источника, таким образом:
При этом заряд и сила тока зависят от времени. В начальный момент времени на конденсаторе нет заряда, сила тока максимальна, также как и максимальна мощность, рассеиваемая на резисторе.
Во время зарядки конденсатора, напряжение на нем изменяется по закону
где величину
называют постоянной времени RC-цепи или временем зарядки конденсатора.
Вообще говоря, согласно уравнению выше, заряд конденсатора бесконечно долго стремится к величине ЭДС, поэтому для оценки времени заряда конденсатора используют величину
— это время, за которое напряжение на конденсаторе достигнет значения 99,2% ЭДС.
Заряд на конденсаторе:
Энергия, запасенная в конденсаторе:
Работа, выполненная источником ЭДС:
Для того чтобы зарядить конденсатор, необходимо включить его в цепь постоянного тока. На рис. 1 показана схема заряда конденсатора. Конденсатор С присоединен к зажимам генератора. При помощи ключа можно замкнуть или разомкнуть цепь. Рассмотрим подробно процесс заряда конденсатора.
Генератор обладает внутренним сопротивлением. При замыкании ключа конденсатор зарядится до напряжения между обкладками, равного э. д. с. генератора: Uс = Е. При этом обкладка, соединенная с положительным зажимом генератора, получает положительный заряд (+ q ), а вторая обкладка получает равный по величине отрицательный заряд ( -q ). Величина заряда q прямо пропорциональна емкости конденсатора С и напряжению на его обкладках: q = CUc
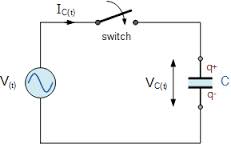
P ис. 1 . Схема заряда конденсатора
Для того чтобы обкладки конденсатора зарядились, необходимо, чтобы одна из них приобрела, а другая потеряла некоторое количество электронов. Перенос электронов от одной обкладки к другой совершается по внешней цепи электродвижущей силой генератора, а сам процесс перемещения зарядов по цепи есть не что иное, как электрический ток, называемый зарядным емкостным током I зар.
Зарядный ток в цени протекает обычно тысячные доли секунды до тех пор, пока напряжение на конденсаторе достигнет величины, равной э. д. с. генератора. График нарастания напряжения на обкладках конденсатора в процессе его заряда представлен на рис. 2,а, из которого видно, что напряжение Uc плавно увеличивается, сначала быстро, а затем все медленнее, пока не станет равным э. д. с. генератора Е. После этого напряжение на конденсаторе остается неизменным.
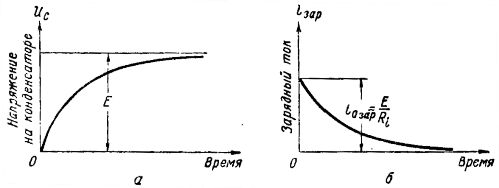
Рис. 2. Графики напряжения и тока при заряде конденсатора
Пока конденсатор заряжается, по цепи проходит зарядный ток. График зарядного тока показан на рис. 2,б. В начальный момент зарядный ток имеет наибольшую величину, потому что напряжение на конденсаторе еще равно нулю, и по закону Ома io зар = E/ R i , так как вся э. д. с. генератора приложена к сопротивлению R i.
По мере того как конденсатор заряжается, т. е. возрастает напряженно на нем, для зарядного тока уменьшается. Когда напряженно па конденсаторе уже имеется, падение напряжения на сопротивление будет равно разности между э. д. с. генератора и напряжением на конденсаторе, т. е. равно Е – U с. Поэтому i зар = (E-Uс)/R i
Отсюда видно, что с увеличением Uс уменьшается i зар и при Uс = E зарядный ток становится равным нулю.
Про закон Ома подробнее смотрите здесь: закон Ома для участка цепи
Продолжительность процесса заряда конденсатора зависит от двух величии:
1) от внутреннего сопротивления генератора R i ,
2) от емкости конденсатора С.
На рис. 2 показаны графики нарядных токов для конденсатора емкостью 10 мкф: кривая 1 соответствует процессу заряда от генератора с э. д. с. Е = 100 В и с внутренним сопротивлением R i = 10 Ом, кривая 2 соответствует процессу заряда от генератора с такой же э. д. с, но с меньшим внутренним сопротивлением: R i = 5 Ом.
Из сравнения этих кривых видно, что при меньшем внутреннем сопротивлении генератора сила нарядного тока в начальный момент больше, и поэтому процесс заряда происходит быстрее.
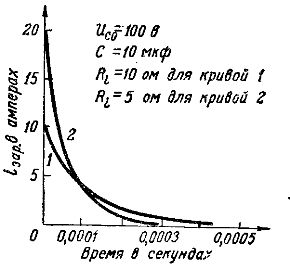
Рис. 2. Графики зарядных токов при разных сопротивлениях
На рис. 3 дается сравнение графиков зарядных токов при заряде от одного и того же генератора с э. д. с. Е = 100 В и внутренним сопротивлением R i = 10 ом двух конденсаторов разной емкости: 10 мкф (кривая 1) и 20 мкф (кривая 2).
Величина начального зарядного тока io зар = Е/ Ri = 100/10 = 10 А одинакова для обоих конденсаторов, по так как конденсатор большей емкости накапливает большее количество электричества, то зарядный его ток должен проходить дольше, и процесс заряда получается более длительным.
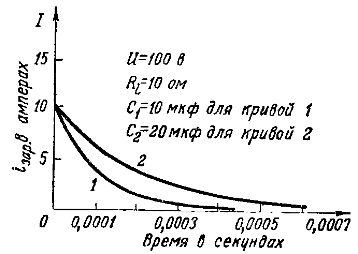
Рис. 3. Графики зарядных токов при разных емкостях
Отключим заряженный конденсатор от генератора и присоединим к его обкладкам сопротивление.
На обкладках конденсатора имеется напряжение U с, поэтому в замкнутой электрической цепи потечет ток, называемый разрядным емкостным током i разр.
Ток идет от положительной обкладки конденсатора через сопротивление к отрицательной обкладке. Это соответствует переходу избыточных электронов с отрицательной обкладки на положительную, где их недостает. Процесс рам ряда происходит до тех пор, пока потенциалы обеих обкладок не сравняются, т. е. разность потенциалов между ними станет равном нулю: Uc=0 .
На рис. 4, а показан график уменьшения напряжения на конденсаторе при разряде от величины Uc о =100 В до нуля, причем напряжение уменьшается сначала быстро, а затем медленнее.
На рис. 4,б показан график изменения разрядного тока. Сила разрядного тока зависит от величины сопротивления R и по закону Ома i разр = Uc / R
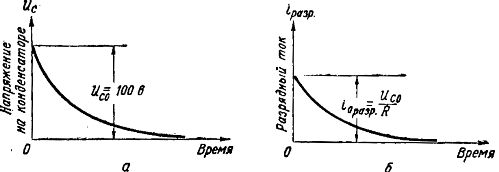
Рис. 4. Графики напряжения и токов при разряде конденсатора
В начальный момент, когда напряжение па обкладках конденсатора наибольшее, сила разрядного тока также наибольшая, а с уменьшением Uc в процессе разряда уменьшается и разрядный ток. При Uc=0 разрядный ток прекращается.
Продолжительность разряда зависит:
1) от емкости конденсатора С
2) от величины сопротивления R , на которое конденсатор разряжается.
Чем больше сопротивление R , тем медленнее будет происходить разряд. Это объясняется тем, что при большом сопротивлении сила разрядного тока невелика и величина заряда на обкладках конденсатора уменьшается медленно.
Это можно показать на графиках разрядного тока одного и того же конденсатора, имеющего емкость 10 мкф и заряженного до напряжения 100 В, при двух разных величинах сопротивления (рис. 5): кривая 1 — при R = 40 Ом, i оразр = Uc о/ R = 100/40 = 2,5 А и кривая 2 – при 20 Ом i оразр = 100/20 = 5 А.
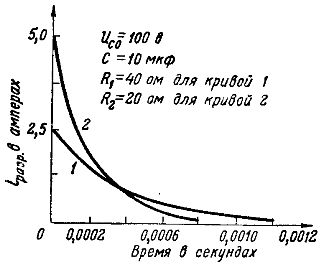
Рис. 5. Графики разрядных токов при разных сопротивлениях
Разряд происходит медленнее также тогда, когда емкость конденсатора велика. Получается это потому, что при большей емкости на обкладках конденсатора имеется большее количество электричества (больший заряд) и для стекания заряда потребуется больший промежуток времени. Это наглядно показывают графики разрядных токов для двух конденсаторов раиной емкости, заряженных до одного и того же напряжения 100 В и разряжающихся на сопротивление R =40 Ом (рис. 6 : кривая 1 — для конденсатора емкостью 10 мкф и кривая 2 — для конденсатора емкостью 20 мкф).
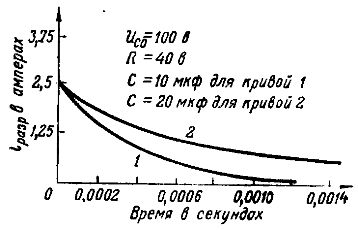
Рис. 6. Графики разрядных токов при разных емкостях
Из рассмотренных процессов можно сделать вывод, что в цепи с конденсатором ток проходит только в моменты заряда и разряда, когда напряжение на обкладках меняется.
Объясняется это тем, что при изменении напряжения изменяется величина заряда на обкладках, а для этого требуется перемещение зарядов по цепи, т. е. по цепи должен проходить электрический ток. Заряженный конденсатор не пропускает постоянный ток, так как диэлектрик между его обкладками размыкает цепь.
В процессе заряда конденсатор накапливает энергию, получая ее от генератора. При разряде конденсатора вся энергия электрического поля переходит в тепловую энергию, т. е. идет на нагрев сопротивления, через которое разряжается конденсатор. Чем больше емкость конденсатора и напряжение на его обкладках, тем больше будет энергия электрического поля конденсатора. Величина энергии, которой обладает конденсатор емкостью С, заряженный до напряжения U, равна: W = W с = С U 2 /2
Пример. Конденсатор С=10 мкф заряжен до напряжении U в = 500 В. Определить энергию, которая выделится в вило тепла на сопротивлении, через которое разряжается конденсатор.
Решение. Пpи разряде вся энергия, запасенная конденсатором, перейдет в тепловую. Поэтому W = W с = С U 2 /2 = (10 х 10 -6 х 500)/2 = 1,25 дж.