У металлов, не обладающих сверхпроводимостью, при низких температурах из-за наличия примесей наблюдается область 1 – область остаточного сопротивления, почти не зависящая от температуры (рис. 10.5). Остаточное сопротивление – r ост тем меньше, чем чище металл.
Рис. 10.5. Зависимость удельного сопротивления металла от температуры
Быстрый рост удельного сопротивления при низких температурах до температуры Дебая Q д может быть объяснен возбуждением новых частот тепловых колебаний решетки, при которых происходит рассеяние носителей заряда – область 2.
При Т > Q д , когда спектр колебаний возбужден полностью, увеличение амплитуды колебаний с ростом температуры приводит к линейному росту сопротивления примерно до Т пл – область 3. При нарушении периодичности структуры электрон испытывает рассеяние, приводящее к изменению направления движения, конечным длинам свободного пробега и проводимости металла. Энергия электронов проводимости в металлах составляет 3–15 эВ, что соответствует длинам волн 3–7 Å. Поэтому любые нарушения периодичности, обусловленные примесями, дефектами, поверхностью кристалла или тепловыми колебаниями атомов (фононами) вызывают рост удельного сопротивления металла.
Проведем качественный анализ температурной зависимости удельного сопротивления металлов. Электронный газ в металлах является вырожденным и основным механизмом рассеяния электронов в области высоких температур является рассеяние на фононах.
При понижения температуры до абсолютного нуля сопротивление нормальных металлов стремится к постоянному значению – остаточному сопротивлению. Исключением из этого правила являются сверхпроводящие металлы и сплавы, в которых сопротивление исчезает ниже некоторой критической температуры Тсв (температура перехода в сверхпроводящее состояние).
При увеличении температуры, отклонение удельного сопротивления от линейной зависимости у большинства металлов наступает вблизи температуры плавления Тпл . Некоторое отступление от линейной зависимости может наблюдаться у ферромагнитных металлов, в которых происходит дополнительное рассеяние электронов на нарушениях спинового порядка.
При достижении температуры плавления и переходе в жидкое состояние у большинства металлов наблюдается резкое увеличение удельного сопротивления и у некоторых его уменьшение. Если плавление металла или сплава сопровождается увеличением объема, то удельное сопротивление повышается в два–четыре раза (например, у ртути в 4 раза).
У металлов, объем которых при плавлении уменьшается, наоборот, происходит понижение удельного сопротивления (у галлия на 53%, у сурьмы –29% и у висмута –54%) . Подобная аномалия может быть объяснена возрастанием плотности и модуля сжимаемости при переходе этих металлов из твердого в жидкое состояние. У некоторых расплавленных (жидких) металлов удельное сопротивление с ростом температуры при постоянном объеме перестает расти, у других оно растет более медленно, чем в твердом состоянии. Такие аномалии, по-видимому, можно связать с явлениями разупорядочения решетки, которые неодинаково происходят в различных металлах при переходе их из одного агрегатного состояния в другое.
Важной характеристикой металлов является температурный коэффициент удельного электрического сопротивления, показывающий относительное изменение удельного сопротивления при изменении температуры на один Кельвин (градус)
ar– положительно, когда удельное сопротивление возрастает при повышении температуры. Очевидно, что величина ar также является функцией температуры. В области 3 линейной зависимости r ( T ) (см. рисунок 10.3) выполняется соотношение:
где r0 и ar– удельное сопротивление и температурный коэффициент удельного сопротивления при температуре T 0 , а r – удельное сопротивление при температуре T . Экспериментальные данные показывают, что у большинства металлов ar при комнатной температуре примерно 0,004 К -1 .У ферромагнитных металлов значение ar несколько выше.
Остаточное удельное сопротивление металлов. Как говорилось выше, сопротивление нормальных металлов стремится к постоянному значению — остаточному сопротивлению, по мере снижения температуры до абсолютного нуля. У нормальных металлов (не сверхпроводников) остаточное сопротивление возникает из-за рассеяния электронов проводимости статическими дефектами
Общую чистоту и совершенство металлического проводника можно определять отношением сопротивлений r =R273/R4,2 K . Для стандартной меди чистоты 99,999 это отношение составляет 1000. Б óльших значений r можно достигнуть путем дополнительных зонных переплавок и приготовлением образцов в виде монокристаллов.
Обширный экспериментальный материал содержит многочисленные данные по измерению сопротивления в металлах, вызванному наличием в них примесей. Можно отметить следующие наиболее характерные изменения в металлах, вызываемые легированием. Во-первых, не считая фононных возмущений, примесь является локальным нарушением идеальности решетки совершенное во всех других отношениях. Во-вторых, легирование влияет на зонную структуру, сдвигая энергию Ферми и изменяя плотность состоянии и эффективную массу, т.е. параметры, частично определяющие идеальное сопротивление металла. В-третьих, легирование может менять упругие константы и, соответственно, колебательный спектр решетки, оказывая влияние на идеальное сопротивление.
Общее удельное сопротивление проводника при температурах выше 0К складывается из остаточного сопротивления r ост и удельного сопротивления, обусловленного рассеянием на тепловых колебаниях решетки – r Т
Это соотношение известно как правило Матиссена об аддитивности удельного сопротивления. Часто, однако, наблюдаются значительные отклонения от правила Матиссена , причем некоторые их этих отклонений могут говорить не в пользу применимости основных факторов, влияющих на сопротивление металлов при введении в них примесей. Однако второй и третий факторы, отмеченные в начале этого раздела, также дают заметный вклад. Но, все же более сильное воздействие на сопротивление разбавленных твердых растворов оказывает первый фактор.
Изменение остаточного сопротивления на 1 ат . % примеси для одновалентных металлов можно найти по правилу Линде, согласно которому
где a и b – константы, зависящие от природы металла и периода, который занимает в Периодической системе элементов примесный атом; ΔΖ – разность валентностей металла-растворителя и примесного атома. Значительный практический интерес представляют расчеты сопротивления, обусловленные вакансиями и внедренными атомами. Такие дефекты легко возникает при облучении образца частицами высоких энергий, например нейтронами из реактора или ионами из ускорителя.
На основании классической электронной теории проводимости металлов можно объяснить закон Джоуля-Ленца.
Упорядоченное движение электронов происходит под действием сил поля. Как и выше, будем считать, что в момент соударения с положительными ионами кристаллической решётки электроны полностью передают ей свою кинетическую энергию. К концу свободного пробега скорость электрона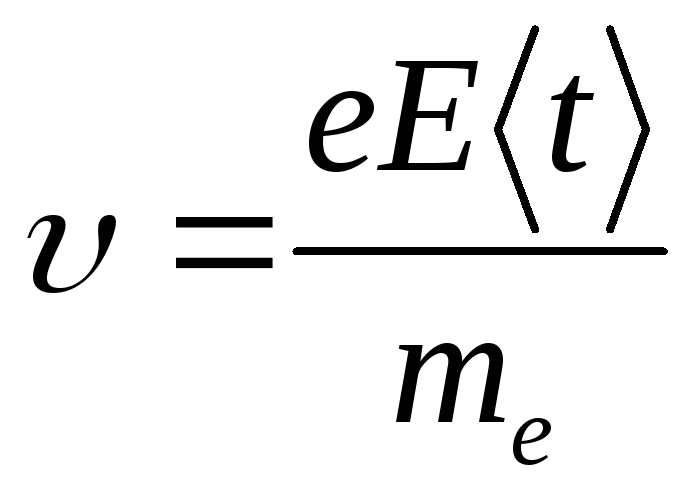 
, а кинетическая энергия
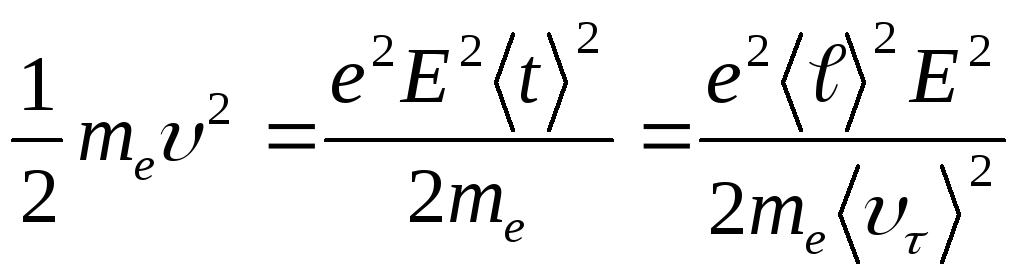(14.9)
Мощность, выделяемая единицей объёма металла (плотность мощности), равна произведению энергии одного электрона на число соударений в секунду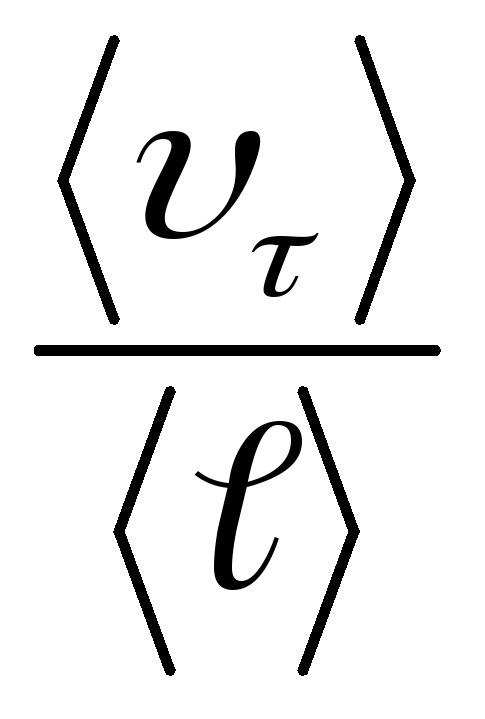
и на концентрациюn электронов:
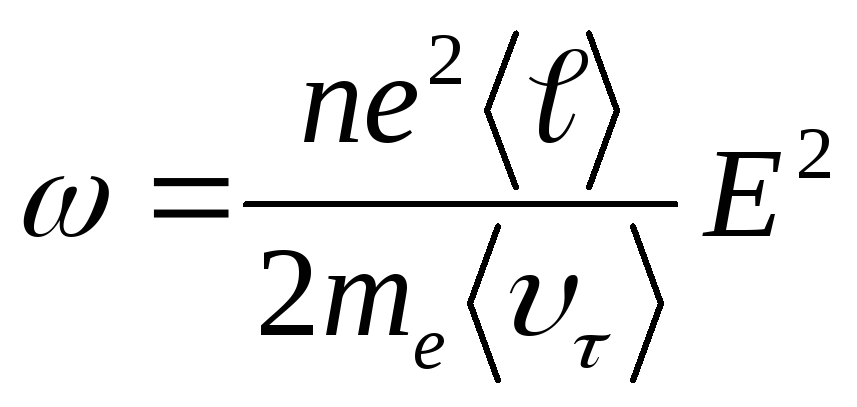(14.10)
Учитывая (14.7), имеем
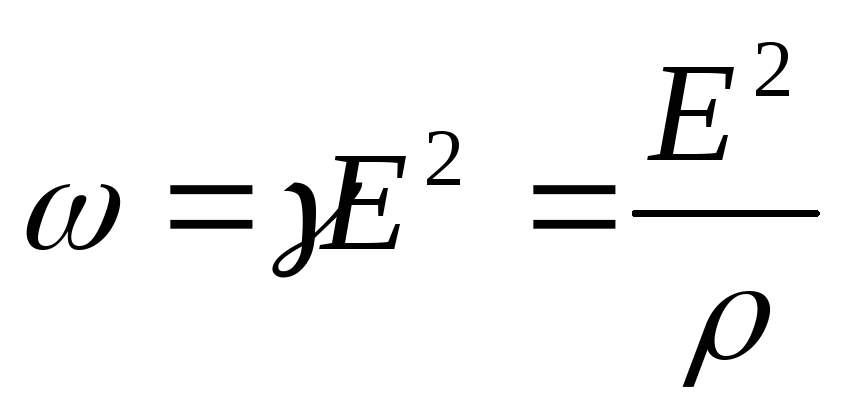
– закон Джоуля-Ленца в дифференциальной форме.
Если нас интересует энергия, выделяемая проводником длиной ℓ, площадью поперечного сечения S за промежуток времени dt, то выражение (14.10) нужно умножить на объём проводника V=St и время dt:
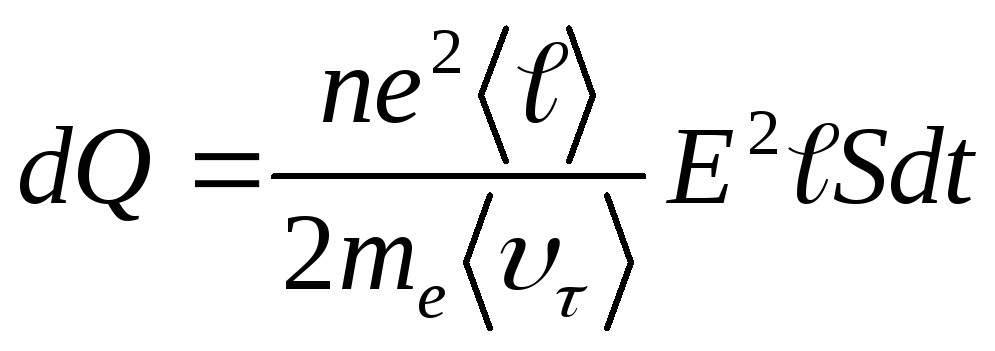
Учитывая, что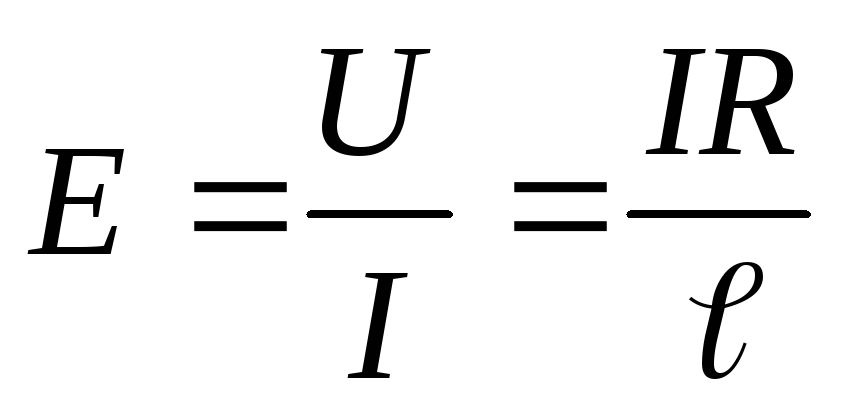 
(гдеR– сопротивление проводника), получаем закон Джоуля-Ленца в виде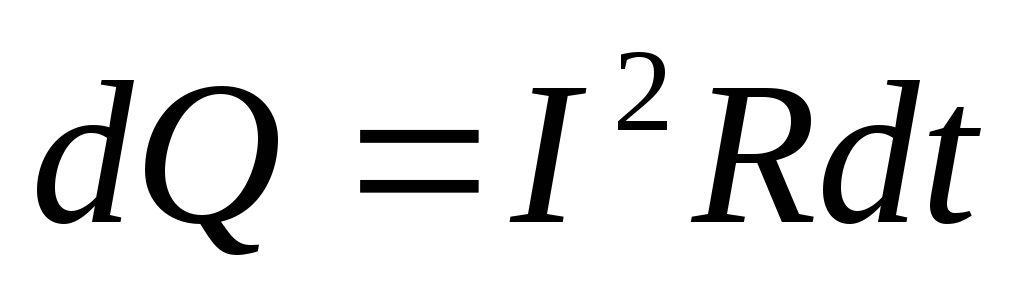 
§ 14.3 Зависимость сопротивления металлов от температуры. Сверхпроводимость. Закон Видемана-Франца
Удельное сопротивление зависит не только от рода вещества, но и от его состояния, в частности, от температуры. Зависимость удельного сопротивления от температуры можно охарактеризовать, задавая температурный коэффициент сопротивления данного вещества:
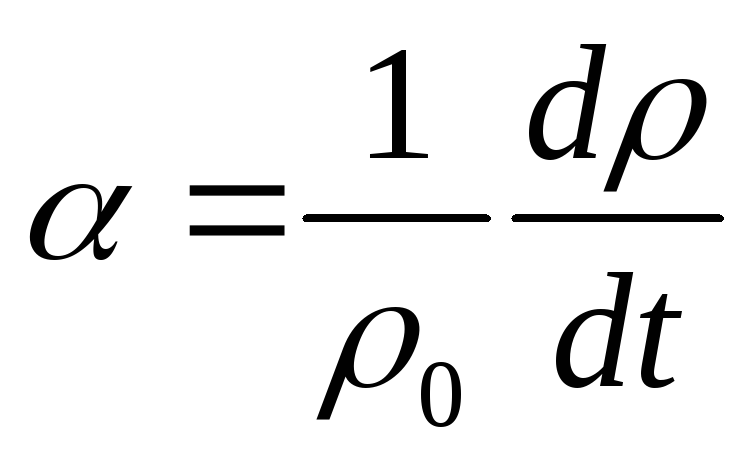(14.11)
Он даёт относительное приращение сопротивления при увеличении температуры на один градус.
Температурный коэффициент сопротивления для данного вещества различен при разных температурах. Это показывает, что удельное сопротивление изменяется с температурой не по линейному закону, а зависит от неё более сложным образом.
где ρ0 – удельное сопротивление при 0ºС, ρ – его значение при температуре tºС.
Температурный коэффициент сопротивления может быть как положительным, так и отрицательным. У всех металлов сопротивление увеличивается с увеличением температуры, а следовательно для металлов
α >0. У всех электролитов в отличии от металлов сопротивление при нагревании всегда уменьшается. Сопротивление графита с повышением температуры также уменьшается. Для таких веществ α , т.е. чем больше , тем меньшую помеху для упорядоченного движения электронов представляют соударения. Электропроводимость обратно пропорциональна средней тепловой скорости . Тепловая скорость при повышении температуры возрастает пропорционально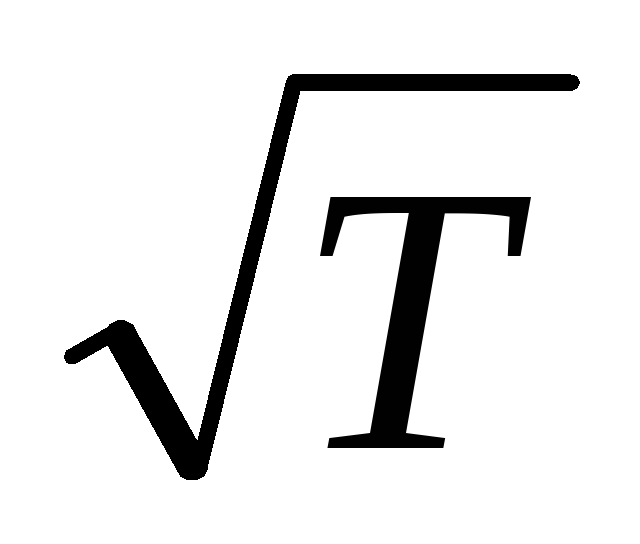 
, что приводит к уменьшению электропроводимости и увеличению удельного сопротивления проводников. Анализируя формулу (14.7), можно, кроме того, объяснить зависимость γ и ρ от рода проводника.
При очень низких температурах порядка 1-8ºК сопротивление некоторых веществ резко падает в миллиарды раз и практически становится равным нулю.
Это явление, впервые открыто голландским физиком Г.Камерлинг-Оннесом в 1911 г.. называется сверхпроводимостью. В настоящее время сверхпроводимость установлена у целого ряда чистых элементов (свинца, олова, цинка, ртути, алюминия и др), а также у большого числа сплавов этих элементов друг с другом и с другими элементами. На рис. 14.3 схематически показана зависимость сопротивления сверхпроводников от температуры.
Теория сверхпроводимости была создана в 1958 г. Н.Н. Боголюбовым. Согласно этой теории, сверхпроводимость – это движение электронов в кристаллической решётке без соударений друг с другом и с атомами решётки. Все электроны проводимости движутся как один поток невязкой идеальной жидкости, не взаимодействуя между собой и с решёткой, т.е. не испытывая трения. Поэтому сопротивление сверхпроводников равно нулю. Сильное магнитное поле, проникая в сверхпроводник, отклоняет электроны, и, нарушая «ламинарное течение» электронного потока, вызывает соударение электронов с решёткой, т.е. возникает сопротивление.
В сверхпроводящем состоянии между электронами происходит обмен квантами энергии, что приводит к созданию между электронами сил притяжения, которые больше кулоновских сил отталкивания. При этом образуются пары электронов (куперовские пары) с взаимно скомпенсированными магнитными и механическими моментами. Такие пары электронов движутся в кристаллической решётке без сопротивления.
Одним из важнейших практических применений сверхпроводимости является применение её в электромагнитах со сверхпроводящей обмоткой. Если бы не существовало критического магнитного поля, разрушающего сверхпроводимость, то с помощью таких электромагнитов можно было бы получать магнитные поля в десятки и сотни миллионов ампер на сантиметр. Получать такие большие постоянные поля с помощью обычных электромагнитов невозможно, так как для этого потребовались бы колоссальные мощности, и был бы практически невозможен отвод тепла, выделяемого при поглощении обмоткой столь больших мощностей. В сверхпроводящем электромагните расход мощности источника тока ничтожен, а расход мощности на охлаждение обмотки до гелиевой температуре (4,2ºК) на четыре порядка ниже, чем в обычном электромагните, создающем такие же поля. Сверхпроводимость применяется и для создания систем памяти электронных математических машин (криотронные элементы памяти).
В 1853 г. Видеман и Франц опытным путём установили, что отношение теплопроводности λ к электропроводности γ для всех метал лов при одной и той же температуре одинаково и пропорционально их термодинамической температуре.
Это заставляет предполагать, что теплопроводность в металлах, так же как и электропроводность, обусловлена движением свободных электронов. Будем считать, что электроны подобны одноатомному газу, коэффициент теплопроводности которого, согласно кинетической теории газов, равен
(14.13)
(n – концентрация атомов, m -масса атома, -средняя длина свободного пробега электрона, cV-удельная теплоёмкость).
Для одноатомного газа
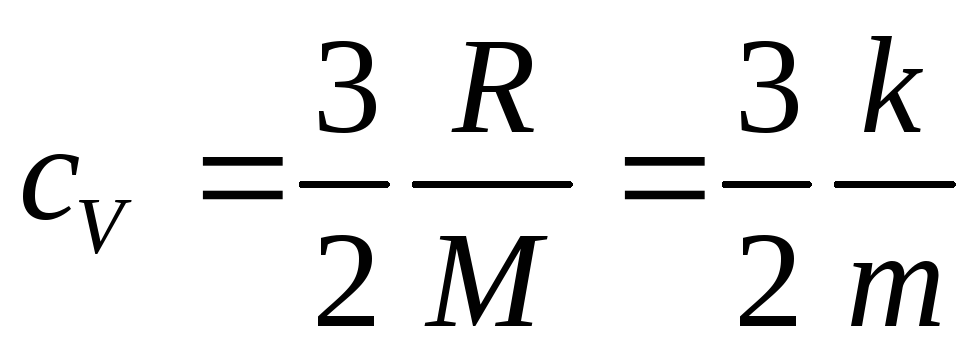
(k -постоянная Больцмана, М –молярная масса).
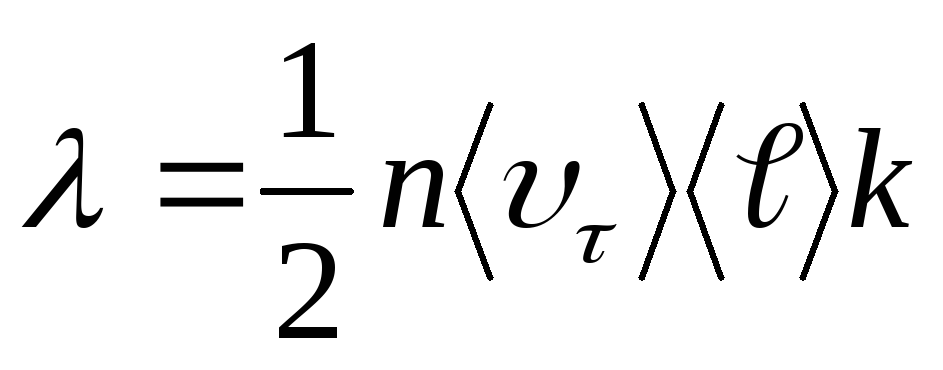(14.14)
Из уравнений (14.7) и (14.14) находим отношение теплопроводности и электропроводности металла:
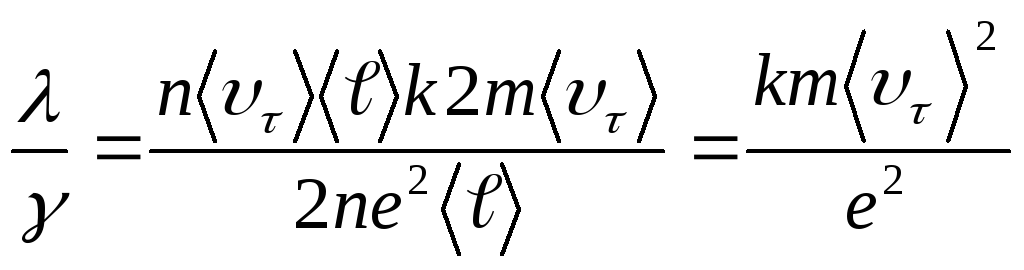(14.15)
Из кинетической теории газов известно, что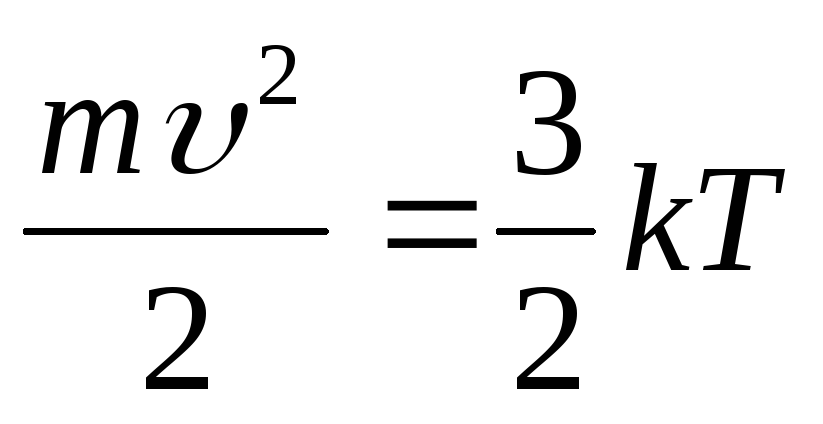 
, тогда
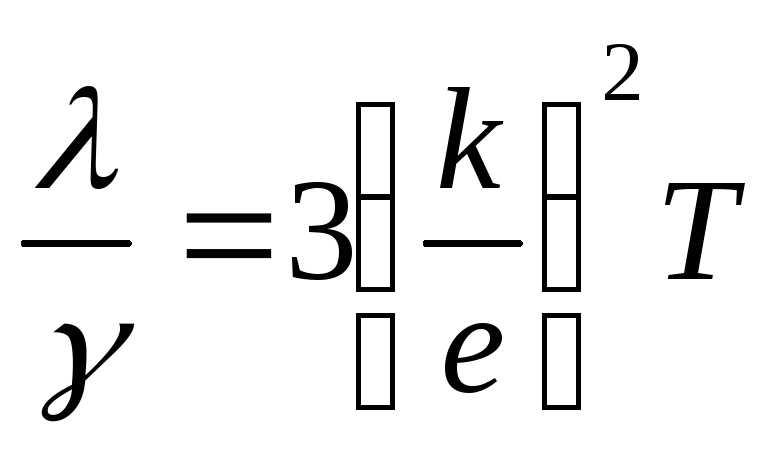(14.16)
( k и е – постоянные величины).
Поэтому отношение теплопроводности и электропроводности металла пропорционально термодинамической температуре, что и было установлено законом Видемана-Франца. Так как k =1,38∙10 -23 Дж/К; е = 1,6∙10 -19 Кл, то
(14.17)
Закон Видемана-Франца для большинства металлов выполняется при температуре 100-400 К, но при низкой температуре закон существенно нарушается. Имеются металлы (бериллий, марганец) которые совсем не подчиняются закону Видемана-Франца. Выход из непреодолимых противоречий был найден в квантовой электронной теории металлов.
Практически в электротехнике выло выявлено, что с увеличением температуры сопротивление проводников из металла возрастает, а с понижением уменьшается. Для всех проводников из металла это изменение сопротивления почти одинаково и в среднем равно 0,4% на 1°С.
Если быть точным, то на самом деле при изменении температуры проводника изменяется его удельное сопротивление, которое имеет следующую зависимость:
где ρ и ρ0, R и R0 – соответственно удельные сопротивления и сопротивления проводника при температурах t и 0°С (шкала Цельсия), α – температурный коэффициент сопротивления, [α] = град -1 .
Изменение удельного сопротивления проводника приводит к изменения самого сопротивления, что видно из следующего выражения:
Зная электронную теорию строения вещества можно дать следующее объяснение увеличению сопротивления металлических проводников с повышением температуры. При увеличении температуры проводник получает тепловую энергию, которая несомненно передается всем атомам вещества, в результате чего .возрастает их тепловое движение. Увеличившееся тепловое движение атомов создает большее сопротивление направленному движению свободных электронов (увеличивается вероятность столкновения свободных электронов с атомами), от этого и возрастает сопротивление проводника.
С понижением температуры направленное движение электронов облегчается (уменьшается возможность столкновения свободных электронов с атомами), и сопротивление проводника уменьшается. Этим объясняется интересное явление — сверхпроводимость металлов. Сверхпроводимость, т. е. уменьшение сопротивления металлов до нуля, наступает при огромной отрицательной температуре —273° С, называемой абсолютным нулем. При температуре абсолютного нуля атомы металла как бы застывают на месте, совершенно не препятствуя движению электронов.
График звисимости сопротивления металлического проводника от температуры представлен на рисунке 1.
Рисунок 1. График зависимости удельного сопротивления металлического проводника от температуры
Необходимо сказать, что сопротивление электролитов и полупроводников (уголь, селен и другие) с увеличением температуры уменьшается.
Температурная зависимость сопротивления электролита объясняется также в основном изменением удельного сопротивления,однако всегда температурный коэффициент сопротивления – α
Поэтому кривая зависимости сопротивленя электролита от температуры имеет вид, представленый на рисунке 2.
Рисунок 1. График зависимости удельного сопротивления электролита от температуры
Ддя полупроводников характер изменения удельного сопротивления от температуры будет схож с таковым для элетролитов.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!