Аксонометрия что это такое

Аксонометрия – особый отдел в черчении, в нем изучается то, как получить наглядное изображение предметов на плоскости. Аксонометрическая проекция выглядит как точный рисунок предмета. Аксонометрия, расшифровывается как измерение по осям.

Проекции в аксонометрии разделяют на несколько видов:

1) Прямоугольная – это когда проецируемые прямые, перпендикулярные к плоскости акс.проекции. Так же в этот вод входят – диметрическая и изометрическая.

2) Косоугольная – этом когда прямые идут не под углом 90 0 относительно акс. проекции. Так же в этот вид входит проекция фронтальная диметрическая.

Во время выполнения переноса предмета на проекцию, возможно искажение осей.

Помощь в ознакомлении с учебником или с любой книгой по которой учатся предоставляет сайт – учебник pdf (http://ruscopybook.com/). Публикация изданий позволяет учителям ознакомиться с существующими учебно-методическими комплектами и выбрать подходящий для преподавания. Родителям – готовые домашние задания.

Чаще всего используются в работе, косоугольная фронтальная диметрическая и изометрическая проекции, потому что они являются наиболее простыми. Их мы и разберем. По другим предметам поможет разобраться сайт учебник pdf (http://ruscopybook.com/).

– Косоугольная фронтальная диметрическая проекция.
для данной проекции искажение на оси у – 0,5, на оси х и z = 0. Это означает что высота и длина отмеряются в натуральные, а ширина отмеряется с уменьшением в два раза.

– Прямоугольная изометрическая проекция
Данная проекция обладает преимуществом так как данные не искажаются на всех осях. То есть имеет одинаковое измерение по всем осям, соответственно и размеры предмета, на осях откладываются натуральные.

Для того что бы получить аксонометрическую проекцию, нужно расположить предмет в системе координатных осей, перед акс.плоскостью. Дать проецируемое направление и провести через все точки мысленно, лучи до пересечения с плоскостью.

– Изометрическая Прямоугольная
Перемещаем предмет в угол координат и ставим его так что бы наклон сторон был равным к акс. плоскости. Проводим невидимые лучи через точки, под углом девяносто градусов, до пересечения с плоскостью.

– Косоугольная фронтальная диметрическая проекция.
Рядом с P-плоскостью ставим предмет, чтобы передняя сторона находилась фронтально к плоскости. Проводим лучи параллельные, относительно плоскости под острым углом. Получаем координатные оси и проекцию предмета косоугольную фронтальную диметрическую.

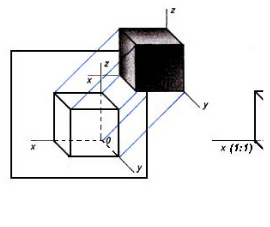
Для чего нужно уметь правильно переносить плоские фигуры на проекцию?
Плоской фигурой называются те фигуры у которых точки входят в одну плоскость. На пример – прямоугольник, ромб, квадрат и другие. Умение строить на проекции треугольник, квадраты, трапецию и шестиугольников очень нужно для того чтобы построить модели, детали и проекции геометрического тела.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Большая советская энциклопедия. — М.: Советская энциклопедия . 1969—1978 .

Смотреть что такое “Аксонометрия” в других словарях:

Аксонометрия — Аксонометрия. АКСОНОМЕТРИЯ (от греческого axon ось и . метрия), способ изображения предметов на плоскости с фиксированным искажением размеров в каждом из трех направлений (длина, ширина, высота). … Иллюстрированный энциклопедический словарь

АКСОНОМЕТРИЯ — (греч.). Измерение осей кристаллов. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. аксонометрия [гр. ось + мерю] – способ изображения предметов на чертеже, при котором на плоскость изображений проектируется как… … Словарь иностранных слов русского языка

аксонометрия — и ж. axonométrie f. <гр. Способ изображения предметов на чертеже, при котором на плоскость изображений проектируется как самый предмет, так и оси прямоугольной системы координат, к которыми изображаемый предмет отнесен. СИС 1954. План этот… … Исторический словарь галлицизмов русского языка

Аксонометрия — один из методов проецирования (получения проекции предмета на плоскости), с помощью которого наглядно изображают пространственные тела на плоскости бумаги. А. Делится на три вида: 1) изометрию (измерение по всем трем координатным осям… … Издательский словарь-справочник

АКСОНОМЕТРИЯ — (от греческого axon ось и. метрия), способ изображения предметов на плоскости с фиксированным искажением размеров в каждом из трех направлений (длина, ширина, высота) … Современная энциклопедия

АКСОНОМЕТРИЯ — (от греч. axon ось и . метрия) способ изображения предметов на чертеже при помощи параллельных проекций, состоящий в том, что предмет изображается на плоскости вместе с пространственной системой координат, к которой он отнесен, и его проекцией… … Большой Энциклопедический словарь

аксонометрия — Способ изображения предмета на чертеже при помощи параллельного проецирования с определённым искажением размеров по осям проекций. [http://sl3d.ru/o slovare.html] Тематики машиностроение в целом … Справочник технического переводчика

АКСОНОМЕТРИЯ — способ изображения предмета на плоскости (см.) с помощью параллельного проецирования с определённым искажением размеров по осям проекций. В зависимости от углов наклона между осями аксонометрических координат и от длины единичных отрезков… … Большая политехническая энциклопедия

Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими.

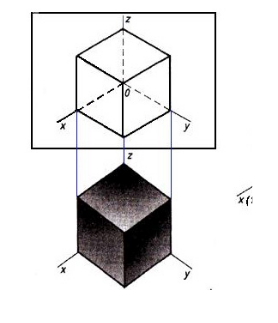
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).

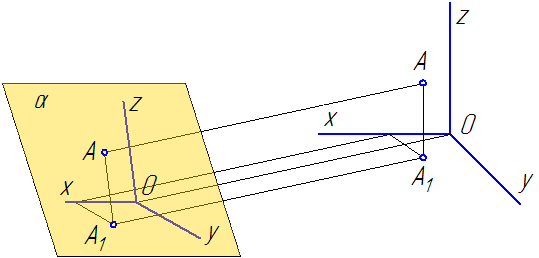
Рисунок 4.1
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.

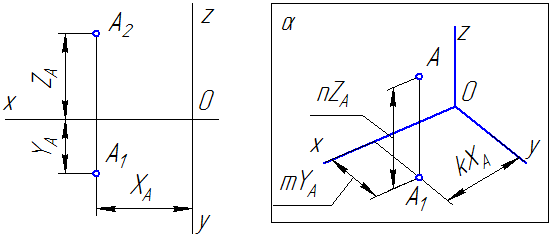
Рисунок 4.2
Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:

• прямоугольные изометрические и диметрические;
• косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;

Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.

4.1. Прямоугольные проекции

4.1.1. Изометрическая проекция

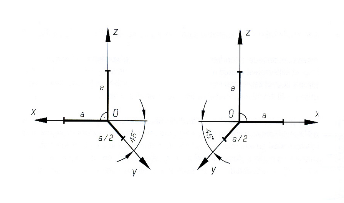
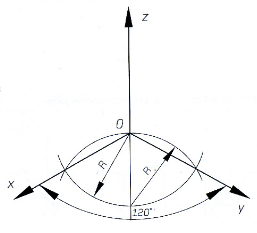
Направление аксонометрических осей приведено на Рисунке 4.3.

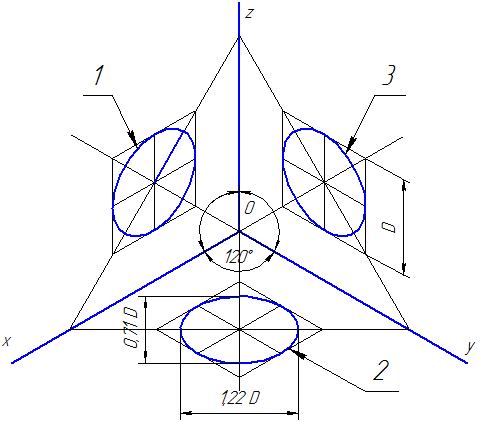
Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции

Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.

Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

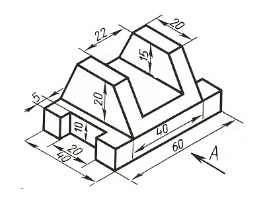
Пример выполнения изометрической проекции условной детали с вырезом приводится на  Рисунке 4.4.

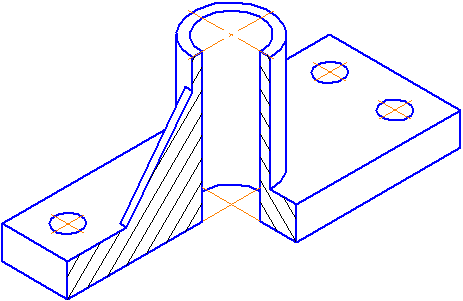
Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции

4.1.2. Диметрическая проекция

Положение аксонометрических осей проводится на Рисунке 4.5.

Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.

Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.

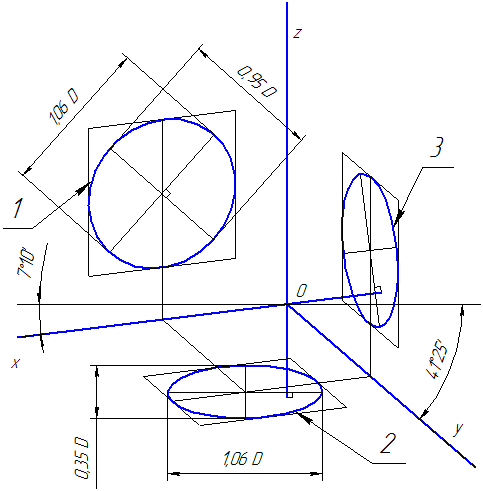
Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции

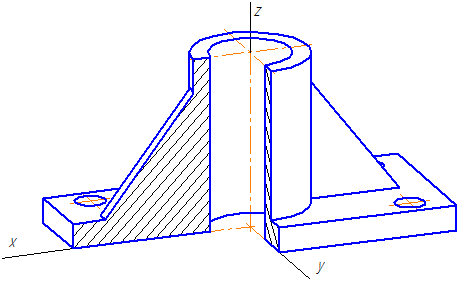
Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции

4.2 Косоугольные проекции

4.2.1 Фронтальная диметрическая проекция

Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 30 0 и 60 0 .

Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.

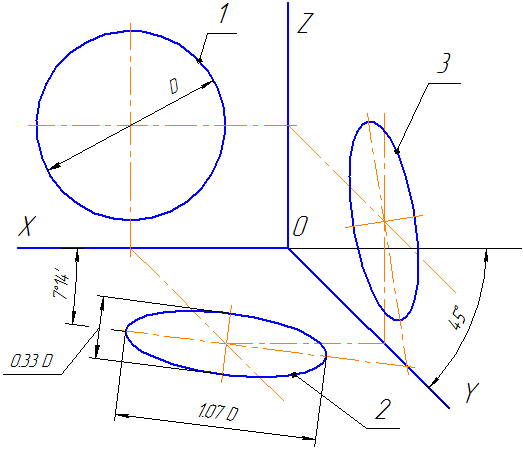
Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.

Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.

Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.

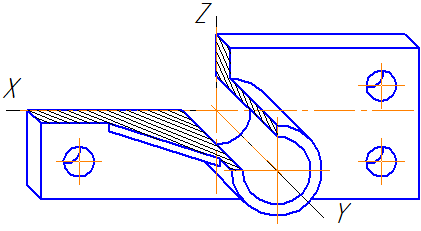
Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции

4.3 Построение эллипса

4.3.1 Построения эллипса по двум осям

На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).

Одна из этих окружностей делится на несколько равных (или неравных) частей.

Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.

Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.

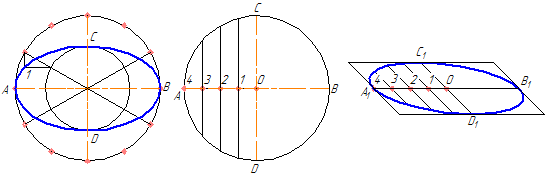
а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)

4.3.2 Построение эллипса по хордам

Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А₁В₁=АВ и С₁ D₁ = 0,5CD. Диаметр А ₁В₁ делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).

4.4 Штриховка сечений

Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).

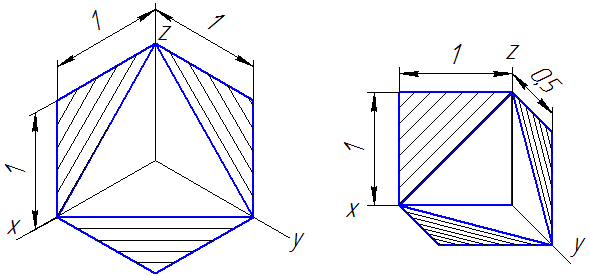
а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях

Представляем вашему вниманию лекцию по теме аксонометрия: