Алгебраическая сумма токов в узле равна нулю

Закон Кирхгофа (правила Кирхгофа), сформулированные Густавом Кирхгофом в 1845 году, являются следствиями из фундаментальных законов сохранения заряда и безвихревости электростатического поля.

Закон Кирхгофа – это соотношения, выполняемые между токами и напряжениями на участках любых электрических цепей. Они позволяют рассчитывать любые электрические цепи: постоянного, переменного или квазистационарного тока.

При формулировании правил Кирхгофа используют такие понятия, как ветвь, контур и узел электрической цепи.

• Ветвь – участок электрической цепи с одни и тем же током.
• Узел – точка соединения трех или более ветвей.
• Контур – замкнутый путь, проходящий через несколько узлов и ветвей разветвлённой электрической цепи.

При обходе надо учесть, что ветвь и узел могут одновременно принадлежать нескольким контурам. Правила Кирхгофа справедливы как для линейных, так и для нелинейных цепей при любом характере изменения во времени токов и напряжений. Правила Кирхгофа широко применяются при решении задач электротехники за счет легкости в расчетах.

1 закон Кирхгофа

В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, сопротивлением и ЭДС всей цепи или на каком-либо участке цепи определяются законом Ома. Но на практике в цепях токи от какой-либо точки идут по разным путям (Рис. 1). Поэтому становиться актуальным введение новых правил для проведения расчетов электрических цепей.

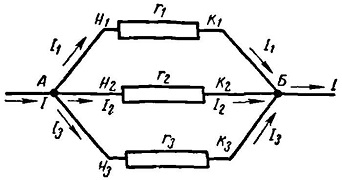
Рис. 1. Схема параллельного соединения проводников.

Так, при параллельном соединении проводников начала всех проводников соединены в одну точку, а концы проводников – в другую точку. Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.

Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А, растекается далее по трем сопротивлениям и равен сумме токов, выходящих из этой точки: I = I1 + I2 + I3.

Согласно первому правилу Кирхгофа алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла – отрицательным.

Запишем первый закон Кирхгофа в комплексной форме:

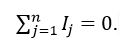
Первый закон Кирхгофа гласит, что алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла. То есть, сколько тока втекает в узел, столько же вытекает (как следствие закона сохранения электрического заряда). Алгебраическая сумма – это сумма, в которую входят слагаемые со знаком плюс и со знаком минус.

Рис. 2. i_1+i_4=i_2+i_3.

Рассмотрим применение 1 закона Кирхгофа на следующем примере:

• I1 – это полный ток, текущий к узлу А, а I2 и I3 — токи, вытекающие из узла А.
• Тогда мы можем записать: I1 = I2 + I3.
• Аналогично для узла B: I3 = I4 + I5.
• Пусть, что I4 = 5 А и I5 = 1 А, получим: I3 = 5 + 1 = 6 (А).
• Пусть I2 = 10 А, получим: I1 = I2 + I3 = 10 + 6 = 16 (А).
• Запишем подобное соотношение для узла C: I6 = I4 + I5 = 5 + 1 = 6 А.
• А для узла D: I1 = I2 + I6 = 10 + 6 = 16 А
• Таким образом мы наглядно видим справедливость первого закона Кирхгофа.

2 закон Кирхгофа

При расчете электрических цепей в большинстве случаев нам встречаются цепи, образующие замкнутые контуры. В состав таких контуров, кроме сопротивлений, могут входить ЭДС (источники напряжений). На рисунке 4 представлен участок такой электрической цепи. Произвольно выбираем положительные направления токов. Обходим контур от точки А в произвольном направлении (выберем по часовой стрелке). Рассмотрим участок АБ: происходит падение потенциала (ток идет от точки с высшим потенциалом к точке с низшим потенциалом).

• На участке АБ: φА + E1 – I1r1 = φБ.
• БВ: φБ – E2 – I2r2 = φВ.
• ВГ: φВ – I3r3 + E3 = φГ.
• ГА: φГ – I4r4 = φА.
• Складывая данные уравнения, получим: φА + E1 – I1r1 + φБ – E2 – I2r2 + φВ – I3r3 + E3 + φГ – I4r4 = φБ + φВ + φГ + φА
• или: E1 – I1r1 – E2 – I2r2 – I3r3 + E3 – I4r4 = 0.
• Откуда имеем следующее: E1 – E2 + E3 = I1r1 + I2 r2 + I3r3 + I4r4.

Таким образом, получаем формулу второго закона Кирхгофа в комплексной форме:

Уравнение для постоянных напряжений – 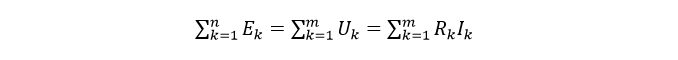Уравнение для переменных напряжени –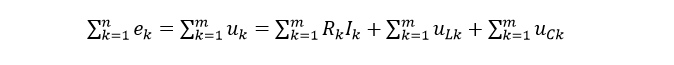

Теперь можем сформулировать определение 2 (второго) закона Кирхгофа:

Второй закон Кирхгофа гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура, равна алгебраической сумме ЭДС, входящих в этот контур. В случае отсутствия источников ЭДС, суммарное напряжение равно нулю.

Иначе формулируя второе правило Кирхгофа, можно сказать: при полном обходе контура потенциал, изменяясь, возвращается к начальному значению.

При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура, при этом падение напряжения на ветви считается положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, в противном случае – отрицательным.

Определить знак можно по алгоритму:

• 1. выбираем направление обхода контура (по или против часовой стрелки);
• 2. произвольно выбираем направления токов через элементы цепи;
• 3. расставляем знаки для напряжений и ЭДС по правилам (ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура со знаком «+», иначе – «-»; напряжения, падающие на элементах цепи, если ток, протекающий через эти элементы совпадает по направлению с обходом контура, со знаком «+», в противном случае – «-»).

Закон Ома является частным случаем второго правила для цепи.

Приведем пример применения второго правила Кирхгофа:

По данной электрической цепи (Рис 6) необходимо найти ее ток. Произвольно берем положительное направление тока. Выберем направление обхода по часовой стрелке, запишем уравнение 2 закона Кирхгофа:

Знак минус означает, что выбранное нами направление тока противоположно его действительному направлению.

Решение задач

1. По приведенной схеме записать законы Кирхгофа для цепи.

2. На рисунке приведена цепь с двумя источниками ЭДС величиной 12 В и 5 В, с внутренним сопротивлением источников 0,1 Ом, работающих на общую нагрузку 2 ома. Как будут распределены токи в этой цепи, какие они имеют значения?.

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

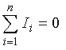
где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 – I2 + I3 – I4 + I5 = 0

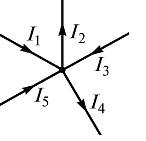
В этом уравнении токи, направленные к узлу, приняты положительными.

Физически первый закон Кирхгофа – это закон непрерывности электрического тока.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

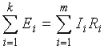
где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii , Ri – ток и сопротивление i -й ветви.

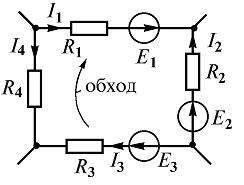
Так, для замкнутого контура схемы (рис. 2 ) Е1 – Е2 + Е3 = I1R1 – I2R2 + I3R3 – I4R4

Замечание о знаках полученного уравнения:

1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;

2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.

Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи.

Расчет разветвленной электрической цепи с помощью законов Кирхгофа

Метод законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.

Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b , следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.

Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только ( y – 1) уравнений являются независимыми друг от друга.

Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b – (y – 1) = b – y +1 .

Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.

Составим систему уравнений Кирхгофа для электрической цепи (рис. 3 ). Схема содержит четыре узла и шесть ветвей.

Поэтому по первому закону Кирхгофа составим y – 1 = 4 – 1 = 3 уравнения, а по второму b – y + 1 = 6 – 4 + 1 = 3 , также три уравнения.

Произвольно выберем положительные направления токов во всех ветвях (рис. 4 ). Направление обхода контуров выбираем по часовой стрелке.

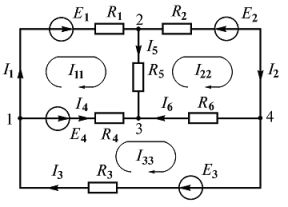
Составляем необходимое число уравнений по первому и второму законам Кирхгофа

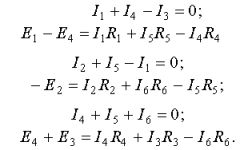
Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.
Потенциальная диаграмма – это графическое изображение второго закона Кирхгофа, которая применяется для проверки правильности расчетов в линейных резистивных цепях. Потенциальная диаграмма строится для контура без источников тока, причем потенциалы точек начала и конца диаграммы должны получиться одинаковыми.

Рассмотрим контур abcda схемы, изображенной на рис. 4. В ветке ab между резистором R1 и ЭДС E1 обозначим дополнительную точку k.

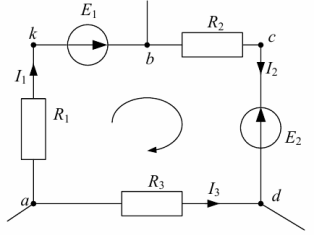
Рис. 4. Контур для построения потенциальной диаграммы

Потенциал любого узла принимаем равным нулю (например, ?а= 0), выбираем обход контура и определяем потенциалы точек контура: ?а = 0, ?к = ?а – I1R1 , ? b = ? к + Е1, ?с = ? b – I2R2 , ? d = ?c – Е2, ? a = ?d + I3R3 = 0

При построении потенциальной диаграммы необходимо учитывать, что сопротивление ЭДС равно нулю (рис. 5 ).

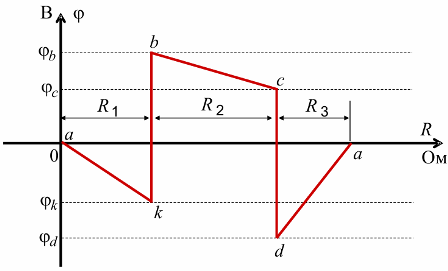
Рис. 5. Потенциальная диаграмма

Законы Кирхгофа в комплексной форме

Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.

Первый закон Кирхгофа : «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»

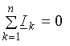
Второй закон Кирхгофа : «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».

Законы Кирхгофа (более корректно – правила Киргхгофа) применяются при расчете сложных (разветвленных) электрических цепей. Предлагаю рассмотреть их по очереди и начать, естественно, с первого.

Здесь:

• I i – ток в узле,
• n – число проводников, сходящихся в узле,
• токи, втекающие в узел ( I₁, In ) считаются положительными,
• вытекающие токи ( I₂, I₃ ) – отрицательными.

В таком виде этот закон звучит и выглядит, наверное, очень академично, поэтому предлагаю все несколько упростить.

Нарисуем разветвленную электрическую цепь в более привычном виде (рис.2) и дадим такую формулировку:

Сумма токов втекающих в узел равна сумме токов, вытекающих из узла.

Для этого случая формула первого закона Кирхгофа примет вид: I= I₁+I₂+. +In , что для повседневных вычислений гораздо удобнее.

ВТОРОЙ ЗАКОН КИРХГОФА

Второй закон Кирхгофа определяет зависимость между падениями напряжений и ЭДС в замкнутых контурах и имеет следующий вид (рис.3) и определение:

При отсутствии в контуре ЭДС сумма падений напряжений равна 0.

Теперь несколько пояснений по практическому применению этого правила Кирхгофа:

• поскольку, алгебраическая сумма требует учета знака следует выбрать направление обхода контура ( на рис.3 – по часовой стреклке), токи и напряжения, совпадающие с этим направлением считать положительными, иные – отрицательными. При затруднении в определении направления тока, возьмите произвольное, если в результате вычислений получите результат со знаком "-", поменяйте выбранное направление на противоположенное.
• для нашего примера можно записать:
  U₁+U₃-U₂=0
  U₄+U₅-U₃=0
• кроме того, руководствуясь первым правилом Кирхгофа :
  I_вх – I₁ – I₂ = 0
  I₁ – I₃ – I₄=0
  I₄ – I₅=0
  I₂ + I₃ + I₅ – I_вых=0 ,

получаем систему из 6 уравнений, полностью описывающую рассматриваемую электрическую цепь.

© 2012-2019 г. Все права защищены.

Все представленные на этом сайте материалы имеют исключительно информационный характер и не могут быть использованы в качестве руководящих и нормативных документов