Уравнение баланса мощностей в цепях синусоидального тока очевидно должно учитывать как мощность, необратимо преобразующуюся в другие виды энергии (активную мощность), так и мощность обратимых преобразований энергии (реактивную мощность). Поэтому уравнения баланса мощностей в цепях синусоидального тока выглядят следующим образом:
Сумма активных мощностей источников энергии равна сумме активных мощностей преемников энергии.
Алгебраическая сумма реактивных мощностей источников энергии равна алгебраической сумме реактивных мощностей преемников энергии. Реактивная мощность может быть положительной (индуктивный элемент) и отрицательной (емкостной элемент).
Пример 9
Составить уравнения баланса мощностей для цепи согласно условию примера 7 (рис.1.18).
Решение
Активная и реактивная мощности, отдаваемые источником энергии, нами найдены (см. пример 8) и так как источник энергии всего один, то:
(Вт);
(вар);
Напряжения и токи на всех участках цепи нами также найдены ранее (см. пример 7).
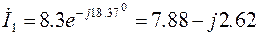(А);
(А),
(А),
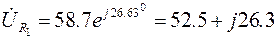(В),
(В),
(В),
(В),
(В).
Найдем комплексно сопряженные токи
(А);
(А);
(А).
Определим комплексные мощности на каждом из элементов заданной по условию цепи.
Комплексная мощность на резисторе R1:
;
(Вт); 
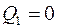(вар);
Комплексная мощность на резисторе R2:
;
(Вт); 
(вар);
Комплексная мощность на катушке индуктивности L:
;
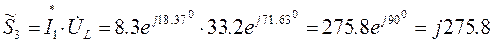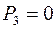(Вт); 
(вар);
Комплексная мощность на резисторе R3:
;
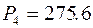(Вт); 
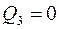(вар);
Комплексная мощность на конденсаторе С:
(Вт); 
(вар);
Определим сумму активных мощностей приемников.
(Вт);
Определим сумму реактивных мощностей приемников.
(вар).
Очевидно, что баланс активных и реактивных мощностей выполняется т.е.
(Вт);
(вар).
Задание
2.1 Начертить схему замещения электрической цепи с обозначением характера сопротивлений всех ветвей.
2.2 Указать на схеме условные положительные направления токов в ветвях. Определить токи всех ветвей в комплексной форме.
2.3 Определить показания приборов.
2.4 Построить векторную диаграмму токов и напряжений на комплексной плоскости.
2.5 Построить осциллограмму тока в ветви или напряжения на участке, определенном в задании.
2.6 Составить баланс активных и реактивных мощностей.
Исходные данные приведены в таблице 1. Номер схемы для расчётов выбирается из таблицы 1 исходных данных. Номер варианта выбирается согласно номеру по списку в журнале преподавателя.
Значения индуктивностей заданы в микрофарадах (мкФ), емкостей – в милигенри (мГн). Частота тока f = 50 (Гц).
Значения индуктивных и емкостных сопротивлений элементов окркуглять до целого числа.
При составлении баланса активных и реактивных мощностей погрешность вычислений оценить согласно формулам:
;
.
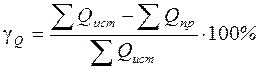Относительная погрешность не должна превышать 5%.
Уравнение баланса мощностей в цепях синусоидального тока очевидно должно учитывать как мощность, необратимо преобразующуюся в другие виды энергии (активную мощность), так и мощность обратимых преобразований энергии (реактивную мощность). Поэтому уравнения баланса мощностей в цепях синусоидального тока выглядят следующим образом:
Сумма активных мощностей источников энергии равна сумме активных мощностей преемников энергии.
Алгебраическая сумма реактивных мощностей источников энергии равна алгебраической сумме реактивных мощностей преемников энергии. Реактивная мощность может быть положительной (индуктивный элемент) и отрицательной (емкостной элемент).
Пример 9
Составить уравнения баланса мощностей для цепи согласно условию примера 7 (рис.1.18).
Решение
Активная и реактивная мощности, отдаваемые источником энергии, нами найдены (см. пример 8) и так как источник энергии всего один, то:
(Вт);
(вар);
Напряжения и токи на всех участках цепи нами также найдены ранее (см. пример 7).
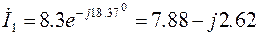(А);
(А),
(А),
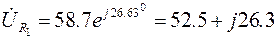(В),
(В),
(В),
(В),
(В).
Найдем комплексно сопряженные токи
(А);
(А);
(А).
Определим комплексные мощности на каждом из элементов заданной по условию цепи.
Комплексная мощность на резисторе R1:
;
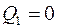(Вт); (вар);
Комплексная мощность на резисторе R2:
;
(Вт); (вар);
Комплексная мощность на катушке индуктивности L:
;
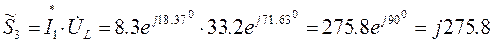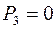(Вт); (вар);
Комплексная мощность на резисторе R3:
;
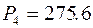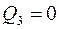(Вт); (вар);
Комплексная мощность на конденсаторе С:
(Вт); (вар);
Определим сумму активных мощностей приемников.
(Вт);
Определим сумму реактивных мощностей приемников.
(вар).
Очевидно, что баланс активных и реактивных мощностей выполняется т.е.
(Вт);
(вар).
Задание
2.1 Начертить схему замещения электрической цепи с обозначением характера сопротивлений всех ветвей.
2.2 Указать на схеме условные положительные направления токов в ветвях. Определить токи всех ветвей в комплексной форме.
2.3 Определить показания приборов.
2.4 Построить векторную диаграмму токов и напряжений на комплексной плоскости.
2.5 Построить осциллограмму тока в ветви или напряжения на участке, определенном в задании.
2.6 Составить баланс активных и реактивных мощностей.
Исходные данные приведены в таблице 1. Номер схемы для расчётов выбирается из таблицы 1 исходных данных. Номер варианта выбирается согласно номеру по списку в журнале преподавателя.
Значения индуктивностей заданы в микрофарадах (мкФ), емкостей – в милигенри (мГн). Частота тока f = 50 (Гц).
Значения индуктивных и емкостных сопротивлений элементов окркуглять до целого числа.
При составлении баланса активных и реактивных мощностей погрешность вычислений оценить согласно формулам:
;
.
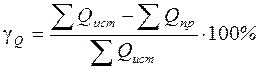Относительная погрешность не должна превышать 5%.
Комплексной мощностью цепи называют комплексное число S, модуль которого равен полной мощности S= UI цепи, а аргумент — углу сдвига фаз ф = х ?и – Ч / ( между током и напряжением на ее входе:
где /* = /с _/Т ‘ — комплексно-сопряженный ток.
Таким образом, комплексная мощность цепи равна произведению комплекса напряжения U на входной комплексно-сопряженный ток / .
Переходя от показательной формы записи S к тригонометрической S = ^соБф + у^ыпф, устанавливаем, что действительная часть комплексной мощности равна активной мощности цепи
Мнимая часть комплексной мощности S представляет собой реактивную мощность цепи
С учетом (2.79) и (2.80) выражение (2.78) можно записать следующим образом:
Следовательно, комплексная мощность S представляет собой комплексное число, действительная часть которого равна активной мощности цепи Р, а мнимая — реактивной Q, причем если перед символом у стоит знак «минус», то это реактивная емкостная мощностъ -Qc, а если знак «плюс» — реактивная индуктивная мощность +Ql.
Упражнение 2.7. Рассчитать полную, активную и реактивную мощности цепи, комплекс напряжения и комплекс тока на зажимах которой
Ц= Юс у ‘ 30 ° Ви/=2е" у ‘ 45 °А.
- 1. Комплексно-сопряженный ток / = 2e j45 А.
- 2. Комплексная мощность S = Щ* = Юе 730 • 2с 74э = 20e j15 В А.
- 3. Активная мощность P = Sco$>q> = 20cos75° = 5,2 Вт.
- 4. Реактивная мощность Q = Q, = .Ssincp = 20sin75° = 19,3 вар.
Баланс мощностей. Из закона сохранения энергии следует, что сумма мгновенных мощностей, отдаваемых всеми источниками цепи, должна быть равна сумме мгновенных мощностей, потребляемых всеми приемниками энергии:
где пит — число источников и приемников энергии в цепи.
Примечание. Заметим, что потребляется и отдается не мощность, а электрическая энергия.
Уравнение (2.82) называют уравнением (условием) баланса мощностей.
В цепях синусоидального тока рассматривают баланс комплексных, активных и реактивных мощностей.
Условием баланса комплексных мощностей является соотношение, аналогичное (2.82): 
Для практических расчетов условие баланса комплексных мощностей цепи представляют в следующем виде:
при этом слагаемые, стоящие в левой части (2.84), берут со знаком «плюс», если совпадают направления тока Ik и ЭДС Ек источника напряжения и не совпадает направление тока Jk с направлением напряжения Uk на зажимах источника тока. В противном случае эти слагаемые берут со знаком «минус».
Из условия баланса комплексных мощностей следуют условия баланса активных и реактивных мощностей:
• активная мощность, отдаваемая всеми источниками энергии, равна активной мощности всех ее потребителей (она полностью расходуется в резистивных элементах цепи):
• реактивная мощность всех источников равна реактивной мощности всех потребителей (она циркулирует между источниками энергии и ее потребителями):
где Rk и jXk = jXLk – jXCk — действительная и мнимая части комплексного сопротивления к-то пассивного элемента.
Упражнение 2.8. Для цепи (рис. 2.49) с параметрами Е = 10е у9 ° В, J = 2е
‘ Ы) А, /?, = R2 = /?3 = Хи = Хсз = ХС4 = 5 Ом рассчитать комплексы напряжений и токов ветвей. Правильность результатов расчета проверить посредством составления баланса мощностей.
1. Находим комплексы узловых Y<, и У22, межузловой Уп проводимостей и комплексы узловых токов и J22:
2. Воспользовавшись калькулятором ElCalc, определим комплексы узловых Un и Ц22 и межузлового Un напряжений:
3. Находим комплексы токов ветвей по закону Ома:
4. Комплексная мощность, отдаваемая источниками,
должна быть равна комплексной мощности, потребляемой приемниками:
Таким образом, условие баланса мощностей с допустимой погрешностью выполнено.
Задание 2.10. В цепи (рис. 2.50) с параметрами Е – 2 В, У = 4 мА, /?, = 1 кОм, R2 = 3 кОм, Xl = 2 кОм, Хс= 3,33 кОм известны комплексы токов и напряжений на элементах 
цепи:
Проверить условия баланса мощностей в цепи.
Запустить программу 2.10 (см. приложение 3) и занести с клавиатуры значения активных, реактивных и полных мощностей, отдаваемых источниками и потребляемых приемниками, в соответствующие поля таблицы.