Двоичная система счисления это в информатике

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов: 0 и 1. Двоичную цифру называют битом. Двоичная система счисления является основной системой представления информации в памяти компьютера.

Сложение, вычитание и умножение двоичных чисел.

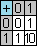
Пример: 1001 + 10 = 1011

Пример: 1111101 – 10001 = 1101100

Пример: 1111 · 1001 = 10000111

Перевод чисел.

Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.

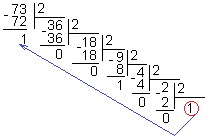
Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания двоичной системы счисления на соответствующие цифры в разрядах двоичного числа.

Пример: требуется перевести двоичное число 10110110 в десятичное. В этом числе 8 цифр и 8 разрядов ( разряды считаются, начиная с нулевого, которому соответствует младший бит). Представим его в виде суммы степеней с основанием 2: 10110110₂ = (1·2 7 )+(0·2 6 )+(1·2 5 )+(1·2 4 )+(0·2 3 )+(1·2 2 )+(1·2 1 )+(0·2 0 ) = 128+32+16+4+2 = 182₁₀

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.

Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 10 3 + 4 * 10 2 + 7 * 10 1 + 6 * 10 0

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 – это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.

Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 1*2 2 + 0*2 1 + 1*2 0 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

Тема: «Двоичная система счисления».

Цел урока:

• обобщить и закрепить знания об основных понятиях позиционных систем счисления на примере двоичной системы счисления;
• активизировать познавательную деятельность учащихся;
• показать применение игровых ситуаций на уроке;

1. Повторение и обобщение предыдущих знаний.

Повторение учащимися основных понятий позиционных систем счисления может быть организовано в виде игры по принципу «домино» (карточка делится пополам на вопрос-ответ, разрезаются и раздаются, дети ищут ответ на вопрос, образуя при этом пару для дальнейшей работы). Можно предложить следующие определения для контроля.

Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).

Количество цифр, используемых в системе счисления для записи чисел, называется ее основанием.

Существуют позиционные и непозиционные системы счисления.

Непозиционной системой счисления называется система, в которой вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа.

Позиционной системой счисления называется система, в которой вес каждой цифры измеряется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.

Поскольку за основание системы счисления можно принять любое натуральное число, то существует бесчисленное множество позиционных систем счисления. Рассмотрим традиционные из них.

2. Мотивация рассмотрения двоичной системы счисления

Учитель. Люди предпочитают десятичную систему счисления вероятно потому, что с древних времен они считали по пальцам, а пальцев у людей по 10 на руках и ногах.

Десятичная система счисления пришла к нам из Индии.

Но не всегда и везде используют десятичную систему счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.

Для общения с ЭВМ используют, кроме десятичной, двоичную, восьмеричную и шестнадцатеричную системы счисления.

• Какие же цифры используют в двоичной системе счисления (восьмеричной, шестнадцатеричной) системе счисления?
• Как формируется натуральный ряд?
• Как записываются и читаются числа, и какие разряды чисел существуют в двоичной системе счисления?

Все это мы узнаем с вами на уроке, а помощницей нам будет известная десятичная система счисления.

Из всех систем счисления особенно проста и поэтому интересна для технической реализации в ЭВМ двоичная система счисления.

В ЭВМ используют двоичную систему, потому что она имеет ряд преимуществ перед другими системами:

• для ее реализации нужны технические элементы с двумя возможными состояниями (есть ток, нет тока; включено, выключено и т.д. Одному из состояний ставится в соответствие 1, другому – 0), а не десять, как в десятичной системе,
• представление информации посредством только двух состояний надежно и помехоустойчиво,
• упрощается выполнение арифметических действий,
• возможность использовать аппарат булевой алгебры для выполнения логической преобразований информации

Используя знания предыдущего урока заполним следующую таблицу «Сведения о двоичной системе» .

При заполнении таблицы учащиеся ориентируются на знания десятичной системы счисления и знания предыдущего урока. Каждый этап таблицы дополняется и разъясняется учителем, делаются выводы.

3. Попробуем составить таблицу первых 10 двоичных чисел.

Учитель: Сколько потребуется разрядов для записи цифры десятичного числа?

Ученики вычисляют: 2 3 = 8, 2 4 = 16. Значит для записи цифры десятичного числа достаточно 4 разрядов.

Учитель: составим таблицу первых десятичных чисел

При наличии времени (и более сильным учащимся) можно предложить продолжить данную таблицу, формируя натуральный ряд чисел двоичной системы счисления.

Вывод: недостаток двоичной системы – это быстрый рост числа разрядов, необходимых для записи чисел.

Учитель: оказывается, что мы с вами повторили открытие одного немецкого ученого математика Вильгельм Готфрид Лейбниц (1646-1716)

Медаль, нарисованная В.Г Лейбницем, поясняет соотношение между двоичной и десятичной системами счисления.

Начиная со студенческих лет и до конца жизни великий европеец, немецкий ученый Вильгельм Готфрид Лейбниц (1646-1716), занимался исследованием свойств двоичной системы счисления, ставшей в дальнейшем основной при создании компьютеров. Он придавал ей некий мистический смысл и считал, что на ее базе можно создать универсальный язык для объяснения явлений мира и использования во всех науках, в том числе в философии. Сохранилось изображение медали, нарисованное В. Лейбницем в 1697 г., поясняющее соотношение между двоичной и десятичной системами исчисления:

На ней была изображена табличка из двух столбцов, в одном числа от 0 до 17 в десятичной системе, а в другом – те же числа в двоичной системе счисления. Вверху была надпись: «2,3,4,5 и т.д. Для получения их всех из нуля достаточно единицы». Внизу же гласила надпись: «Картина создания. Изобрёл ГГЛ. МDС XCYII».

Учитель: постарались вы на славу, предлагаю отдохнуть. Выполним зарядку для рук. Будем показывать числа, которые мы только что перевели в двоичную систему счисления.

Если 0- загибаем палец, если 1 – оттопыриваем. Учитель сначала последовательно, затем в разбивку говорит числа в десятичной системе счисления, а учащиеся показывают их в двоичной системе на пальцах, и наоборот. Данное упражнение вносит эмоциональный характер, но требует внимания от учащихся.

5. Демонстрация решения задачи, связанной с переводом десятичного числа в двоичную систему счисления пальцевым методом.

Смысл перевода прост: нумеруем на одной руке (левой, ладонь к себе)от мизинца до большого пальца разряды от 0 до 4, что соответствует числам в десятичной системе 1,2, 4, 8,16. Считая, что 0- это согнутый палец, а 1 – оттопыренный, при решении задач, связанных с переводом целых чисел в двоичную из десятичной системы счисления требуется лишь сложить эти цифры, соответствующие загнутым пальцам. Данное упражнение, основанное на самом древнем способе- счете на пальцах, подразумевает развёрнутую форму записи числа в двоичной системе счисления. (Две руки можно использовать для перевода целых чисел до 512, так и для перевода дробных конечных чисел, где левая рука – целая часть числа, а правая – дробная). Учитель говорит число в десятичной системе (до 31 или 62), а школьники устно переводят число на пальцах в двоичную систему и записывают ответ. Для больших чисел приводится сам развёрнутый способ перевода числа из двоичной системы счисления в десятичную с примером.

6. Затем учитель говорит, что существует и обратный способ перевода, предлагая алгоритм перевода десятичного целого числа в двоичную систему счисления.

Приводятся примеры. Сложность перевода для детей в том, что правило деления отличается от математического тем, что при делении чисел требуется определить частное сразу, а не поразрядно. Каждый этап комментируется учителем

Перевести 23₁₀ в двоичную систему.

7. Решение упражнений

Затем предлагается самостоятельно перевести числа из десятичной системы в двоичную .

Например, перевести числа 18; 36; 47; 235 и др. из десятичной системы счисления в двоичную систему с помощью алгоритма (с записью в тетрадях).

8. Подведение итогов и задание на дом.

Для общения с компьютером нужна двоичная (восьмеричная, шестнадцатеричная) система счисления. В каких (кроме компьютера) приборах (и не только) применяется двоичная система счисления? Оправдано ли это применение (приведите аргументы в защиту).

Возможный ответ: http://www.compulenta.ru

Время в двоичной системе.

В Японии поступили в продажу необычные электронные часы, отображающие время в двоичной системе счисления. Выглядят часы также довольно необычно. Они заключены в круглый металлический корпус, однако вместо циферблата со стрелками или индикатора с цифрами под стеклом находится печатная плата зеленого цвета с резисторами, конденсаторами и расположенными в два ряда десятью светодиодами. Именно они и показывают время. Каждый из светодиодов соответствует двоичному разряду.В верхнем ряду имеются четыре диода, соответствующих числам от одного (20) до восьми (23) и показывающих часы. Нижний ряд из шести светодиодов (разряды от 1 до 32) показывает минуты. Чтобы получить нужное значение нужно сложить числа, соответствующие горящим светодиодам. Для удобства владельца рядом со светодиодами указаны числа, которым те соответствуют. Цена часов составляет 8900 иен или около 80 долларов США.