Двоичная система счисления объяснение

Когда в древности люди только изобретали счёт, они, как сейчас маленькие дети, считали на пальцах. Пальцев на руках – десять, поэтому и система счисления у нас – десятичная. Однако наша система счёта компьютеру не слишком-то понятна: ему ближе двоичная. У компьютера нет десяти пальцев, но, с другой стороны, и двух тоже нет. Откуда тогда взялась двоичная система, что это за ноль и единица, которыми думает компьютер? И как из них получаются обычные, понятные цифры?

Для того чтобы в общих чертах понять, как думает компьютер, начнём с самого начала. Компьютер, по сути, – это много всякой электроники, собранной вместе в правильном порядке. А электроника (до того, как к ней добавили программу) понимает только одно: включена она или выключена, есть сигнал или нет сигнала.

Обычно «есть сигнал» обозначают единицей, а «нет сигнала» – нулём: отсюда и выражение, что «компьютер говорит на языке нулей и единиц».

Этот язык нулей и единиц называют ещё двоичной системой счисления – потому что в ней всего две цифры. Наша привычная система счисления – десятичная, в ней десять цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Но есть и множество других – восьмеричная, пятеричная, одиннадцатиричная и какая угодно ещё.

У нас с вами нет цифры «десять», правда? Число 10 состоит из двух цифр – 1 и 0.

Точно так же в пятеричной системе счисления не будет цифры «5», только 0, 1, 2, 3 и 4.

Посчитаем в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34, 40, 41, 42, 43, 44, 100 (. ), 101, 102 и так далее. Можно сказать, что как система счисления называется, такой цифры в ней и нет. В нашей десятичной нет цифры «10», в пятеричной нет цифры «5» (и всех, которые после неё), в восьмеричной – «8» и так далее.

А в шестнадцатиричной «16», например, есть! Поэтому нам шестнадцатиричную систему понять ещё сложнее. Давайте посчитаем в шестнадцатиричной:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, 22…97, 98, 99, 9A, 9B, 9C, 9D, 9E, 9F, A0, A1, A2… F7, F8, F9, FA, FB, FC, FD, FE, FF, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 10A, 10B, 10C и так далее.

Двоичная система счисления, впрочем, тоже выглядит странновато для непривычного взгляда:

0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001…

Вот примерно такими числами и думает компьютер где-то внутри себя. Но человеку такими числами думать совершенно неудобно, поэтому мы преобразуем числа из двоичной в более удобную систему счисления.

В компьютерных программах часто используют восьмеричную и шестнадцатиричную системы: компьютеру легко их понять (потому что 8=2*2*2, 16=2*2*2*2, а с двоичной системой компьютер знаком изначально), а для людей это удобно, потому что поближе к привычной десятичной.

Как же переводить числа из одной системы счисления в другую? Чтобы понять принцип, будем, как мы с вами любим, разбираться на конфетах.

И на конфетах мы с вами будем переводить число 33 в восьмеричную систему счисления. Мы решим, что единицы – это сами конфеты, а десятки – это коробки, в каждой из которых лежит по десять конфет. Вот и получится, что 33 – это 3 коробки по 10 конфет и ещё 3 конфеты где-то сбоку.

Но мы переводим наше конфетное богатство в восьмеричную систему счисления, а это значит, что нам надо вытряхнуть все конфеты из коробочек по 10, сложить в коробочки по 8 и посмотреть, что из этого выйдет.

Из 33 получится 4 полных восьмеричных коробочки и 1 конфета останется сама по себе, так как 33/8=4 (ост. 1). То есть 33=8*4+1 – так в восьмеричной системе счисления получается число 41.

33 в десятичной – это 41 в восьмеричной. Это одно и то же число, просто разложенное по разным коробочкам, переведённое в разное основание. Количество конфет не поменялось, мы просто считали их по-разному!

Двоичная система, как мы уже выяснили, более странная и непривычная для человеческого взгляда. Давайте попробуем перевести 33 в двоичную – получится аж 16 коробочек по 2! И что же делать? Писать 16 как-то странно, помня о том, что в двоичной системе есть только ноль и единица, а шестёрки, которая нам нужна для шестнадцати, совершенно точно нет!

Посмотрим на нашу десятичную систему. В ней мы считаем десятки – 10, 20, 30, 40, 50, 60, 70, 80, 90 – а когда у нас набирается десять десятков, мы достаём большую коробку – 100.

У нас 100 – это 10*10, 1000 – 10*10*10, 10 000 – 10*10*10*10 и так далее. Для других систем счисления это работает точно так же! В восьмеричной системе 100=8*8, 1000=8*8*8; в двоичной 100=2*2, а 1000=2*2*2; а в шестнадцатиричной (есть и такая, помните?) 100=16*16, 1000=16*16*16.

Здесь нам пригодятся степени. Если вы их ещё не проходили в школе, не пугайтесь, степени – это очень просто. Число в степени – это число, сколько-то раз умноженное на само себя. То есть 5 3 =5*5*5 (пять в третьей степени – это пять, три раза умноженная сама на себя: 5*5*5), или 8 5 =8*8*8*8*8 (восемь в пятой степени – это восемь, пять раз умноженная на саму себя: 8*8*8*8*8).

Если мы вспомним про наши 10 000=10*10*10*10 в десятичной и 1000=8*8*8 в восьмеричной, то можно легко заметить, что сколько нулей, столько раз и умножаем на само себя. Другими словами, количество символов в числе минус один – это степень, в которую надо возвести основание. В числе 1000 у нас четыре символа, значит умножать надо 4–1, то есть 3 раза. Если основание 10, то тысяча – это 10, три раза умноженная сама на себя: 10*10*10. Если основание 8, то тысяча – это 8, три раза умноженная сама на себя: 8*8*8.

Обо всём этом мы заговорили, пытаясь перевести 33 в двоичную систему. Просто так поделить это число на коробочки по 2 оказалось затруднительным. Но если вспомнить про наши сотни-тысячи, можно задуматься: а ведь в двоичной 100=2*2, 1000=2*2*2, 10 000=2*2*2*2 и так далее.

Для перевода из десятичной системы в двоичную удобно помнить степени двойки. Даже можно сказать, что без этой хитрости со степенями мы устанем, умаемся и немножко сойдем с ума. А степени двойки выглядят как-то так:

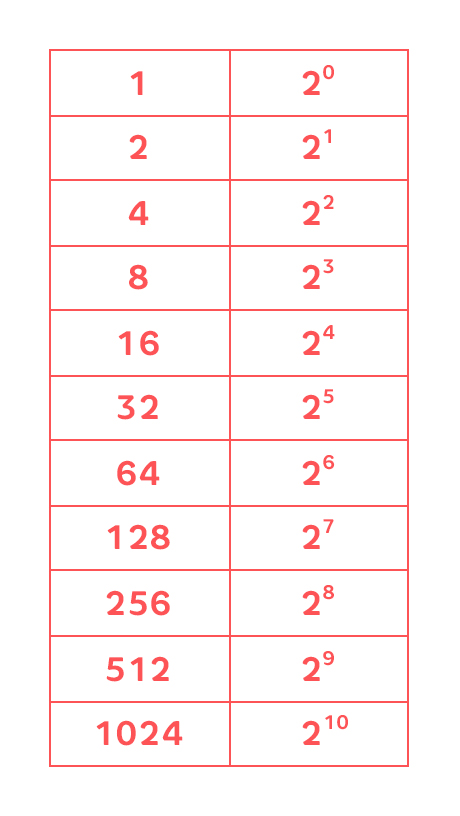
Теперь, глядя на табличку, мы видим, что 33=2 5 +1, то есть 33=2*2*2*2*2+1. Вспоминаем – сколько раз умножаем, столько будет нулей – то есть наше 2*2*2*2*2 в двоичной системе будет 100000. Не забудем оставшуюся в стороне единичку, и получится, что 33 в десятичной – это 100001 в двоичной. Правильно и красиво это записывают так:

Давайте (чтобы совсем хорошо понять) переведём в двоичную систему число 15.

1. В первую очередь – смотрим в табличку.

а) Какое самое близкое к 15 число в ней? Нет, 16 не подходит, оно больше, а нам нужно самое близкое, которое меньше. Получается, что это 8, то есть 2 3 , то есть 2*2*2.

б) Восемь конфет из 15 разобрали, осталось – 15-8 – семь. Какое ближайшее число из таблички? Нет, восемь снова не подойдет, см. выше. Подойдет четыре, то есть 2 2 , то есть 2*2.

в) Четыре из семи конфет разобрали, осталось – 7-4 – три. Из таблички понимаем, что самое близкое число – 2, то есть 2 1 , то есть просто 2.

г) Три минус два – осталась 1 конфета, тут уже табличка не понадобится. В таблички такого рода можно не смотреть, когда ваш остаток меньше основания, а наша единица точно меньше двойки.

1. Собираем всё найденное в табличке вместе: 15=2 3 + 2 2 + 2 1 + 1, оно же: 15=2*2*2 + 2*2 + 2 + 1.
2. В двоичной системе 2*2*2=1000, 2*2=100, 2=10, помните? И у нас получается 1000+100+10+1, то есть 1111.
3. Итак,

Когда просто смотришь на все эти шаги, кажется, что это просто свалка из Кучи Разных Странно Написанных Цифр. И запутаться во всём этом в первый раз – нормально. И во второй, и в третий. Просто попробуйте сделать это ещё и ещё раз – по шагам, как написано выше, и всё получится.

И наоборот это тоже работает! Например, число 11010101₂ – как из него сделать понятное десятичное? Точно так же, при помощи таблички. Пойдем с конца:

1*2 0 +0*2 1 +1*2 2 +0*2 3 +1*2 4 +0*2 5 +1*2 6 +1*2 7 =

Вот примерно так компьютер понимает привычные нам числа.

Когда смотришь на это в первый раз, кажется, что это, во-первых, совершенно непостижимо, а, во-вторых, вообще не сработает. Поэтому сейчас мы с вами сделаем немножко математической магии, чтобы убедиться, что системы счисления – это такая же реальная вещь, как, например, задача «раздать пятерым детям пятнадцать печенек поровну».

Итак, возьмем пример 15+6 и решим его в разных системах счисления. Понятно, что в нашей, десятичной, получится 21. А что выйдет, например, в восьмеричной?

Переводим 15 в восьмеричную систему счисления. Первый шаг у нас при переводе в другую систему – посмотреть в табличку степеней. 8 2 – это уже 64, и в 15 оно точно уже никак не влезет, поэтому берем 8 1 – то есть просто 8. 15–8=7, оно меньше нашего основания 8, поэтому с ним мы ничего не делаем.

Итак, получилось, что 15=8 1 +7.

В восьмеричной системе логика точно такая же, как, например, в двоичной: 8 3 – это 1000, 8 2 – это 100, 8 1 – это 10. Получилось, что:

Напомню, наш пример был 15+6. 15 мы перевели в восьмеричную систему, как же перевести 6? Она меньше 8, нашего основания, поэтому ответ – оставить как есть. Наш пример сейчас выглядит так:

Теперь мы будем складывать в восьмеричной системе счисления. Как это делается? Так же, как и в десятичной, но надо помнить, что десяток в восьмеричной системе – это восемь, а не десять, и что 8 и 9 в ней не существует.

Когда мы считаем в десятичной системе, по сути, мы делаем так:

15+6=15+5+1=20+1=21

Попробуем проделать тот же фокус в восьмеричной системе:

Почему 17+1? Потому что 7+1=8, а 8 – это наш десяток! В восьмеричной системе 7+1=10, а значит, 17+1=20. Если на этом месте ваш мозг начинает бить тревогу и рассказывать, что здесь что-то не так, вернитесь в начало статьи, где мы с вами считали в разных системах счисления.

Теперь наш пример выглядит как

Переведем 25₈ обратно в нашу систему счисления. В десятичной мы бы, увидев число 25, могли сказать, что в нём две десятки и пять единиц. В восьмеричной, как вы, наверное, уже догадались, число 25₈ – это две восьмерки и пять единиц. То есть 25₈=2*8+5=21₁₀.

Итак, наш пример целиком:

Получилось точно такое же 21, какое вышло у нас в самом начале, когда мы посчитали 15+6 привычным нам способом в десятичной системе.

Арифметические правила не меняются от того, что мы выбрали другую систему счисления.

Поэтому и компьютер, переводя всё в нули и единицы, которые для нас выглядят непонятно и бессмысленно, не теряет при этом информацию, которую мы ему дали, и может, посчитав в удобной ему форме, выдать результат, переведя его обратно в привычный нам вид.

Здравствуйте, Хабровцы.
Пост можно было бы назвать: «Для любителей посчитать на пальцах», но это мы узнаем дальше.

Вступление: А что-же тянуть. Все что будет дальше, пойдет на тему подсчета в двоичной системе на пальцах. Кто еще не знает, постараюсь обьяснить, что это, как и зачем это осваивать.
Начну, пожалуй, с преимуществ:
1. Удобно переводить любое число с десятичной в двоичную системы и наоборот, не используя калькулятор.
2. Развивается моторика пальцев.
3. Развивается визуальное восприятие двоичных чисел.
Минусы:
1. Немного тренировки.
2. Нельзя в публичных местах показывать числа 26,27,352,378 и 891.

Суть:
Многим, наверняка, приходилось переводить между системами. И я думаю многие запомнили, что:
2-10
3-11
4-100
5-101
и т.д.
Логично, что исходя из того что каждая разрядность имеет два состояния, мы можем изобразить это дело на пальцах.
Поставьте перед собой руку (ладонью к себе), согните большой палец. Вот и есть единица. Разогните большой и согните указательный, вот и два. Тоесть разогнутый палец — это 0, а согнутый — 1. Так как начальные нули отбросились, мы имеем отсчет от «самой левой» единицы.
Названия пальцев — те которые загнуты:
средний, большой — 101 — 5
безымянный, средний -1100 — 12
мизинец, средний — 10100 — 20
Чтобы загибать мизинец, понадобиться некоторая практика. Но суть в другом. Представим разрядность каждого пальца руки, как 2^n (на фото)

То есть,

Теперь, представим, что нам нужно перевести число 25 в двоичную. Загибаем Мизинец — 16, Безымянный — 8 и большой — 1. т.к. 16+8+1=25.

Если не поняли, то вот еще пример, число 14, думаем: Мизинец — это много, средний нормально, но можно взять больше, поэтому — загибаем безымянный, это 8. Запомнили, далее средний — +4, єто уже 12 и указательный — +2, итог 14.

Так же поступаем с двоичными. Вот например видим где-то: 1011101. Представляем это на руках с разрядностями (уже две руки).

64+16+8+4+1=93
Имеем: 1011101(2) = 93(10)

Заключение: Таким образом мы можем использовать данный метод от 0 до 1023, используя пальцы и обладая элементарной арифметикой. Но при добавлении, хотя бы, одного разряда, можно будет считать до 2047, и далее до 4095, 8191 и т.д. А это могут быть руки, ноги, веки, либо что-то еще что может иметь два состояния 1 и 0.

Скачать:

Предварительный просмотр:

Двоичная система счисления для младших классов

Цифры десятичной системы: 0, 1,2,…9

В двоичной системе всего 2 цифры: 0, 1

Заполняем пока только первый столбец таблицы известными цифрами десятичной системы.

10 в десятичной системе (когда закончились цифры) записывается как комбинация 1 и 0.

Каждое следующее число получается прибавлением 1 к предыдущему числу, согласно закону сложения в позиционных системах, который дети уже хорошо знают.

Для записи количества 2 в двоичной системе поступают также, как в десятичной, когда цифры закончились – записывают 2 как комбинацию 1 и 0.

Арифметика двоичной системы выглядит так:

0+0=0; 0+1=1; 1+0=1; 1+1=10

Используя эти правила каждое следующее число двоичной системы, получаем прибавлением 1 к следующему числу:

10 11 100 101 110 111 1001 1010

+ 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

11 100 101 110 111 1000 1010 1011

Записываем эти значения во второй столбец таблицы, по мере их получения.

Выясняем закономерность получения чисел 2,4,8,16: каждое число в двоичной системе получается добавлением нуля справа.