Единица измерения индуктивности контура

Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф

B), индукция пропорциональна силе тока в проводнике
(B

I), следовательно магнитный поток пропорционален силе тока (Ф

ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника
(размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.

Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.

Индуктивность – физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 Ампер за 1 секунду.

Также индуктивность можно рассчитать по формуле:

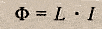
где Ф – магнитный поток через контур, I – сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды

Индуктивность взаимная – величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура , то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2).

Магнитный поток Ф₁₂ через контур 2, созданный током I₁ в контуре 1, прямо пропорционален току:

Коэффициент пропорциональности M₁₂ зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ И. в. измеряется в Генри.

Трансформаторная ЭДС. Принцип действия трансформатора основан на явлении электромагнитной индукции. Линии индукции магнитного поля, создаваемого переменным током в первичной обмотке, благодаря наличию сердечника практически без потерь пронизывают витки вторичной обмотки. Поскольку магнитный поток во вторичной обмотке изменяется со временем (т.к. в первичной обмотке переменный ток), то согласно закону Фарадея в ней возбуждается ЭДС индукции. Трансформатор может работать только на переменном токе, т.к. магнитный поток, созданный постоянным током, не изменяется с течением времени.

Пусть первичная обмотка трансформатора подключена к источнику тока с переменной ЭДС E₁ и с действующим значением напряжения U₁. На вторичной обмотке ЭДС E₂ и напряжение U₂.

Из законов Ома 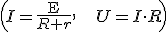следует, что напряжение на обмотке равно

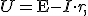(1)

где r — сопротивление обмотки. При изготовлении трансформатора сопротивление первичной обмотки r₁ делают очень малым, поэтому часто им можно пренебречь. Тогда

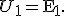
Если пренебречь потерями магнитного потока в сердечнике, то в каждом витке вторичной обмотки будет индуцироваться точно такая же ЭДС индукции e₁, как и ЭДС индукции e₂ в каждом витке первичной обмотки, т.е. e₁ = e₂. Следовательно, отношение ЭДС в первичной E₁ и вторичной E₂ обмотках равно отношению числа витков в них:

(2)

Трансформаторный ток. Токи обмоток обратно пропорциональны числам витков (I₁/I₂ приблиз = w₁/w₂ = 1/n). С увеличением тока активно-индуктивного приемника вторичное напряжение несколько снижается.

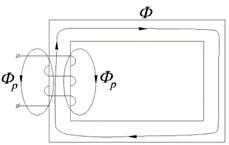
Рис.1.11. К определению магнитного потока рассеяния в катушке с ферромагнитным сердечником

часть магнитного потока катушки замыкается не по сердечнику, а по воздуху. Эта часть потока носит название потока рассеивания Ф_р (рис. 1.11). Таким образом, полный поток, сцепленный с витками катушки равен

На основании закона Ома для магнитной цепи (1.7) можно написать выражение для потока рассеяния:

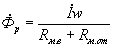Так как 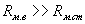, то .То есть поток рассеяния 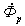, в отличие от потока в сердечнике, совпадает по фазе с током и связан с ним линейной зависимостью. Следовательно, на векторной диаграмме вектор потока будет совпадать с вектором тока (рис.1.12).

Рис.1.12. Векторная диаграмма магнитных потоков, ЭДС и токов катушки с ферромагнитным сердечником

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10620 – | 7341 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Индуктивность контура — это коэффициент пропорциональности между постоянным током, текущим в заданном замкнутом контуре, и потоком вектора магнитной индукции, создаваемым этим током через поверхность, окружённой этим контуром. Обозначение — , размерность — Гн (генри). Формульно:

• где

• Ф — поток вектора магнитной индукции,
• — индуктивность контура,
• — сила тока в контуре.

В большинстве задач данный параметр задан в условии, однако есть одна система, в которой данный параметр является расчётным. Это соленоид (рис. 1). Соленоидом называется провод, согнутый в виде спирали (он же, в принципе, катушка индуктивности). Формульно:

• где

• — индуктивность соленоида,
• — относительная магнитная проницаемость среды (табличные данные),
• м*кг* * ,
• — число витков,
• — площадь поперечного сечения витка,
• — длинна катушки.

Немного о — относительной магнитной проницаемости среды. Чаще всего в школьных задачах соленоид пустотелый, т.е. внутри него (витков) воздух, тогда . Иногда в него помещают сердечник, т.е. болванку формой повторяющую внутреннюю геометрию соленоида, тогда 1" title="displaystyle mu >1" > и по веществу, из которого состоит сердечник, можно в таблицах найти значение магнитной проницаемости.

Для ряда задач существует всё тот же вопрос о параллельном и последовательном соединении индуктивностей. Будем считать, что взаимной индукции нет (т.е. один контур экранирован от второго). Тогда:

• при параллельном подключении:

• где

• — общая индуктивность системы контуров,
• — сумма обратных индуктивностей, входящих в цепь.

В случае двух элементов, соединённых параллельно:

• при последовательном подключении:

• где

• — общая индуктивность системы контуров,
• — сумма индуктивностей, входящих в цепь.

Индуктивность — это физическая величина, характеризующая магнитные свойства электрической цепи. В некоторых источниках её называют коэффициентом самоиндукции, так как она зависит от текущего в замкнутом контуре тока и создаваемого им магнитного потока. Для определения величины этого показателя применяют несколько вариантов расчёта, которые основываются на различных физических параметрах.

Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

1. Величина параметра никогда не может быть меньше нуля.
2. Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

Способы расчёта

Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.

Через силу тока

Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:

• L — индуктивность контура (в генри);
• Ф — величина магнитного потока, измеряемого в веберах;
• I — сила тока в катушке (в амперах).

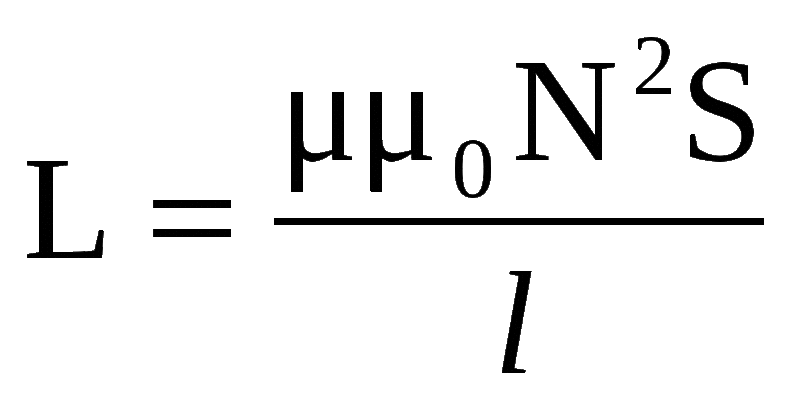
Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.

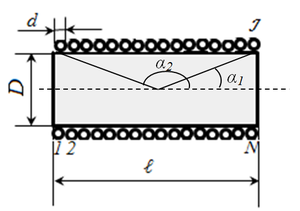
Соленоид конечной длины

Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:

• µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
• N — количество витков в катушке;
• S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
• l — длина соленоида в метрах.

Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:

• W — энергия магнитного потока, измеряемая в джоулях;
• I — сила тока в амперах.

Катушка с тороидальным сердечником

В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:

• N — число витков катушки;
• µ — относительная магнитная проницаемость;
• µ0 — магнитная постоянная;
• S — площадь сечения сердечника;
• π — математическая постоянная, равная 3,14;
• r — средний радиус тора.

Длинный проводник

Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:

• l — длина проводника в метрах;
• r — радиус сечения провода, измеряемый в метрах;
• µ0 — магнитная постоянная;
• µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
• µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
• π — число Пи;
• ln — обозначение логарифма.

Варианты измерения

Индуктивность катушки в физике определяется путём выполнения вычислений. Однако эту величину можно не только рассчитать, но и измерить. Делается это при помощи прямого или косвенного метода.

Прямой метод

Для измерения индуктивности катушки этим методом необходимо использовать специальные мостовые или прямопоказывающие устройства. С их помощью можно получить максимально точные данные, которые помогут выбрать требуемую катушку для схемы.

Порядок проведения измерений включает в себя следующие этапы:

1. К прямопоказывающему приспособлению подключают катушку.
2. После этого постепенно изменяют диапазоны измерений. Это делается до тех пор, пока получаемый результат не будет находиться примерно в середине интервала.
3. Полученный результат фиксируют и высчитывают с учётом цены деления прибора, а также коэффициента, соответствующего положению переключателя.

Прямой метод измерения можно применить и при определении индуктивности с помощью мостового приспособления. Оно имеет более точную шкалу, поэтому позволяет получить достоверные данные.

Измерение выполняют путём проведения таких действий:

1. Включённый мостовой прибор подсоединяют к катушке, индуктивность которой необходимо определить.
2. Аналогично прямопоказывающему устройству проводят переключение интервалов измерений.
3. После каждого такого действия ручку регулятора балансировки моста поочерёдно перемещают в одно и другое предельное положение.
4. Как только удалось определить диапазон, в котором мост будет сбалансирован, можно выполнять дальнейшие действия.
5. На следующем этапе измерений выполняется постепенное перемещение стрелочного индикатора.
6. После того как в динамике прибора исчезнет звук, необходимо зафиксировать показатели.
7. Затем их рассчитывают в соответствии с ценой деления шкалы и предусмотренным коэффициентом.

Косвенное определение

Для того чтобы измерить коэффициент самоиндукции, необходимо провести несколько подготовительных мероприятий. В первую очередь нужно собрать измерительную цепь по стандартной схеме, а также подготовить все необходимые приспособления (генератор синусоидального напряжения, частотомер, а также миллиамперметр и вольтметр, рассчитанные на переменный ток).

Порядок определения параметра:

1. К выходу генератора параллельно подключают вольтметр. Он должен быть переключён в режим, при котором верхнее предельное значение будет соответствовать напряжению в 3−5 вольт.
2. Аналогично подсоединяют и частотомер.
3. Отдельно собирают вторую цепь. В ней последовательно соединяют миллиамперметр и катушку, индуктивность которой нужно определить.
4. Затем обе цепи подключают параллельно друг к другу.
5. Подключённый генератор устанавливают в режим выработки синусоидального напряжения.
6. Путём изменения частоты добиваются такой работы приборов, при которой вольтметр будет показывать примерно 2 вольта. При этом сила тока на миллиамперметре будет постепенно уменьшаться.
7. После этого ручку частотомера перемещают в положение, соответствующее частоте измерений.
8. Как только эти действия будут выполнены, можно фиксировать значения.

Полученные данные переводятся в СИ, а затем выполняются все необходимые расчёты. Первым делом определяется индуктивное сопротивление. Для этого значения приборов подставляются в следующую зависимость: X=U/I, где U — напряжение, а I — сила тока. Результат расчётов будет выражен в омах.

После этого вычисляется индуктивность по формуле L=X/2 πF. В ней используются такие условные обозначения:

• X — индуктивное сопротивление;
• π — математическая постоянная (примерно 3,14);
• F — частота в герцах, при которой проводились измерения.

Индуктивность — это важный физический параметр, позволяющий определить магнитные свойства электроцепи. При точном его измерении и правильном проведении предусмотренных расчётов можно получить достоверные данные, которые понадобятся при выборе катушки.
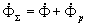