Анализ электрических цепей, в которых действуют сигналы любой формы, можно свести к анализу цепей с синусоидальными воздействиями. Поэтому изначально рассмотрим все особенности расчета цепей, относящиеся к синусоидальным токам и напряжениям, а затем обобщим их на цепи с другими видами воздействия.
Рассмотрим основные понятия, характеризующие переменный синусоидальный ток. Синусоидальный ток является периодическим. Пусть ток изменяется по закону синусов 
. График этой функции показан на рис. 4.3.
Дадим определение основным параметрам синусоидального тока.
Мгновенное значение – это значение тока в данный момент времени. Мгновенное значение меняется от точки к точке и обозначается строчной буквой i. Например, в момент времени t1мгновенное значение будет i1, в момент времени t2мгновенное значение будет i2.
 |
Мгновенные значения переменного тока в течение одной половины периода положительны, а в другие полпериода отрицательны. Одно из двух возможных направлений тока в проводнике принимается условно за положительное направление, этому направлению соответствуют положительные мгновенные значения. И наоборот, другому направлению тока в проводнике будут соответствовать отрицательные мгновенные значения.
Введение понятия положительных направлений токов, ЭДС и напряжений необходимо, во-первых, для правильного составления уравнений Кирхгофа при расчете электрических цепей, а во-вторых – для анализа магнитных цепей, так как направление магнитных потоков зависит от направления токов в проводниках.
Амплитуда– наибольшее значение переменного тока. Амплитуда – это мгновенное значение, которое достигается в моменты времени, для которых угол 
. Амплитуда тока обозначается прописной буквой с индексом – Im. Аналогично обозначаются амплитуды напряжений – Um и ЭДС – Em.
Периодом Т называется наименьший промежуток времени, за который мгновенное значение тока, пройдя полный цикл, достигает первоначального значения. Период измеряется в секундах [c].
Частотапеременного тока (циклическая) – величина, обратная периоду
.
Так как время Т измеряется в секундах, частота f измеряется в 
или герцах. На практике, как правило, пользуются понятием частоты, а не периода. Международная стандартная частота равна 50 Гц. Только в США и Японии применяется ток с частотой 60 Гц. В некоторых случаях применяется оборудование, работающее на нестандартных частотах. Например, в авиации с целью уменьшения веса оборудования используют частоту 400 – 800 Гц. В радиотехнике и технике связи передача информации осуществляется на частотах до нескольких тысяч мегагерц.
Фазаили фазовый угол – это угловое значение аргумента синусоидальной функции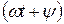 
.
Начальная фаза – значение фазы синусоидального тока в начальный момент времени t = 0: 
.
Угловая частота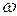 
– скорость изменения фазового угла. За время, равное периоду, фазовый угол равномерно изменяется на 2π. Поэтому угловую частоту можно определить как
;
так как 
, то угловая частота связана с циклической соотношением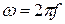 
.
Дата добавления: 2016-03-27 ; просмотров: 1506 | Нарушение авторских прав
ЛЕКЦИЯ 2
СИНУСОИДАЛЬНЫЙ ТОК. ФОРМЫ ЕГО ПРЕДСТАВЛЕНИЯ.
В практике электротехники в качестве переменного тока широкое применение нашел ток синусоидальной формы. Это обусловлено рядом преимуществ:
-генераторы синусоидального тока значительно дешевле в производстве, чем генераторы постоянного тока;
– переменный ток легко преобразуется в постоянный;
– трансформация и передача электрической энергии переменным током экономичнее чем постоянным;
-двигатели переменного тока имеют простую конструкцию, высокую надежность и невысокую стоимость.
В настоящее время переменный ток применяется в промышленном приводе и в электроосвещении, в сельском хозяйстве и на транспорте, в технике связи и в быту. Производство электрической энергии также осуществляется на переменном токе. Огромную роль в деле внедрения переменного тока сыграли русские ученые П.Н.Яблочков и М.О.Доливо-Добровольский.
Основные параметры синусоидального тока
Переменным называют ток (напряжение, ЭДС), изменяющийся во времени по величине и направлению. Синусоидальный ток может быть представлен посредством действительной функции времени – синусной и косинусной, например:
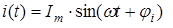(2.1)
где Im – максимальная амплитуда тока (амплитудное значение);
w – угловая частота, причем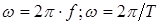 
;
f – частота колебаний [Гц];
ji – начальная фаза, определяет значение тока в момент времени t=0, т.е.
На рис. 2.1 приведен график двух колебаний с разными начальными фазами j1 и j2, причем j1 > j2. Амплитуда гармоник проходит через нуль, когда:
.
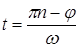Начальная фаза часто задается в градусах. Поэтому при определении мгновенного значения тока аргумент синуса ( слагаемые wt и j) нужно привести к одной единице измерения (рад. или градус).
Иногда гармоническое колебание представляется в косинусной форме. Легко видеть, что для перехода к такой форме в (2.1) достаточно изменить лишь начальную фазу, т.е.:
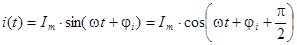
Промышленная частота переменного тока в России и всех странах Европы равна 50 Гц, в США и Японии – 60 Гц, в авиации – 400 Гц. Снижение частоты ниже 50 Гц ухудшает качество освещения. Увеличение частоты ухудшает условия передачи электроэнергии на большие расстояния.
Выражение для синусоидального напряжения аналогично (2.1), т.е.:
Аналогично (2.1) определяются и основные параметры напряжения.
Кроме уже названных параметров, в практике электротехники часто пользуются понятиями среднего и действующего значений тока и напряжения. Рассмотрим их.
Под средним значением синусоидального тока понимают его среднее значение за полпериода:
(2.3)
Видим, что среднее значение синусоидального тока составляет 2/p » 0,64 от амплитудного. Аналогично определяется среднее значение синусоидального напряжения
.
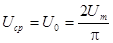Действующим называют среднее квадратичное значение синусоидального тока (напряжения) за период:
.
,
.
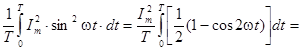
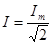Видим, что действующее значение синусоидального тока составляет 0,707 от амплитудного. Аналогично определяется действующее значение синусоидального напряжения:
.
Если говорят о значениях переменного тока или напряжения, то, как правило, подразумевают их действующее значения. Например, напряжение в однофазной сети переменного тока 220 В – действующее. При этом амплитудное значение Um @ 310 В.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8460 – 
| 7349 – 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Ток, периодически меняющийся по величине и направлению, называется переменным током. Представление о переменном токе можно получить, если медленно вращать ручку действующей модели генератора, подключенного к гальванометру. Отклонение стрелки гальванометра то вправо, то влево говорит о периодическом изменении величины и направления тока в цепи, т. е. о переменном токе.
Переменный ток, используемый в производстве и быту, изменяется по синусоидальному закону:
где i – значение переменного тока в любой момент времени, называемое мгновенным значением переменного тока. Величина Im, стоящая перед знаком синуса, называется амплитудой переменного тока.
Действующим значением переменного тока называется постоянный ток, который за время одного периода оказывает такое тепловое (механическое и др.) действие, как и данный переменный ток. Действующее значение для данного переменного тока есть величина постоянная и равная амплитудному значению, деленному на √2, т. е.
| IД = | Im |
| √2 |
Все определения и соотношения действующего значения переменного тока справедливы и для переменного напряжения.
Амперметр и вольтметр, работа которых основана на тепловом или механическом действии, при измерении переменного тока и напряжения показывают их действующие значения.
1. Мгновенное значение – величина тока соответствующая данному моменту времени
2. Амплитуда – это наибольшее положительное или отрицательное значение переменного тока. Величина ω, стоящая под знаком синуса, является угловой скоростью. Произведение угловой скорости на время (ωt) представляет собой угол, возрастающий со временем.
Графиком переменного тока является синусоида (см. рис.).
Амплитуда – максимальное мгновенное значение ( наибольшее значение, которого достигает переменный ток).
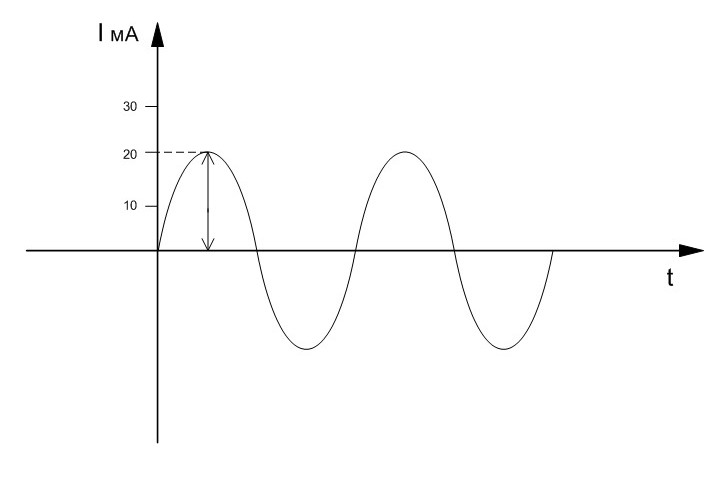
Здесь амплитуда 20 мА
3. Периодом (T) называется время, в течение которого происходит полное изменение (колебание) тока в проводнике.
Обозначается буквой Т
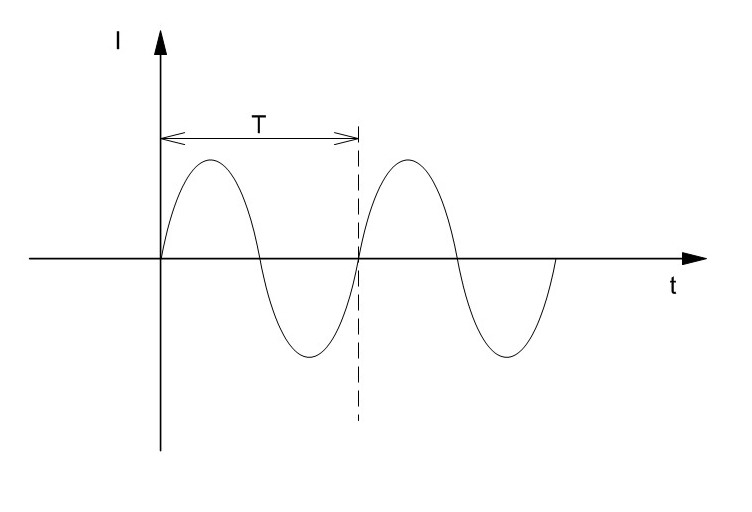
За один период совершается одно колебание переменного тока, т. е. период это время одного колебания. Одно колебание состоит из двух движений тока.
Частотой (f) называется величина, выражающаяся числом полных колебаний тока за одну секунду. Частота измеряется в герцах (Гц). При частоте в 1 Гц происходит одно полное колебание тока за одну секунду.
Стандартной частотой переменного тока в СССР является частота 50 Гц, что соответствует 50 полным колебаниям тока за одну секунду.
Частота – величина, обратная периоду. Следовательно,
f = 1/T или T = 1/f
Переменный ток, как и постоянный, оказывает тепловое, механическое, магнитное и химическое действия. В формулы расчета теплового, механического, магнитного и химического действий переменного тока подставляется действующее значение переменного тока.
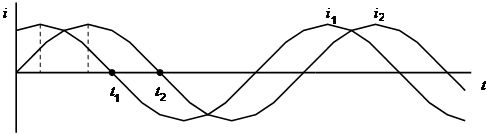
5. Фаза – это состояние переменного тока за определенный период времени
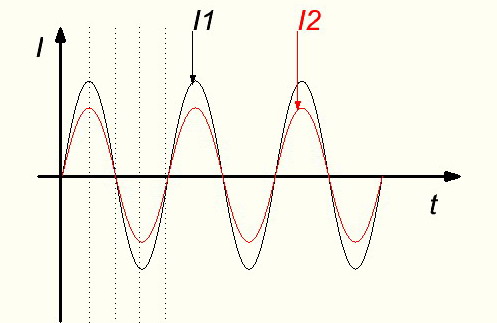
Переменные величины могут совпадать по фазе. Это значит что они одновременно достигают нулевых значений и одновременно достигают максимальных значений одинаковых направлений.
Здесь токи I1 и I2 совпадают по фазе
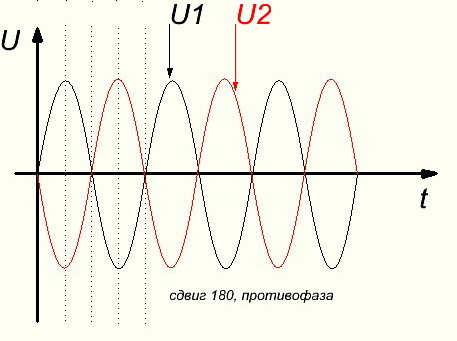
Здесь напряжения U1 и U2 находятся в противофазе.
Это значит что они одновременно достигают нулевых и максимальных значений противоположных направлений.
Если переменные величины не совпадают по фазе, то говорят что они сдвинуты по фазе. Сдвиг по фазе выражается в градусах или в долях периода. Весь период 360 0 , так как период получается за один полный оборот проводника по окружности в магнитном поле.
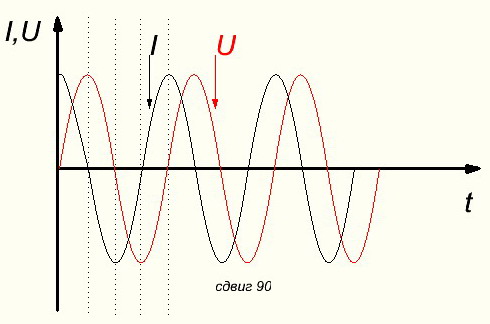
Здесь напряжение отстает от тока на 90 0 , т. е . ток и напряжение сдвинуты по фазе на 90 0 .
Действительно в начале ток уже достиг максимума, а напряжение находится на нуле. Напряжение достигнет максимума через 90 0 .
Сдвиг по фазе обозначается греческой буквой φ например φ=90 0 .
Допустим, что до отключения в цепи рис. 4.5, а был установившийся ток I = U/r и энергия магнитного поля катушки составляла
Казалось бы, после размыкания выключателя ток должен мгновенно прекратиться. Однако на основании первого закона коммутации при t = 0+ ток сохраняет свое прежнее значение.
| Рис. 4.5. Отключение цепи r, L(а) от сети постоянного тока; без разрядного резистора (а), с разрядным резистором (б); зависимости i(t) (в) и uL(t)(г) при отключении цепи r, L с разрядным резистором |
Возникает как будто несоответствие: цепь разомкнута, ток есть. В действительности при размыкании выключатели происходит следующее. Ток уменьшается, и в катушке индуктируется значительная ЭДС. При этом напряжение между контактами выключателя, равное сумме напряжения сети и ЭДС самоиндукции, пробивает воздушный промежуток между контактами — возникает электрическая дуга и электрическая цепь оказывается замкнутой. По мере увеличения расстояния между контактами сопротивление дуги возрастает, ток и ЭДС уменьшаются и цепь оказывается разомкнутой. За время переходного процесса энергия магнитного поля катушки выделяется в виде теплоты в электрической дуге и сопротивлении катушки.
Переходный процесс в этом случае получается довольно сложным вследствие того, что сопротивление дуги нелинейное и изменяется во времени.
Отключение цепи с индуктивностью вызывает обгорание контактов размыкающего устройства и появление значительных ЭДС и напряжения на выводах катушки, превышающих в несколько раз напряжение сети (это может привести к пробою изоляции катушки).
Во избежание этого в силовых цепях, обладающих значительной индуктивностью (обмотки возбуждения генераторов и двигателей постоянного тока, синхронных двигателей, магнитных плит и т. п.), параллельно обмоткам включают разрядные резисторы (рис. 4.5, б).
В этом случае после отключения выключателя катушка индуктивности (r, L) оказывается замкнутой на разрядное сопротивление r р . Ток в цепи будет убывать значительно медленнее. По этой причине значение возникающей ЭДС будет существенно меньше, чем без разрядного резистора, и возникшая слабая дуга исчезает почти мгновенно. В последующих рассуждениях и выводах предполагается, что дуга между контактами не возникает и цепь размыкается мгновенно.
Уравнение цепи, составленное по второму закону Кирхгофа, имеет вид