В какой колебательной системе может наблюдаться резонанс

Если колебания совершаются в системе за счет первоначально сообщенной энергии, то они называются свободными. Примером таких систем являются модели колеблющихся тел:математическиймаятник ипружинный.

Вынужденные колебания– колебания, происходящие под действием меняющейся во времени внешней силы, которая совершает работу. За счет этого энергия колебательной системы увеличивается. Такой процесс можно описывать как процесс притока энергии в систему извне в ходе самих колебаний. Примером систем, в которых происходят вынужденные колебания, являются качели, раскачиваемые человеком, груз, висящий на пружине, точку подвеса которой периодически поднимают и опускают.

Если внешняя сила, действующая на систему, изменяется с течением времени по закону косинуса или синуса, то возникающие в системе вынужденные колебания будут гармоническими. При этом частота вынужденных колебаний будет совпадать с частотой изменения внешней силы.

Если при вынужденных колебаниях энергия, поступающая непрерывно или периодически от внешнего источника, восполняет потери, возникающие за счет работы силы трения, то колебания оказываются незатухающими.

Амплитуда вынужденных колебаний определяется амплитудой колебаний внешней силы, а также соотношением между частотой изменения этой силы и собственной частотой колебательной системы.

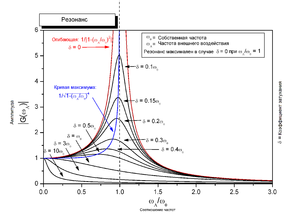
При вынужденных колебаниях может наблюдаться явление резкого возрастания амплитуды Aвынужденных колебаний системы –резонанс. Это явление возникает тогда, когда частота вынуждающей силы приближается к собственной частоте колебаний этой системы. При этом энергия, поступающая в колебательную систему, также равна потерям энергии за счет работы силы трения, однако баланс энергий наступает при другой амплитуде колебаний.

Резонанс может возникать и тогда, когда частота колебаний вынуждающей силы кратна собственной частоте колебаний системы.

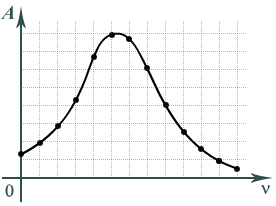
Зависимость амплитуды колебаний системы от частоты вынуждающей силы (рис. 7) называется резонансной кривой.

В технике используются устройства, в которых незатухающие колебания поддерживаются за счет энергии источника, автоматически включаемого и выключаемого самой колебательной системой. Момент, когда требуется подать энергию в колеблющуюся систему, отслеживает система обратной связи, которая открывает и закрывает клапан поступления энергии. Такие системы с регулированием поступления энергии за счет обратной связи называются автоколебательными, а сами колебания в таких системах – автоколебаниями.Примером такой системы могут служить маятниковые часы, где источником энергии является гиря на цепочке, роль обратной связи и «клапана» выполняет анкерный механизм, а автоколебания совершает маятник, который имеет собственную частоту колебаний, равную 1с

15. Механические волны. Виды волн. Длина волны.

В среде между ее частицами существуют силы взаимодействия. Если за счет внешнего источника энергии (внешней силы) вызвать колебания одних частиц среды, то возникают вынужденные колебания соседних частиц, которые, в свою очередь, вызывают колебания следующих частиц среды. Процесс распространения колебанийчастиц среды или другого типа возмущения среды называютмеханической волной.

Волны, в которых колебания частиц происходят вдоль направления распространения волны, называются продольными.

Волны, в которых колебания частиц происходят перпендикулярно направлению распространения волны, называются поперечными.

В продольной волне возмущения представляют собой сжатие (или разрежение) среды, а в поперечной – смещение (сдвиг) одних слоев среды относительно других. Пример продольных волн – распространение звука (зон сжатия) в газах, жидкостях и твердых телах, пример поперечных волн – распространение звука в твердом теле, волны на поверхности воды, на веревке или на пружине.

Деформация сжатия всегда сопровождается возникновением силы упругости, в то время как деформация сдвига приводит к появлению сил упругости только в твердых телах; сдвиг слоев в газах и жидкостях возникновением сил упругости не сопровождается. Поэтому продольные волны могут распространяться во всех средах: жидких, твердых, газообразных, а поперечные – только в твердых.

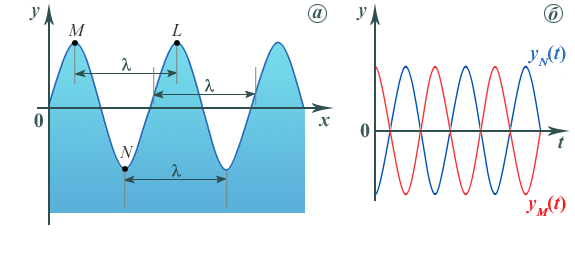
График зависимости смещения каждой частицы среды от времени представляет собой синусоиду, сдвинутую относительно синусоиды для частицы в другой точке в соответствии со сдвигом фаз (рис. 2,б) Минимальное расстояние между точками волны, колеблющимися в фазе, т.е. с разностью фаз, равной 2, называютдлиной волны.

Геометрическое место положений точек волны в момент времени tтакже представляет собой синусоиду (см. рис. 2,а) вида

Аналогичные соотношения можно записать и для продольной волны, только в ней y(t,x) будет смещением частиц среды относительно положения равновесия вдоль осиx, по которой распространяется волна.

Резонанс в линейных системах с одной степенью свободы

Пример простейшего случая резонанса представляют вынужденные колебания, возбуждаемые сторонним источником – гармонической э.д.с.

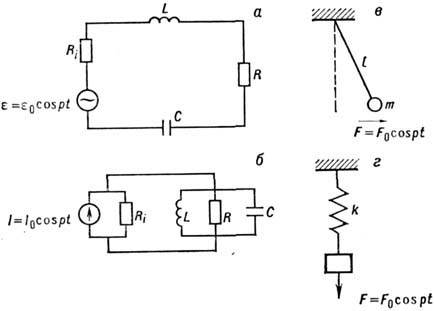
Рис. 1. Колебательные системы с одной степенью свободы: последовательный (а) и параллельный (б) колебательные контуры, математический маятник (в) и упругий осциллятор (г),

Амплитуда x и фаза φ вынужденных колебаний заряда [q(t) = xcos(pt + φ)] определяются амплитудой и частотой внешней силы:

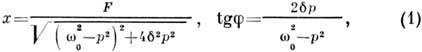
Зависимость амплитуды х стационарных вынужденных колебаний от частоты p вынуждающей силы при постоянной её амплитуде называется резонансной кривой (рис. 2). В линейном колебательном контуре резонансные кривые, соответствующие различным F, подобны, а фазово-частотная характеристика f(p) не зависит от амплитуды силы.

Вложение энергии в колебательный контур пропорциональна первой степени, а диссипация энергии пропорциональна квадрату амплитуды колебаний. Это обеспечивает ограничение амплитуд стационарных вынужденных колебаний при резонансе. Приближение частоты p к собственной частоте w₀ сопровождается ростом амплитуды вынужденных колебаний, тем более резким, чем меньше коэффицикнт затухания d. При резонансе ток, протекающий через контур, I = 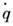= pxcos(pt + φ – p/2), находится в фазе с э.д.с. стороннего источника (f = p/2). Уменьшение амплитуды вынужденных колебаний при неточной настройке обусловлено нарушением синфазности тока и напряжения в цепи.

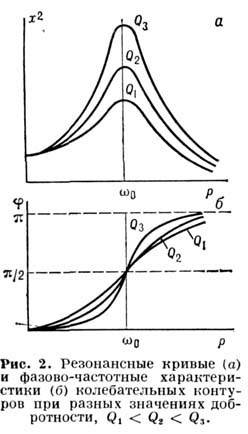
Важной характеристикой резонансных свойств колебательной системы (осциллятора) является добротность Q, которая, по определению, равна умноженному на 2p отношению энергии, запасённой в системе, к энергии, рассеиваемой за период колебаний. При воздействии на резонансной частоте амплитуда вынужденных колебаний x в Q-раз больше, чем в квазистатическом случае, при 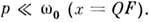. Число периодов колебаний, в течение которых происходит установление стационарной амплитуды, также пропорционально Q. Наконец, добротность определяет частотную избирательность резонансных систем. Ширина полосы резонанс Dw, в пределах которой амплитуда вынужденных колебаний спадает в 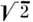-раз от х, обратно пропорциональна добротности: Dw = w₀/Q = 2d.

При резонансе в электрических цепях реактивная часть комплексного импеданса обращается в нуль. При этом в последовательной цепи падения напряжения на катушке индуктивности и на конденсаторе имеют амплитуду QE₀. Однако они складываются в противофазе и взаимно компенсируют друг друга. В параллельной цепи (рис. 1, б)при резонанс происходит взаимная компенсация токов в ёмкостной и индуктивной ветвях. В отличие от последовательного резонанса, при котором внешнее силовое воздействие осуществляется источником напряжения, в параллельном контуре резонансные явления реализуются только в том случае, когда внешнее воздействие задаётся источником тока. Соответственно резонанс в последовательном контуре называют резонансом напряжений, а в параллельном контуре – резонансом токов. Если в параллельный контур вместо генератора тока включить генератор напряжения, то на резонансной частоте будут выполняться условия не максимума, а минимума тока, поскольку вследствие компенсации токов в ветвях, содержащих реактивные элементы, проводимость цепи оказывается минимальной (явление антирезонанса).

Подобными чертами обладает явление резонанса в механических и других колебательных системах. В линейных системах, согласно принципу суперпозиции, реакцию системы на периодическое несинусоидальное воздействие можно найти как сумму откликов на каждую из гармонических компонент воздействия. Если период несинусоидальной силы равен Т, то резонансное возрастание колебаний может происходить не только при условии w₀ ! 2p/Т, но в зависимости от формы E(t)и при условиях w₀ ! 2pn/T, где n = 1, 2. (резонанс на гармониках).

Резонансные кривые определяют, наблюдая изменение амплитуды вынужденных колебаний либо при медленной перестройке частоты p вынуждающей силы, либо при медленном изменении собственной частоты w₀. При высокой добротности осциллятора (Q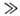1) оба способа дают практически одинаковые результаты. Частотные характеристики, полученные при конечной скорости изменения частоты, отличаются от статических резонансных кривых, соответствующих бесконечно медленной перестройке: на динамических частотных характеристиках наблюдается смещение максимума в направлении перестройки частоты, пропорц. m, где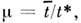 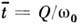– время релаксации колебаний в контуре, t* – время, в течение котоpогo частота p находится в пределах полосы резонанса Dw. При быстрой перестройке частоты, по мере роста m, происходит уменьшение высоты и расширение резонансных кривых, причём их форма становится более асимметричной (рис. 3).

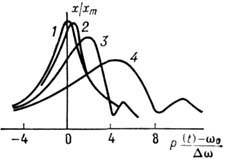
Рис. 3. Статические и динамические амплитудно-частотные характеристики резонанса
при различных скоростях нарастания частоты: p(t)= w₀ + t/m, m = 0(1), 0,0625 (г), 0,25(3), 0,695 (4).

Резонанс в линейных колебательных системах с несколькими степенями свободы

Колебательные системы с нескими степенями свободы представляют собой совокупность взаимодействующих осцилляторов. Примером может служить пара колебательных контуров, связанных за счёт взаимной индукции (рис. 4). Вынужденные колебания в такой системе описываются уравнениями

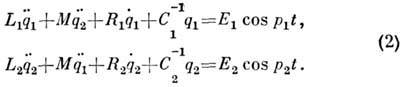
Индуктивная связь приводит к тому, что колебания в отдельных контурах не могут происходить независимо друг от друга. Однако для любой колебательной системы с нескими степенями свободы можно найти нормальные координаты, которые являются линейными комбинациями независимых переменных. Для нормальных координат система уравнений, подобная (2), преобразуется в цепочку уравнений для вынужденных колебаний такого же вида, как для одиночных колебательных контуров, с тем отличием, что воздействие на каждую из нормальных координат оказывают силы, приложенные, вообще говоря, в разных частях совокупной колебательной системы. При рассмотрении законов движения в нормальных координатах справедливы все закономерности резонанса в системах с одной степенью свободы.

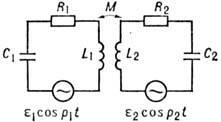
Рис. 4. Колебательная система с двумя степенями свободы – пара контуров со связью за счёт взаимоиндукции.

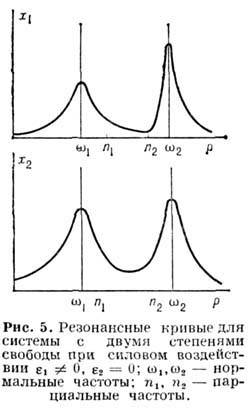
Резонансное нарастание колебаний происходит во всех частях колебательной системы на одних и тех же частотах (рис. 5), равных частотам собственных колебаний системы. Нормальные частоты не совпадают с парциальными, т. е. с собств. частотами осцилляторов, входящих в совокупную систему. Если частота сторонней силы равна одной из парциальных частот, то в совокупной системе резонанс не наступает. Напротив, в этом случае амплитуды вынужденных колебаний достигают минимума, аналогично случаю антирезонанса в системе с одной степенью свободы. Возможность подавления колебаний, частота к-рых равна одной из парциальных, используется в электрич. фильтрах и успокоителях механич. колебаний.

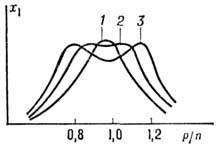
Рис. 6. Резонансные кривые двухконтурной колебательной
системы при gQ = 1(1), 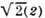и 2(3); g = M/L, L₁ = L₂.

В системе, состоящей из слабо связанных осцилляторов с одинаковыми парциальными частотами, резонансные максимумы, отвечающие близким нормальным частотам, могут сливаться, так что частотная характеристика имеет один максимум (рис. 6). Увеличение связи между осцилляторами приводит к росту интервала между нормальными частотами системы. Изменение формы резонансных кривых при увеличении коэффициента связи иллюстрирует рис. 6. Система осцилляторов при связи, близкой к критической, имеет частотную характеристику, уплощённую вблизи резонанса, причём крутизна её склонов выше, чем у одиночного осциллятора с таким же уровнем потерь. Это свойство обычно используется для создания полосовых электрических фильтров.

Резонанс в распределённых колебательных системах

В распределённых системах (см. Система с распределёнными параметрами)амплитуда и фаза колебаний зависят от пространственных координат. Линейные распределённые колебательные системы характеризуются набором нормальных частот и собственных функций, которые описывают пространственное распределение амплитуд собственных колебаний. Резонансные свойства (добротность) распределённых систем определяются не только собств. затуханием, но и связью с окружающей средой, в которую происходит излучение части энергии колебаний (электрич., упругих и других). В распределённых системах, обладающих высокой добротностью (Q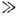1), вынужденные колебания представляют собой стоячие волны, пространственное распределение амплитуд которых является суперпозицией собственных функций (мод), а фаза колебаний одинакова во всех точках. Действие сторонних сил с частотами, близкими к собственным, ведёт к резонансному нарастанию амплитуды вынужденных колебаний во всех точках объёма распределённой резонансной системы (резонатора).

В распределённых системах сохраняют силу все общие свойства резонанса. Особенностью резонанса в распределённых системах (равно как и в системах с неск. степенями свободы) является зависимость амплитуд вынужденных колебаний не только от частоты, но и от пространственного распределения вынуждающей силы. Резонанс наступает, если пространственное распределение внеш. силы повторяет форму собств. функции, а частота равна соответствующей нормальной частоте. При неблагоприятном пространственном распределении сторонней силы вынужденные колебания не возбуждаются. Это происходит, в частности, тогда, когда сосредоточенная сила прикладывается в точках, для которых амплитуда соответствующего нормального колебания обращается в нуль. Так, прикладывая сосредоточенную силу в точке, являющейся узловой для перемещений струны, невозможно возбудить её колебания, поскольку работа силы будет равна нулю. Если распределение сил таково, что работа, совершаемая ими в различных частях системы, имеет противоположные знаки и в целом не приводит к изменению энергии, вынужденные колебания также не возбуждаются.

Резонанс в нелинейных колебательных системах

В упругих системах нелинейным элементом является пружина, для к-рой связь между деформацией и упругой силой нелинейна, т. е. нарушается закон Гука. В электрич. системах примером нелинейного диссипативного элемента является диод, вольт-амперная характеристика к-рого не подчиняется закону Ома. Нелинейными реактивными (энергоёмкими) элементами являются конденсаторы с сегнетоэлектриком или катушки индуктивности с ферритовыми сердечниками. Параметры этих элементов – ёмкость, индуктивность, сопротивление, а также собств. частоту и коэф. затухания в нелинейных системах можно считать функциями тока или напряжения. При этом в нелинейных системах не выполняется суперпозиции принцип.

В нелинейных системах гармонич. сила возбуждает негармонич. колебания, в спектре к-рых имеются кратные частоты, поэтому резонанс на гармониках происходит p при синусоидальной внеш. силе. В колебат. системах, обладающих достаточно высокой добротностью и частотной избирательностью, наиб. амплитуду имеет та спектральная компонента, частота к-рой близка к частоте резонанс Рассматривая лишь колебания с частотой, близкой к резонансной, можно и в этом случае получить семейство резонансных кривых. Для системы с нелинейными реактивными (энергоёмкими) элементами при r ! w₀ эти кривые изображены на рис. 7. Форма резонансной кривой зависит от амплитуды вынуждающей силы и по мере её увеличения становится всё более асимметричной. Поскольку частота собств. колебаний нелинейного осциллятора зависит от их амплитуды, то и максимумы на резонансных кривых сдвигаются в сторону более высоких или более низких частот. Начиная с нек-рого значения амплитуды силы, резонансные кривые приобретают неоднозначную клювообразную форму. В определённом интервале частот стационарная амплитуда вынужденных колебаний оказывается зависящей от предыстории установления колебаний (явление колебат. гистерезиса). При этом части резонансных кривых, соответствующих неустойчивым состояниям, образуют на плоскости (х, р)область физически нереализуемых режимов (на рис. 7 заштрихована).

Рис. 7. Семейство амплитудно-частотных кривых в случае нелинейного резонанса при различных амплитудах сторонней силы (F₁ к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Резона́нс (фр. resonance , от лат. resono «откликаюсь») — частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы [1] . Для линейных колебательных систем значения частот резонанса совпадает с частотами собственных колебаний, а их число соответствует числу степеней свободы [1] .

Под действием резонанса, колебательная система оказывается особенно отзывчивой на действие внешней силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

Явление резонанса впервые было описано Галилео Галилеем в 1602 г. в работах, посвященных исследованию маятников и музыкальных струн. [2] [3]

Содержание

Механика [ править | править код ]

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если подталкивать качели в определённые моменты времени в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния можно найти по формуле:

f = 1 2 π g L <displaystyle f=<1 over 2pi ><sqrt >> ,

где g — это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна и включает эллиптический интеграл.) Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут приводить как к разрушению, так и к усилению устойчивости механических систем.

В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую и наоборот. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Струна [ править | править код ]

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины, массы и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, её частота зависит от скорости v, с которой волна распространяется по струне:

f = v 2 L <displaystyle f=>

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

v = T ρ <displaystyle v=<sqrt >>

Таким образом, частота главного резонанса может зависить от свойств струны и выражается следующим отношением:

f = T ρ 2 L = T m / L 2 L = T 4 m L <displaystyle f=<<sqrt > over 2L>=<<sqrt > over 2L>=<sqrt >> ,

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f [4] , и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Электроника [ править | править код ]

В электрических цепях резонансом называется такой режим пассивной цепи, содержащий катушки индуктивности и конденсаторы, при котором ее входное реактивное сопротивление или ее входная реактивная проводимость равны нулю. При резонансе ток на входе цепи, если он отличен от нуля, совпадает по фазе с напряжением.

В электрических цепях резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно (тогда возникает резонанс напряжений), так и параллельно (резонанс токов). При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

ω L = 1 ω C ⇒ ω = 1 L C <displaystyle omega L=<frac <1><omega C>>Rightarrow omega =<frac <1><sqrt >>> ,

где ω = 2 π f <displaystyle omega =2pi f> ; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.

В электронных устройствах также применяются различные электромеханические резонансные системы.

СВЧ [ править | править код ]

В СВЧ электронике широко используются объёмные резонаторы, чаще всего цилиндрической или тороидальной геометрии с размерами порядка длины волны, в которых возможны добротные колебания электромагнитного поля на отдельных частотах, определяемых граничными условиями. Наивысшей добротностью обладают сверхпроводящие резонаторы, стенки которых изготовлены из сверхпроводника и диэлектрические резонаторы с модами шепчущей галереи.

Оптика [ править | править код ]

В оптическом диапазоне самым распространенным типом резонатора является резонатор Фабри-Перо, образованный парой зеркал, между которыми в резонансе устанавливается стоячая волна. Применяются также кольцевые резонаторы с бегущей волной и оптические микрорезонаторы с модами шепчущей галереи.

Акустика [ править | править код ]

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, корпус у барабанов.

Для акустических систем и громкоговорителей резонанс отдельных элементов (корпуса, диффузора) является нежелательным явлением, так как ухудшает равномерность амплитудно-частотной характеристики устройства и верность звуковоспроизведения. Исключением являются акустические системы с фазоинвертором, в которых намеренно создаётся резонанс для улучшения воспроизведения низких частот.

Астрофизика [ править | править код ]

Орбитальный резонанс в небесной механике — это ситуация, при которой два (или более) небесных тела имеют периоды обращения, которые относятся как небольшие натуральные числа. В результате эти небесные тела оказывают регулярное гравитационное влияние друг на друга, которое может стабилизировать их орбиты.