Содержание
Вектор магнитной индукции (В) – это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М.
Бесконечно длинный ток величины I создает на расстоянии r от себя магнитное поле:
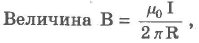 где Мо – магнитная постоянная, R – расстояние, I – сила тока в проводнике.
где Мо – магнитная постоянная, R – расстояние, I – сила тока в проводнике.
Магнитная индукция – это векторная физическая величина, являющаяся силовой характеристикой в данной точке магнитного поля.
Единица магнитной индукции – тесла (Тл).
Магнитная индукция 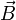 — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой
— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой 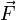 магнитное поле действует на заряд
магнитное поле действует на заряд 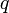 , движущийся со скоростью
, движущийся со скоростью 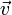 .
.
В вакууме B = μ0H.
Более конкретно, 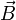 — это такой вектор, что сила Лоренца
— это такой вектор, что сила Лоренца 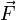 , действующая со стороны магнитного поля на заряд
, действующая со стороны магнитного поля на заряд 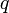 , движущийся со скоростью
, движущийся со скоростью 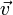 , равна
, равна
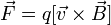
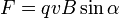
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора 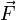 перпендикулярно им обоим и направлено по правилу буравчика).
перпендикулярно им обоим и направлено по правилу буравчика).
Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции.
Опытным путем было установлено, что для одной и той же точки магнитного поля максимальный вращающий момент М (момент сил) пропорционален произведению силы тока I в контуре на его площадь S. Величину IS называют магнитным моментом контура Pm.
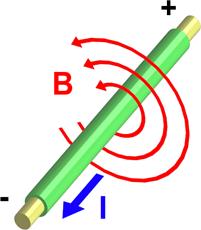 Рисунок– Электрический ток (I), проходя по проводнику, создаёт магнитное поле (B) вокруг проводника. Рисунок– Электрический ток (I), проходя по проводнику, создаёт магнитное поле (B) вокруг проводника. |
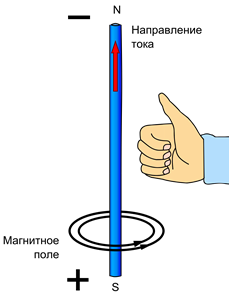 Рисунок – Правило буравчика Рисунок – Правило буравчика |
Правило буравчика (винта): Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.
На практике удобно пользоваться следующим правилом: Если обхватить соленоид (катушку) правой рукой так, что бы четыре пальца были направлены по току, то отогнутый большой палец покажет направление магнитного поля внутри соленоида.
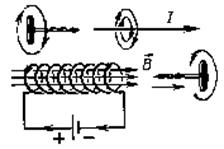
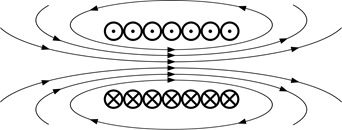
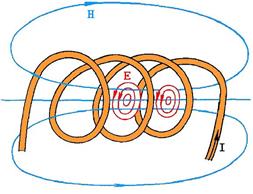
Рисунок 3.2 – А) Образование магнитного потока в соленоиде
Б) Схема полей в соленоиде при протекании по обмотке переменного тока
Единица измерения В в СИ – тесла (Тл). Единица названа в честь сербского электротехника Н. Тесла. 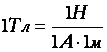
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10093 –  | 7529 –
| 7529 –  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Здесь изложены основные формулы теории магнетизма. Информация для школьников, студентов и всех кого интересует этот вопрос
Правило правой руки или буравчика:
Направление силовых линий магнитного поля и направление создающего его тока связаны между собой известным правилом правой руки или буравчика, которые ввел еще Д.Максвелл и иллюстрируется следующими рисунками:
 |
 |

Мало кто знает, что буравчик – это инструмент для бурения-сверления отверстий в дереве. Поэтому более понятно можно это правило назвать правилом винта, шурупа или штопора. Однако хвататься за провод как на рисунке иногда опасно для жизни!
Магнитная индукция B :
 Магнитная индукция – является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряженности электрического поля E . Вектор магнитной индукции всегда направлен по касательной к магнитной линии и показывает ее направление и силу. За единицу магнитной индукции в B = 1Тл
Магнитная индукция – является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряженности электрического поля E . Вектор магнитной индукции всегда направлен по касательной к магнитной линии и показывает ее направление и силу. За единицу магнитной индукции в B = 1Тл  принимается магнитная индукция однородного поля, в котором на участок проводника длиной в l = 1 м, при силе тока в нем в I = 1 А, действует со стороны поля максимальная сила Ампера – F = 1 H. Направление силы Ампера определяется по правилу левой руки . В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл).
принимается магнитная индукция однородного поля, в котором на участок проводника длиной в l = 1 м, при силе тока в нем в I = 1 А, действует со стороны поля максимальная сила Ампера – F = 1 H. Направление силы Ампера определяется по правилу левой руки . В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл).
Напряженность магнитного поля H :
Еще одной характеристикой магнитного поля является напряженность, которая является аналогом вектора электрического смещения D в электростатике. Определяется по формуле:

Напряженность магнитного поля – величина векторная, является количественной характеристикой магнитного поля и не зависит от магнитных свойств среды. В системе СГС напряженность магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м).
Магнитный поток Ф:
Магнитный поток Ф – скалярная физическая величина, характеризующая число линий магнитной индукции, пронизывающих замкнутый контур.  Рассмотрим частный случай. В однородном магнитном поле , модуль вектора индукции которого равен ∣ В ∣, помещен плоский замкнутый контур площадью S. Нормаль n к плоскости контура составляет угол α с направлением вектора магнитной индукции B . Магнитным потоком через поверхность называется величина Ф, определяемая соотношением:
Рассмотрим частный случай. В однородном магнитном поле , модуль вектора индукции которого равен ∣ В ∣, помещен плоский замкнутый контур площадью S. Нормаль n к плоскости контура составляет угол α с направлением вектора магнитной индукции B . Магнитным потоком через поверхность называется величина Ф, определяемая соотношением:

В общем случае магнитный поток определяется как интеграл вектора магнитной индукции B через конечную поверхность S.

Стоит отметить, что магнитный поток через любую замкнутую поверхность равен нулю (теорема Гаусса для магнитных полей). Это означает, что силовые линии магнитного поля нигде не обрываются т.е. магнитное поле имеет вихревую природу, а также что невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле. В СИ единицей магнитного потока является Вебер (Вб), в системе СГС — максвелл (Мкс); 1 Вб = 10 8 Мкс.
 Индуктивность — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур.
Индуктивность — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур.

Иначе, индуктивность – коэффициент пропорциональности в формуле самоиндукции .

В системе единиц СИ индуктивность измеряется в генри (Гн). Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать ЭДС самоиндукции в один вольт.
Термин «индуктивность» был предложен Оливером Хевисайдом – английским ученым-самоучкой в 1886 году. Говоря просто, индуктивность это свойство проводника с током накапливать энергию в магнитном поле, эквивалентна емкости для электрического поля. Она не зависит от величины тока, а только от формы и размеров проводника с током. Для увеличения индуктивности проводник наматывают в катушки, расчету которых и посвящена программа Coil32
Один из параметров магнитного поля – его силовая характеристика. Она обозначает, с какой силой поле влияет на движущиеся в нём заряженные частицы. Это значение из разряда векторных величин, носит название магнитная индукция B→.

Физический смысл магнитной индукции (МИ)
Возможность действовать на предмет магнитным полем (МП) определяет сущность настоящей индукции. Она появляется в момент перемещения в катушке индуктивности магнита постоянной природы. Результатом такого движения является появление тока, с одновременным увеличением магнитного потока. Поскольку обмотка у катушки металлическая, а структура металла – кристаллическая решётка, то можно объяснить физические свойства этого явления.
Электроны, находящиеся в этой решётке, при отсутствии магнитного воздействия находятся в покое. Движения никакого нет. Оно начинается в тот момент, когда электроны попадают под воздействие переменного МП (поле изменяется при перемещении постоянного магнита).
Значение возникающего в катушке тока зависит от диаметра жилы и количества витков, физических характеристик магнита и скорости его движения.
Единица размерности в системе Си рассматриваемой характеристики – тесла. Она обозначается буквами Тл.
Важно! Электроны в решётке, после попадания катушки в МП, разворачиваются под некоторым углом и выстраиваются вдоль силовых линий МП. Количество ориентированных частиц и однородность их размещения зависимы от величины поля.
Вектор – это вектор индукции магнитного поля (градиентный параметр МП).

Направление вектора МИ
Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.
Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.
Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали.
В некоторых случаях, чтобы найти направление, применяют правило правой руки.

Наглядное отображение линий МИ
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.
С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.

Модуль вектора магнитной индукции
Чтобы определить величину вектора МИ, нужно узнать его модуль. Как определяется модуль вектора магнитной индукции (градиент)? Это можно понять на примере небольшой модели. Если поместить в поле подковообразного магнита горизонтально подвешенный проводник, то МП магнита будет действовать только на участок, расположенный в междуполюсном промежутке. Сила F→, действующая на этот участок, будет направлена под прямым углом к линиям индукции и самому проводнику. Она достигает своего максимума, когда орт МИ располагается перпендикулярно проводнику.
Значение модуля B→ будет равно отношению максимального значения этой силы F→ к произведению длины отрезка ∆L на силу движения зарядов (I), а именно:

Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.
Закон Био-Савара-Лапласа
Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.
Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:
dB = µ0 *I*dl*sin α /4*π*r2,
где:
- dB – магнитная индукция, Тл;
- µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
- I – сила тока, А;
- dl – отрезок проводника, м;
- r – расстояние до точки нахождения магнитной индукции, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.

Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого перемещения электронов;
- поля кругового движения заряженных частиц.
Формула для МП первого типа имеет вид:
Для кругового движения она выглядит так:
В этих формулах µ – это магнитная проницаемость среды (относительная).
Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:

Теорема о циркуляции
Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.
Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.
Другое название теоремы – закон Ампера, описывающий циркуляцию МП.
Математически теорема записывается следующим образом.

где:
- B→– вектор магнитной индукции;
- j→ – плотность движения электронов.
Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.
Магнитный поток
Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):
Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.
Формула для расчёта имеет вид:
где:
- В – скалярная величина градиента магнитной индукции;
- S – площадь пересекаемой поверхности;
- α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).
Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900).

Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.
