Параметры резистивных элементов, их главное свойство. Линейные и нелинейные резистивные элементы. Определение соотношения статического и дифференциального сопротивлений. Основные виды индуктивных и емкостных элементов. Примеры ВАХ нелинейных элементов.
| Рубрика | Физика и энергетика |
| Вид | презентация |
| Язык | русский |
| Дата добавления | 21.09.2016 |
| Размер файла | 144,0 K |

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Подобные документы
Нелинейные элементы и устройства электрических цепей переменного тока, основанные на этих элементах. Их классификация и краткая характеристика. Практические примеры использования нелинейных элементов на примере диодов. Диодные вентили и ограничители.
курсовая работа [1,5 M], добавлен 05.01.2017
Расчет нелинейных резистивных цепей. Преобразование электрической энергии в тепло. Безынерционные элементы как источники высших гармоник. Статическое и дифференциальное сопротивление. Закон Ома, Джоуля-Ленца. Метод эквивалентного генератора в цепях.
презентация [1,3 M], добавлен 28.10.2013
Нелинейные резистивные (безинерционные) двухполюсные и четырехполюсные элементы. Анализ нелинейных цепей с двухполюсными элементами. Сущность графоаналитических методов анализа нелинейных цепей. Анализ цепей с четырехполюсными нелинейными элементами.
реферат [155,2 K], добавлен 11.03.2009
Что такое нелинейные цепи и нелинейный элемент. Классификация нелинейных элементов, параметры и некоторые схемы замещения. Методы расчёта нелинейных цепей постоянного тока. Графический способ расчета цепей с применением кусочно-линейной аппроксимации.
реферат [686,7 K], добавлен 28.11.2010
Экспериментальное определение и построение вольтамперных характеристик нелинейных резистивных элементов. Проверка достоверности графического метода расчёта нелинейных электрических цепей. Основные теоретические положения, порядок выполнения работы.
лабораторная работа [297,6 K], добавлен 22.12.2009
Анализ соотношения между синусоидальными напряжениями и токами при последовательном и параллельном соединении резистивных, индуктивных и емкостных элементов цепи. Оценка параметров последовательной и параллельной схем замещения реальных элементов цепи.
лабораторная работа [137,0 K], добавлен 24.11.2010
Понятие и примеры простых резистивных цепей. Методы расчета простых резистивных цепей. Расчет резистивных электрических цепей методом токов ветвей. Метод узловых напряжений. Описание колебания в резистивных цепях линейными алгебраическими уравнениями.
реферат [128,0 K], добавлен 12.03.2009
Электрическая цепь как совокупность элементов и устройств, предназначенных для прохождения тока. Напряжения и токи в них. Линейные электрические цепи и принцип наложения. Понятия двухполюсника и четырехполюсника. Элементы электрических цепей и их свойства
реферат [55,8 K], добавлен 10.03.2009
Понятие и функциональные особенности нелинейных индуктивных элементов, правила их обозначения. Характеристики: статическая и дифференциальная индуктивность, веберамперная характеристика и энергия магнитного поля. Пути использования законов Кирхгофа.
презентация [517,6 K], добавлен 28.10.2013
Электромагнитные процессы, протекающие в электротехнических устройствах. Резистивный элемент, катушка индуктивности, конденсатор. Схемы замещения источников электрической энергии. Пассивные элементы цепи, их основные характеристики и параметры.
реферат [105,0 K], добавлен 14.02.2014

Работы в архивах красиво оформлены согласно требованиям ВУЗов и содержат рисунки, диаграммы, формулы и т.д.
PPT, PPTX и PDF-файлы представлены только в архивах.
Рекомендуем скачать работу.
| Название: Нелинейные элементы Раздел: Рефераты по коммуникации и связи Тип: реферат Добавлен 05:04:41 26 августа 2009 Похожие работы Просмотров: 1366 Комментариев: 13 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать |
Рис. 1
Рис.2
По однозначности: однозначные – в которых каждому значению вхо-дной величины соответствует одно значение выходной величины (рис. 3a); многозначные – в которых каждому значению входной величины х соответствует несколько значений выходной величины z (рис.3б, в, г).
По симметрии: четно-симметричные – симметричные относительно оси ординат, т. е. z(х) = z (- х) (рис. 4а); нечетно-симметричные – сим-метричные относительно начала координат, при этом z (х) = – z ( – х ) (рис. 4б); не симметричные (рис. 4в).
2. Нелинейные цепи
Нелинейными называются цепи, в состав которых входит хотя бы один нелинейный элемент. Нелинейные элементы описываются нелинейными характеристиками, которые не имеют строгого аналитического выражения, определяются экспериментально и задаются таблично или графиками.
Нелинейные элементы можно разделить на двух – и многополюсные. Последние содержат три (различные полупроводниковые и электронные триоды) и более (магнитные усилители, многообмоточные трансформаторы, тетроды, пентоды и др.) полюсов, с помощью которых они подсоединяются к электрической цепи. Характерной особенностью многополюсных элементов является то, что в общем случае их свойства определяются семейством характеристик, представляющих зависимости выходных характеристик от входных переменных и наоборот: входные характеристики строят для ряда фиксированных значений одного из выходных параметров, выходные – для ряда фиксированных значений одного из входных.
По другому признаку классификации нелинейные элементы можно разделить на инерционные и безынерционные. Инерционными называются элементы, характеристики которых зависят от скорости изменения переменных. Для таких элементов статические характеристики, определяющие зависимость между действующими значениями переменных, отличаются от динамических характеристик, устанавливающих взаимосвязь между мгновенными значениями переменных. Безынерционными называются элементы, характеристики которых не зависят от скорости изменения переменных. Для таких элементов статические и динамические характеристики совпадают.
Понятия инерционных и безынерционных элементов относительны: элемент может рассматриваться как безынерционный в допустимом (ограниченном сверху) диапазоне частот, при выходе за пределы которого он переходит в разряд инерционных.
В зависимости от вида характеристик различают нелинейные элементы с симметричными и несимметричными характеристиками. Симметричной называется характеристика, не зависящая от направления определяющих ее величин, т.е. имеющая симметрию относительно начала системы координат. Для несимметричной характеристики это условие не выполняется, т.е. Наличие у нелинейного элемента симметричной характеристики позволяет в целом ряде случаев упростить анализ схемы, осуществляя его в пределах одного квадранта.
По типу характеристики можно также разделить все нелинейные элементы на элементы с однозначной и неоднозначной характеристиками. Однозначной называется характеристика, у которой каждому значению х соответствует единственное значение y и наоборот. В случае неоднозначной характеристики каким-то значениям х может соответствовать два или более значения y или наоборот. У нелинейных резисторов неоднозначность характеристики обычно связана с наличием падающего участка, а у нелинейных индуктивных и емкостных элементов – с гистерезисом.
Наконец, все нелинейные элементы можно разделить на управляемые и неуправляемые. В отличие от неуправляемых управляемые нелинейные элементы (обычно трех- и многополюсники) содержат управляющие каналы, изменяя напряжение, ток, световой поток и др. в которых, изменяют их основные характеристики: вольт-амперную, вебер-амперную или кулон-вольтную.
В зависимости от вида составляющих нелинейных элементов, называют нелинейные цепи.
3. Коэффициент усиления нелинейного элемента
Рассмотрим нелинейный элемент (рис. 5). Подадим на вход нелинейного элемента гармонический сигнал с амплитудой – А0 и определим первую гармонику выходного сигнала.
При этом для входного и выходного сигналов можно записать следующие соотношения
(1)
где: – модуль вектора; – аргумент вектора.
Рассмотрим характеристику нелинейного элемента -, которая называется комплексным коэффициентом передачи нелинейного элемента. Эту характеристику можно строить в комплексной плоскости также, как и комплексный коэффициент передачи линейной части. При этом характеристика – зависит от частоты сигнала и не зависит от его амплитуды. Характеристика – зависит от амплитуды входного сигнала и не зависит от частоты, так как нелинейный элемент является безинерционным. Для однозначных характеристик его значения является действительными величинами, а для многозначных – комплексными.
Рассмотрим примеры построения комплексных коэффициентов передачи для наиболее характерных нелинейных элементов – .
1. Нелинейный элемент типа "усилитель с ограничением". Характеристики звена показаны на рис. 6. Подобными характеристиками обладают различного типа усилительные и исполнительные элементы автоматики (электронные, магнитные, пневматические, гидравлические и др.) в области больших входных сигналов.
Если амплитуда входного воздействия меньше а, то это обычное линейное безинерционное звено, при этом коэффициент усиления к является постоянной величиной. Фазовый сдвиг между входом и выходом равен нулю, поскольку характеристика нелинейного элемента является симметричной. По мере увеличения амплитуды – коэффициент усиления уменьшается. В некоторых методах исследования нелинейных систем используется характеристика обратного комплексного коэффициента передачи нелинейного элемента (-1/). Эта характеристика приведена на рис. 6.
Так как фазового сдвига между гармониками входного и выходного сигнала нет, то характеристика совпадает с вещественной осью.
Нелинейный элемент типа " зона нечувствительности ". Характеристики звена показаны на рис. 7. Подобными характеристиками обладают различного типа усилители в области малых входных сигналов.
Рис. 7
Если амплитуда входного сигнала расположена в пределах диапазона ± а, то выходной сигнал равен нулю в противном случае выходной сигнал равен не нулю, так как появляются вершины входной гармоники. Фазового сдвига нет. При больших амплитудах входного сигнала коэффициент усиления имеет постоянное значение, т. е. нелинейность не оказывает существенного влияния на выходной сигнал.
3. Нелинейный элемент типа " трехпозиционное реле без гистерезиса". Характеристики звена показаны на рис.8. Эта характеристика присуща релейным системам с обратной связью.
Так как характеристика однозначная, то фазового сдвига нет. Если амплитуда входного сигнала®¥, то выходной сигнал превращается в последовательность импульсов. При малых и больших амплитудах коэффициент k – мал.
Рис. 8
4. Нелинейный элемент типа "релейная характеристика". Характеристики звена показаны на (рис. 9).
Рис. 9
Первая гармоника будет сдвинута в сторону запаздывания. Величина фазового сдвига зависит от амплитуды входного сигнала и величины ± а.
Отношение амплитуд А1 /А0 при больших значениях амплитуды входного сигнала стремится к 0 , при этом фазовый сдвиг уменьшается. При малых амплитудах фазовый сдвиг равен 90°.
Если – вектор, то – обратный вектор.
5. Нелинейный элемент типа "люфт, зазор". Характеристики данного
нелинейного элемента приведены на рис. 10.
Модели нелинейных элементов. Модели нелинейных элементов могут быть реализованы путем включения в цепь операционного усилителя (на вход или в обратную связь) нелинейных двухполюсников. В зависимости от характеристик двухполюсника и способа его подключения можно реализовать любую нелинейную зависимость (рис. 11а, б, в).
Модели нелинейных звеньев широко используются при моделировании систем автоматического управления на ЭВМ.
1. Атабеков Г.И., Тимофеев А.Б., Купалян С.Д., Хухриков С.С. Теоретические основы электротехники (ТОЭ). Нелинейные электрические цепи. Электромагнитное поле. 5-е изд. Изд-во: ЛАНЬ, 2005. – 432с.
2. Бесекерский В.А., Попов Е.П. "Теория систем автоматического управления". Профессия, 2003 г. – 752с.
3. Гаврилов Нелинейные цепи в программах схемотехнического моделирования. Изд-во: СОЛОН-ПРЕСС, 2002. – 368с.
4. Дорф Р., Бишоп Р. Автоматика. Современные системы управления. 2002г. – 832с.
5. Сборник задач по теории автоматического регулирования и управления/ Под редакцией В. А. Бесекерского. — M.: Наука, 1978.
Читайте также:
- F 3.4. Характеристика объекта бизнеса организации
- I. Электрические характеристики
- I. Электрические характеристики
- II. Морфофункціональна характеристика відділів головного мозку
- III. Экономические и эксплуатационные характеристики
- III. Экономические и эксплуатационные характеристики
- L1.T3.1. Загальні характеристики аматрури.
- А.2. Характеристика теоретико-методологічних основ конфліктології
- Адміністративні (організаційно-розпорядчі) методи менеджменту, їх характеристика.
- Аміни, їх характеристика.
- Амінокислоти їх характеристика, властивості.
- Амплитудно-частотная характеристика
Тема АНАЛИЗ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ РЕЗИСТИВНЫМИ ЭЛЕМЕНТАМИ
Нелинейными электрическими элементами являются элементы, параметры которых зависят от тока и напряжения. Цепи, содержащие такие элементы, именуемые электрическими нелинейными цепями, обладают рядом новых свойств, которые отсутствуют у линейных цепей. Эти свойства позволяют создать основанные на них автоматические системы управления и регулирования, устройства для преобразования электромагнитной энергии, устройства для производства электрических измерений и передачи информации, быстродействующие вычислительные машины и т.д. Особенностью и сложностью анализа нелинейных систем является невозможность применения принципа наложения.
К нелинейным электрическим цепям постоянного тока относятся электрические цепи, содержащие нелинейные сопротивления, обладающие нелинейными вольт-амперными характеристиками, т.е. зависимость напряжения на зажимах резистивного нелинейного элемента от тока в нем задается его вольтамперной характеристикой (ВАХ).
Вольт-амперные характеристики могут быть заданы в виде графиков, таблиц и аналитических выражений.
В зависимости от вида характеристик различают следующие нелинейные элементы:
· с симметричной (относительно начала координат) и несимметричной характеристикой (рис. 10.1);


· однозначные и многозначные (рис. 10.2);
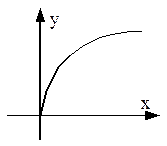
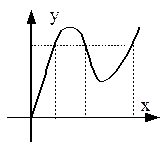


· управляемыми – имеющие семейство характеристик, каждая из которых определяется управляющим элементом а; неуправляемыми – имеющие только одну характеристику (рис. 10.4).
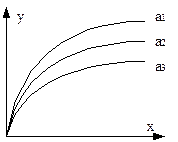
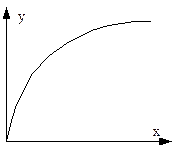
Статическими называют характеристики, в которых каждая точка дает значение постоянного напряжения при соответствующем значении постоянного тока. Из них определяют статическое сопротивление и статическую проводимость нелинейного элемента
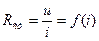 .
.
Электрическое состояние нелинейных цепей постоянного тока описывается системой алгебраических уравнений, составленных по первому и второму закону Кирхгофа. Общих аналитических методов решения нелинейных уравнений не существует, поэтому решение таких задач осуществляется численными методами с использованием ЭВМ. Однако существуют наиболее простые методы расчета цепей постоянного тока с резистивными элементами – графические и графоаналитические: метод эквивалентных преобразований и метод пересечения характеристик.
Метод эквивалентных преобразований для нелинейных цепей, так же как и для линейных, основан на замене нескольких элементов одним и сводится к нахождению ВАХ эквивалентного нелинейного элемента.
При расчете электрических цепей с последовательным или параллельным включением нелинейных (или линейных и нелинейных) сопротивлений их вольт-амперные характеристики представляются в общей координатной системе и по ним строится общая вольт-амперная характеристика всей нелинейной электрической цепи.
а) При последовательном соединении нелинейных резистивных элементов, графически заданных своими вольт-амперными характеристиками, по оси абсцисс которых откладываются напряжения, а по оси ординат – ток, складываются абсциссы этих кривых для различных значений тока. Абсцисса каждой точки эквивалентного элемента при заданном токе находится как сумма соответствующих падений напряжения на сопротивлениях, поскольку при последовательном соединении по сопротивлениям протекает один и тот же ток цепи (рис.4.5.).
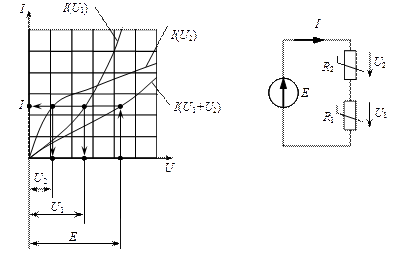
Рис.4.5. К расчету электрической цепи с последовательным соединением нелинейных элементов.
Таким образом, по общей вольт-амперной характеристике 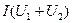 нелинейной цепи при заданном значении напряжения ЭДС легко определяют ток в нелинейной цепи I, а по заданному току, находят напряжение на каждом из последовательно соединенных сопротивлений, переходя к их вольт-амперным характеристикам.
нелинейной цепи при заданном значении напряжения ЭДС легко определяют ток в нелинейной цепи I, а по заданному току, находят напряжение на каждом из последовательно соединенных сопротивлений, переходя к их вольт-амперным характеристикам.
б) При параллельном соединении нелинейных резистивных элементов складываются ординаты ВАХ для различных значений напряжения. Ордината каждой точки вольт-амперной характеристики эквивалентного нелинейного сопротивления при заданном напряжении определяют как сумму токов в ветвях соответствующего сопротивления 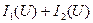 , так как при параллельном соединении на всех сопротивлениях действует одно и то же напряжение (рис.4.6).
, так как при параллельном соединении на всех сопротивлениях действует одно и то же напряжение (рис.4.6).
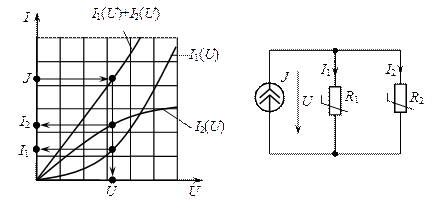
Рис.4.6. К расчету электрической цепи с параллельным соединением нелинейных элементов.
Следовательно, при параллельном включении сопротивлений, по общей ВАХ и заданном токе источника тока, нетрудно определить падение напряжения на параллельном участке цепи, а по известному напряжению, переходя к ВАХ каждого элемента, найти ток в каждом сопротивлении.
Применение графического метода расчёта цепей со смешанным соединением нелинейных резистивных элементов основано на методе свёртывания. Для получения характеристики всей цепи при смешанном соединении нелинейных элементов используются те же приемы, осуществляемые поочередно.
В методе пересечения характеристик реализуется графическое решение уравнения, определяющего электрическое состояние цепи при заданной величине источника.
а) При последовательном соединении линейного элемента и нелинейного резистивного элемента, графически заданного своей вольт-амперной характеристикой, решение задачи сводится к решению уравнения, составленного по второму закону Кирхгофа, и будет определяться точкой пересечения нагрузочной прямой с ВАХ нелинейного элемента. Для построения нагрузочной прямой, достаточно определить координаты двух точек, из опыта холостого хода и короткого замыкания. Напряжение холостого хода определяется по методу эквивалентного генератора. Точка пересечения линейной и нелинейной ВАХ получила название рабочей точки (рис.4.7.).
По второму закону Кирхгофа:
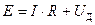 ,
,
При 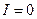 ,
, 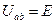 ;
;
при 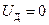 ,
, 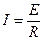 .
.
Таким образом, из графика находятся ток в цепи и напряжение на нелинейном элементе, что представляют собой координаты точки пересечения.
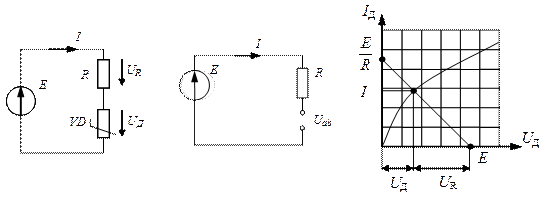


 Рис. 4.7 К расчету электрических цепей с последовательным включением нелинейного и линейного элементов методом пересечений.
Рис. 4.7 К расчету электрических цепей с последовательным включением нелинейного и линейного элементов методом пересечений.
б) При параллельном соединении линейного и нелинейного резистивного элемента, графически заданного своей вольт-амперной характеристикой, решение задачи сводится к решению уравнения, составленного по первому закону Кирхгофа, и будет определяться точкой пересечения нагрузочной прямой.
По первому закону Кирхгофа:
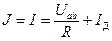 .
.
При 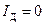 ,
, 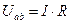 ;
;
При 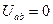 ,
, 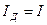 .
.
Координаты точки пересечения двух ВАХ линейной и нелинейной являются найденным решением задачи. Они определяют ток в нелинейном элементе и напряжение на нелинейном и линейном сопротивлении (рис.4.8.).
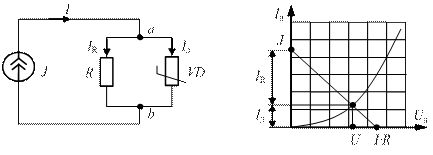
Рис. 4.8 К расчету электрических цепей с параллельным включением нелинейного и линейного элементов методом пересечений.
Пример. Нелинейные сопротивления R1 и R2, включенные последовательно в электрическую цепь постоянного тока (рис.4.9 а), имеют вольт-амперные характеристики I и II, приведенные на рис.4.9, б. Определить ток I в цепи и напряжения U1 и U2 на этих сопротивлениях, если приложенное к цепи напряжение U = 60 В. В каких пределах измениться напряжение ΔU цепи при изменении тока I от I1 = 25 мА до I2 = 175 мА.
Решение. Строят общую вольт-амперную характеристику III указанных двух последовательно соединенных нелинейных элементов (рис.4.9, б) исходя из условия, что подводимое к цепи напряжение U при данном токе I нагрузки равно сумме напряжений на сопротивлениях R1 и R2, т.е. U=U1+U2.
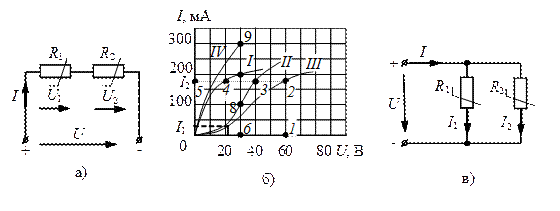
Рис.4.9. К расчету электрических цепей с включением нелинейных элементов
Ток в цепи при напряжении U = 60 В согласно зависимости III определяется ординатой 0 – 5, соответствующей I2 = 175 мА.
Напряжение на участках цепи находят из графических зависимостей. При токе I2 = 175 мА, U1 = 19 В (абсцисса 5-4), U2 = 41 В (абсцисса 5-3). При токе I1 = 25 мА напряжение, подводимое к цепи, U = 22 В. Следовательно, изменение подводимого к цепи напряжения при изменении тока в заданных пределах согласно рис. 4.9, б составляет: ΔU = 66 – 22 = 38 В.
| | | следующая лекция ==> | |
| Несимметричный режим работы трехфазной цепи | | | Тема МАГНИТНЫЕ ЦЕПИ |
Дата добавления: 2014-01-06 ; Просмотров: 870 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет