1) Поле однородно: В = const (рис. 8.22).
(5 выносится за знак интеграла, a |d/ для замкнутого контура равен нулю. Докажите это.)
Сила, действующая на ограниченное распределение тока во внешнем поле, равна нулю.
Однако на виток с током в однородном поле действует вращающий момент (рис. 8.23), стремящийся развернуть виток так, чтобы его магнитный момент стал параллельным полю:
Здесь in = IS п — магнитный момент витка. Если направление вектора in совпадает с направлением вектора В, момент сил равен нулю и это положение устойчиво; при отклонении in на угол а от положения равновесия возникает возвращающий момент М = |m|5sina.
Рис. 8.22 Рис. 8.23
Если других моментов сил нет или они малы, система будет совершать колебания (все видели, как колеблется стрелка компаса). Частота малых колебаний равна
где J — момент инерции системы.
2) Поле неоднородно (рис. 8.24). При совпадении направлений
векторов т и В появляется сила, втягивающая виток в область поля с большей индукцией. В общем случае можно показать, что сила, действующая на ограниченное распределение тока во внешнем поле, равна
Формула справедлива, если размеры распределения достаточно малы (в частности, если наш виток достаточно мал).
Задача 8.7. Виток с магнитным моментом т находится на расстоянии г от длинного прямого проводника. Виток и проводник лежат в одной плоскости (рис. 8.25). Найти силу, действующую на виток.
Виток притягивается к проводнику.
Но рассмотрим другую ситуацию: виток ориентирован иначе
(рис. 8.26). В этом случае т В = 0. Чему равна сила? Первая мысль — нулю. Но здесь нужна осторожность. Если функция в некоторой точке равна нулю, это не означает, что равна нулю производная.
Нужно выразить Вх и В как функции х, у:
Учитывая, что В = , получим
Рис. 8.26 Рис. 8.27
Пусть виток находится в точке (х, 0, 0). Из формулы (8.26) вид-
но, что в этой точке–=0, —
дуг) дхг ) г 1 2яг
Уже отмечалось, что формула (8.25) приближенная. Силу, действующую на прямоугольную рамку с током в поле прямого проводника (рис. 8.27), легко вычислить точно:
Видно, что при — « 1 формула (8.29) переходит в (8.27). г о
Если поместить в магнитное поле проводник с током, то между электронами, проходящими по проводнику, и внешним магнитным полем возникнут электромагнитные силы, которые, складываясь, образуют результирующую силу, стремящуюся вытолкнуть проводник из магнитного поля (рис.2.5).
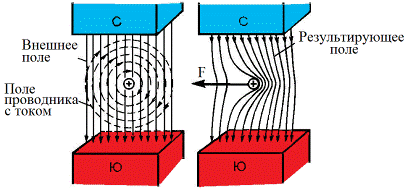
Рисунок 2.5. Выталкивание проводника с током из магнитного поля
С одной стороны будет наблюдаться сгущение магнитных линий, с противоположной стороны – разрежения.
Направление выталкивания проводника определяют по правилу левой руки(рис.2.6):
«Ладонь левой руки надо расположить так, чтобы силовые линии входили в нее, четыре вытянутых пальца совместить с направлением тока, тогда отогнутый большой палец укажет направление действия силы по выталкиванию проводника».
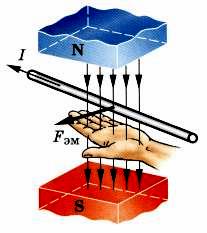
Рисунок 2.6. Определение направления выталкивания проводника с током магнитным потоком по правилу
Электромагнитная сила определяется законом Ампера:
«Электромагнитная сила, действующая на проводник с током, находящийся в магнитном поле и расположенный перпендикулярно направлению поля, равна произведению силы тока I, индукции магнитного поляВи длины проводникаℓ»: F=ВIℓ.
Если проводник расположен под углом αк силовым магнитным линиям, то: F=ВIℓsinα [Н], где: α угол между направлением проводника и направлением поля.
Виток с током в магнитном поле.
Поместим в магнитное поле не проводник, а виток (или катушку) и расположим его вертикально. Оказывается, выталкивания витка из магнитного поля не произойдёт. Если виток был помещён в магнитное поле так, как это показано на рис. 2.7 слева, то верхняя сторона его будет выталкиваться вправо, а нижняя – влево, т.е. электромагнитные силы, действующие на них, будут направлены в разные стороны. Возникает электромагнитный вращающий момент, который вызовет поворот витка. Виток будет поворачиваться, пока не займет горизонтальное положение, перпендикулярное магнитным силовым линиям поля, показанное на рис. 2.7 справа.
| Рисунок 2.7. Электромагнитные силы, действующие в магнитном поле на виток или катушку с током |
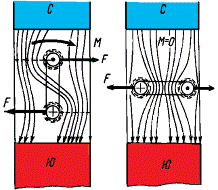
В этом положении произойдёт уравновешивание сил и виток останется неподвижным. Направление вращения витка определяется тоже по правилу левой руки.
1. Как располагаются магнитные силовые линии прямолинейного проводника с током?
2. Сформулируйте правило буравчика.
3. Назовите способы получения более сильных полей при небольших токах.
4. Как образуется результирующая сила проводника с током?
5. Сформулируйте правило левой руки.
6. Сформулируйте правило Ампера.
7. Что произойдёт с витком, если поместить его в магнитное поле?
8. Какая сила вызовет поворот витка?
2.3. Магнитные свойства веществ
Классификация ферромагнитных материалов.
Все вещества: твердые, жидкие и газообразные в зависимости от магнитных свойств делятся на:
· ферромагнитные: железо, никель, кобальт и их сплавы, обладают сильными магнитными свойствами; к магнитам притягиваются; стержни, изготовленные из них, устанавливаются вдоль магнитного поля; µотн=40-200000.
· парамагнитные: алюминий, олово, хром, марганец, платина, вольфрам, растворы солей железа и др.; слабо намагничиваются; слабее притягиваются к магнитам; стержни из них устанавливаются вдоль магнитного поля; µотн>1 (1,0037).
· диамагнитные: медь, серебро, золото, свинец, цинк, смола, вода, воздух и другие газы; от магнитов отталкиваются; стержни из них устанавливаются поперек поля; µотн
Дата добавления: 2016-04-22 ; просмотров: 2048 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Контур с током в магнитном поле.
Рассмотрим прямоугольную рамку с постоянным током 
в однородном магнитном поле (см. рис. 6.14).
Рис. 6.14. Прямоугольная рамка с током в магнитном поле:
а) вид сбоку, б) вид сверху
Рамка обладает дипольным магнитным моментом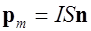 
, где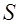 
площадь рамк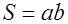и, 
, и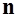 
– единичной нормаль к той же плоскости. Так как ток – постоянный, то величина дипольного момента 
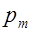не изменяется, но может изменяться направление вектора 
.
На боковые стороны рамки, согласно закону Ампера (см. (6.27)), действует пара сил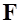 
, создающая вращательный момент силы 
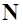. Механическая работа магнитных сил при повороте рамки на угол 
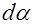равна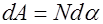 
, или, согласно (6.36), 
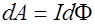. Магнитный поток через контур рамки 
, а величина его изменения при повороте на угол 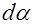составит 
.
Отсюда получим 
, то есть момент магнитной силы, действующий на рамку
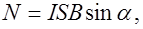
или в векторных обозначениях
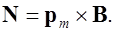(6.38)
Формула (6.38) оказывается справедлива и для магнитного диполя. Причем не только в однородном, но и в неоднородном поле, так как размер витка с током в этом случае пренебрежимо мал.
В однородном магнитном поле силы, действующие на боковые стороны рамки, одинаковы по величине, но противоположны по направлению. Аналогично компенсируют друг друга силы, действующие на верхнюю и нижнюю стороны рамки. Поэтому полная сила, действующая на рамку с током, как и на магнитный диполь, в однородном магнитном поле равна нулю.
Рис. 6.15 поясняет возникновение результирующей магнитной силы, действующей на виток с током в неоднородном магнитном поле.
На каждый элемент тока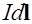 
витка действует магнитная сила 
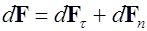, имеющая две компоненты – в плоскости витка и в направлении, перпендикулярном этой плоскости. Полная сила, действующая на виток, равна
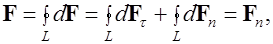
так как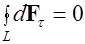 
из соображений симметрии.
Согласно рис. 6.15, сила, действующая на магнитный диполь в неоднородном магнитном поле, стремится втянуть диполь в область более сильного поля. Если направление тока в витке (направление вектора ) изменить на противоположное по сравнению с рис. 6.15, то магнитная сила будет стремиться вытолкнуть диполь в область более слабого поля.
Пусть в области, где находится магнитный диполь, нет внешних токов, создающих магнитное поле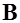 
. Тогда поле 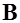в этой области – потенциальное. Работа 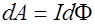, совершаемая магнитным полем над диполем, равна убыли его потенциальной энергии в магнитном поле. Так как ток – постоянный, то
где потенциальная энергия магнитного диполя
(6.39)
Сила, действующая на магнитный диполь со стороны неоднородного магнитного поля, равна
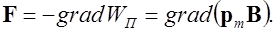(6.40)
Если дипольный момент – постоянный вектор, то выражение для силы упрощается (см. п. 1.11):
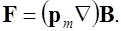(6.41)
Вывод: поведение магнитного диполя во внешнем магнитном поле подобно поведению электрического диполя во внешнем электрическом поле.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8845 – 
| 7556 – 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно