Взаимодействие двух постоянных магнитов

AM_System: Программа расчета осесимметричной магнитной системы из двух
соосных кольцевых постоянных магнитов с аксиальной намагниченностью

1. Конструкция магнитной системы из двух кольцевых магнитов

Конструкция осесимметричной магнитной системы из двух соосных кольцевых постоянных магнитов с аксиальной намагниченностью показана на рис. 1.1. Магнитная система состоит из двух соосно расположенных на некотором расстоянии друг от друга кольцевых или цилиндрических магнитов, намагниченных по оси. Направление намагниченности магнитов (вдоль оси симметрии) может быть одинаковым или противоположным друг другу.

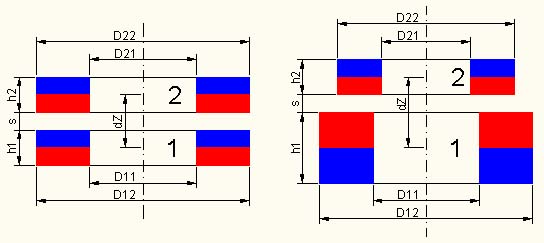
Рис. 1.1. Схема магнитной системы из двух кольцевых магнитов: слева – с одинаковым направлением намагниченности магнитов (например, калибровочная магнитная система), справа – с противоположным направлением намагниченности магнитов (например, магнитная опора). Северный полюс обозначен синим цветом, южный – красным.

Постоянный магнит 1 представляет собой кольцо (или цилиндр) внешним диаметром D12 высотой h 1 с отверстием диаметром D11 (или без отверстия).
Постоянный магнит 2 представляет собой кольцо (или цилиндр) внешним диаметром D22 высотой h 2 с отверстием диаметром D21 (или без отверстия).
Взаимное положение магнитов может быть определено либо расстоянием между ними s, либо расстоянием между их центрами dZ. Эти параметры связаны друг с другом следующим соотношением:

dZ = s + h 1/2 + h 2/2

Расстояние s между магнитами – это расстояние между верхним основанием магнита 1 и нижним основанием магнита 2. Величина s может принимать как положительные, так и отрицательные значения. Когда s ≥ 0, магнит 2 является верхним, а магнит 1 – нижним. Когда 0 > s > -( h 1 + h 2), один из магнитов находится частично внутри отверстия другого магнита. При этом должно выполняться соотношение для их диаметров: либо D22 ≤ D 11 (магнит 2 внутри магнита 1), либо D 12 ≤ D 21 (магнит 1 внутри магнита 2). Когда s ≤ -( h 1 + h 2), магнит 2 становится нижним, а магнит 1 – верхним.

Примеры осесимметричной магнитной системы из двух соосных кольцевых постоянных магнитов с аксиальной намагниченностью: калибровочная магнитная система [ 6 ] , аксиальный магнитный подшипник [ 8 ] , радиальный магнитный подшипник [ 8 ] .

Калибровочная магнитная система – система из двух одинаковых соосно расположенных кольцевых постоянных магнитов, намагниченность каждого из которых направлена в одну и ту же сторону вдоль оси системы. В центре системы имеется область однородного магнитного поля (зона однородности) с осевым направлением магнитной индукции. Размеры зоны однородности зависят от геометрических и физических параметров системы. Система может использоваться для калибровки датчиков магнитной индукции, обеспечивая их осевой и радиальный доступ к зоне однородности.

Аксиальный магнитный подшипник – осесимметричный подшипник, противодействующий осевой нагрузке и обеспечивающий свободное вращение объекта относительно оси. Принцип его работы основан на использовании сил отталкивания между соосными кольцевыми магнитами со встречной аксиальной намагниченностью. Аксиальный магнитный подшипник имеет радиальную неустойчивость, которую необходимо компенсировать дополнительными радиальными подшипниками (немагнитными). Разновидностью аксиального магнитного подшипника является магнитная опора, которая противодействует осевой нагрузке, создаваемой весом объекта.

Радиальный магнитный подшипник – осесимметричный подшипник, противодействующий радиальной нагрузке и обеспечивающий свободное вращение объекта относительно оси. Принцип его работы основан на использовании сил притяжения между соосными кольцевыми магнитами с аксиальной намагниченностью, направленной в одну и ту же сторону. Радиальный магнитный подшипник имеет аксиальную неустойчивость, которую необходимо компенсировать дополнительными аксиальными подшипниками (немагнитными).

Задача – по заданным геометрическим и физическим параметрам магнитной системы необходимо рассчитать магнитную индукцию создаваемого системой магнитного поля и силу взаимодействия постоянных магнитов.

2. Расчет индукции магнитного поля одиночного постоянного кольцевого (цилиндрического) магнита

Цилиндрический постоянный магнит с аксиальным направлением намагниченности можно рассматривать как однослойный соленоид с бесконечно тонкой обмоткой, геометрически соответствующей боковой поверхности магнита, по которой течет намагничивающий ток I (рис. 2.1).

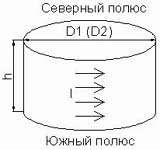
Рис. 2.1. Представление цилиндрического постоянного магнита с осевой намагниченностью эквивалентным соленоидом.

Условием эквивалентности магнита и соленоида является равенство их магнитных моментов. Магнитный момент магнита P может быть найден по формуле:

P = M V = M S h, где M – намагниченность магнита, V – его объем, S – площадь сечения, h – высота.

Магнитный момент эквивалентного соленоида:

P = j h S , где j = I / h – линейная плотность намагничивающего тока.

Для материалов с прямоугольной петлей гистерезиса (феррит бария, феррит стронция, неодим-железо-бор, самарий-кобальт и т. п.):

Br / m ₀, где Br – остаточная индукция, m ₀ = 4 p ∙ 10 -7 Гн/м – магнитная постоянная. Таким образом, линейную плотность намагничивающего тока можно выразить приближенной формулой:

Кольцевой постоянный магнит с аксиальным направлением намагниченности может быть представлен как два однослойных цилиндрических соленоида с бесконечно тонкой обмоткой, вложенных друг в друга. Соленоид диаметром D 2 и высотой h соответствует внешней боковой поверхности магнита, а соленоид диаметром D 1 и высотой h – внутренней поверхности отверстия. Намагничивающие токи в соленоидах равны по величине и противоположны по направлению.

Величину и направление вектора магнитной индукции d B в произвольной точке магнитного поля, создаваемого в вакууме (или воздухе) элементом проводника длиной dl с током I , можно найти с помощью закона Био – Савара – Лапласа [ 4 ] :

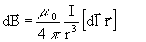
где d l – вектор элемента проводника, численно равный dl и проведенный в направлении тока, r – радиус-вектор, проведенный из этого элемента проводника в рассматриваемую точку поля, r = mod ( r ). Этот принцип расчета положен в основу программы A_Magnet [1]. Ее алгоритмы и формулы для расчета магнитной индукции использованы в программе AM_System.

3. Расчет магнитной индукции системы из двух кольцевых магнитов

Для расчетов систем с осевой симметрией предпочтительнее использовать систему цилиндрических координат. Центр системы координат в данном случае удобно поместить на оси магнитной системы посередине между магнитами (рис. 3.1), т. е. на расстоянии по s/2 как от верхнего основания магнита 1, так и от нижнего основания магнита 2. Необходимо помнить (см. п. 1), что величина s может принимать как положительные, так и отрицательные значения. Когда s ≥ 0, магнит 2 является верхним, а магнит 1 – нижним. Когда 0 > s > -( h 1 + h 2), один из магнитов находится частично внутри отверстия другого магнита. При этом должно выполняться соотношение для их диаметров: либо D22 ≤ D 11 (магнит 2 внутри магнита 1), либо D 12 ≤ D 21 (магнит 1 внутри магнита 2). Когда s ≤ -( h 1 + h 2), магнит 2 становится нижним, а магнит 1 – верхним.

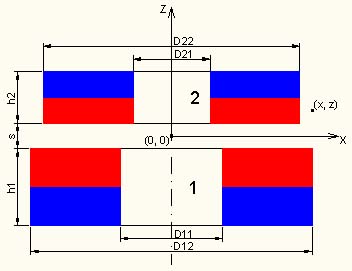
Рис. 3.1. Схема магнитной системы из двух кольцевых магнитов: центр координат – на оси системы посередине между магнитами, X – радиальная координата, Z – аксиальная координата.

Так как магнитная система состоит из двух магнитов, то в соответствии с принципом суперпозиции ее магнитное поле равно сумме магнитных полей магнитов [4] . Введем следующие обозначения. Магнитная индукция магнита 1 имеет радиальную B1 x ( x , 0, z ) и аксиальную B 1 z ( x , 0, z ) составляющие (рассчитываемые по закону Био-Савара-Лапласа относительно центра магнита 1 с остаточной индукцией Br 1). Магнитная индукция магнита 2 имеет радиальную B2 x ( x , 0, z ) и аксиальную B 2 z ( x , 0, z ) составляющие (рассчитываемые по закону Био-Савара-Лапласа относительно центра магнита 2 с остаточной индукцией Br 2). Магнитная индукция B12 (x, 0, z) магнитной системы имеет радиальную B12x (x, 0, z) и аксиальную B12z ( x , 0, z ) составляющие, рассчитываемые относительно центра опоры с учетом того, что магниты находятся на расстоянии s друг от друга по формулам:

B12x (x, 0, z) = B1x (x, 0, z + h1/2 + s/2) + B2x (x, 0, z – h2/2 – s/2)

B12z (x, 0, z) = B1z (x, 0, z + h1/2 + s/2) + B2z (x, 0, z – h2/2 – s/2)

Модуль магнитной индукции системы B12 (x, 0, z):

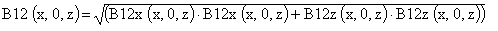
4. Расчет силы взаимодействия магнитов

Для расчета силы взаимодействия (притяжения или отталкивания) магнитов предположим, что магнитное поле магнита 1 с радиальной B1 x ( x , 0, z ) и аксиальной B 1 z ( x , 0, z ) составляющими магнитной индукции (рассчитываемыми по закону Био-Савара-Лапласа относительно центра магнита 1) действует на эквивалентные соленоиды с линейной плотностью тока j 2 = + Br 2/ m ₀ , заменяющие магнит 2, создавая силу Ампера (сила Ампера – сила, действующая со стороны магнитного поля на проводник с током) [4] . Элементарная сила Ампера dF , действующая на малый элемент dl длины проводника, по которому идет электрический ток I , равна:

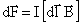
где dl – вектор, численно равный длине dl элемента проводника и направленный в ту же сторону, что и вектор j плотности тока в этом элементе проводника.

Если векторы dl и B взаимно перпендикулярны, то направление силы dF можно найти по правилу левой руки: если ладонь левой руки расположить так, чтобы вектор магнитной индукции входил в ладонь, а четыре вытянутых пальца указывали бы направление электрического тока, то отставленный большой палец укажет направление силы, действующей со стороны поля на проводник.

Сила Ампера, возникающая за счет аксиальной компоненты магнитной индукции поля магнита, имеет только радиальную составляющую. Ее воздействие на соленоид сводится к его радиальному сжатию (растяжению). Таким образом, искомая сила определяется только радиальной компонентой B 1 x индукции магнитного поля постоянного магнита 1. Причем радиальная компонента индукции магнитного поля постоянного магнита 1 и вектора линейной плотности тока j2 в эквивалентной магниту 2 системе соленоидов взаимно перпендикулярны.

Линейная плотность тока в эквивалентной магниту 2 системе соленоидов:

j 2 ( D 22/2, 0, z) = Br 2/ m ₀ для наружного соленоида диаметром D22

j 2 ( D 21/2, 0, z ) = – Br 2/ m ₀ для внутреннего соленоида диаметром D21

Тогда для элементарной силы Ампера d 2 F можно записать:

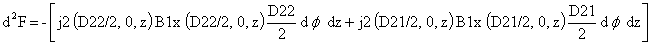
где (D22/2) d f и (D21/2) d f – элементы длины проводника обмотки в цилиндрической системе координат.

Или, с учетом осевой симметрии системы:

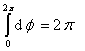
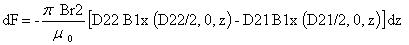
С учетом положения центра координат пределы интегрирования по z будут от s/2 до s /2 + h2, а радиальную составляющую магнитной индукции магнита 1 B 1 x , рассчитанную по формулам п. 2 относительно его центра, надо брать в точках (D22/2, 0, z + h 1/2 + s /2) и ( D 21/2, 0, z + h 1/2 + s /2), т. е. относительно центра координат магнитной опоры:

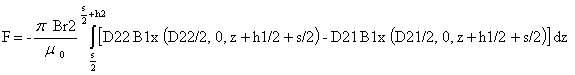
5. Программа Axial Magnetic System версия 1.0

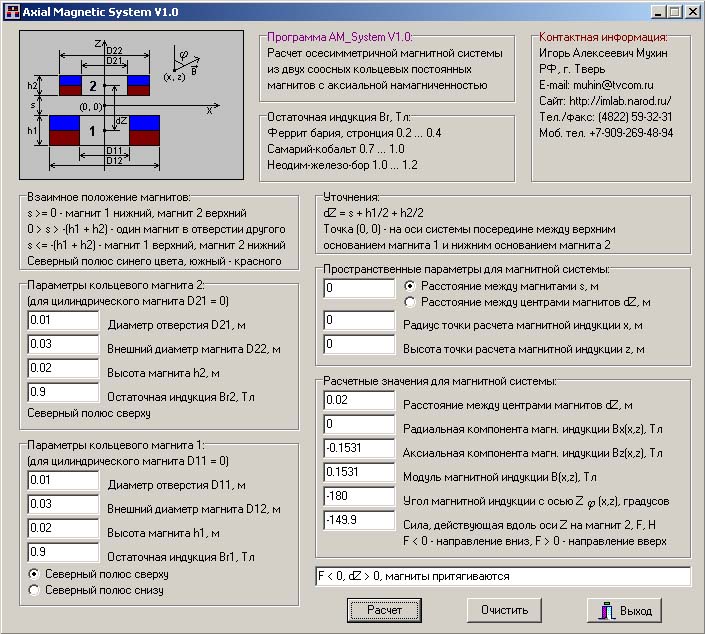
Рис. 5.1. Внешний вид окна программы Axial Magnetic System V 1.0.

D 21 – диаметр отверстия в постоянном магните 2, м
D 22 – внешний диаметр постоянного магнита 2, м
h 2 – высота постоянного магнита 2, м
Br 2 – остаточная индукция материала постоянного магнита 2, Тл
Северный полюс магнита 2 находится сверху
D 11 – диаметр отверстия в постоянном магните 1, м
D 12 – внешний диаметр постоянного магнита 1, м
h 1 – высота постоянного магнита 1, м
Br 1 – остаточная индукция материала постоянного магнита 1, Тл
Положение северного полюса магнита 1 (сверху или снизу) выбирается
В зависимости от предпочтения выбирается один из двух пространственных параметров, характеризующих взаимное положение магнитов:
Либо s – расстояние между верхним основанием магнита 1 и нижним основанием магнита 2, м (величина s может быть как положительной, так и отрицательной)
Либо dZ – расстояние между центрами магнитов 1 и 2, м (величина dZ может быть как положительной, так и отрицательной)
x – радиус точки расчета магнитной индукции относительно начала координат (0, 0), м
z – высота точки расчета магнитной индукции относительно начала координат (0, 0), м

Программа производит проверку входных данных на физическую и математическую корректность, а также их совместимость друг с другом.

В зависимости от выбранного пространственного параметра, характеризующего взаимное положение магнитов рассчитывается:
Либо s – расстояние между верхним основанием магнита 1 и нижним основанием магнита 2, м
Либо dZ – расстояние между центрами магнитов 1 и 2, м
Bx ( x , z ) – радиальная компонента магнитной индукции системы в точке (x, z), Тл
Bz ( x , z ) – аксиальная компонента магнитной индукции системы в точке (x, z), Тл
B( x , z ) – величина модуля магнитной индукции системы в точке (x, z), Тл
f (x, z) – угол между направлением вектора магнитной индукции и осью Z, градусов
F – сила, действующая на магнит 2 со стороны магнита 1, Н. Положительное значение силы означает, что она направлена вдоль оси Z вверх, отрицательное – в противоположном направлении (вниз). Если центр магнита 2 находится выше центра магнита 1 (dZ > 0), то отрицательное значение силы (F 0) – что отталкиваются. Если центр магнита 2 находится ниже центра магнита 1 (dZ Z , а положительное (F > 0) – что притягиваются. Когда центры магнитов совпадают (dZ = 0), магниты вдоль оси Z не взаимодействуют. Ненулевое значение силы в данном случае обусловлено погрешностью расчета.

Расчеты производятся в системе СИ. Результаты выводятся на экран монитора.

После запуска программы можно вводить входные данные и производить расчет нажатием кнопки "Расчет". Входные данные ( D 11, D 12, h 1, Br 1, D 21, D 22, h 2, Br 2, s , dZ , x , z ) необходимо вводить, учитывая принятый в операционной системе (ОС) формат разделителя для десятичной дроби – точка или запятая, например, 0.005 или 0,005, либо установите в ОС точку в качестве разделителя. Также при вводе или при выводе может использоваться экспоненциальный формат X . XXEY , где латинская буква E обозначает основание 10, а Y – степень (например, 1.67E-8 = 1.67 ∙ 10 -8 = 0.0000000167).

Для очистки окон с выходными данными следует нажать кнопку "Очистить". Для того, чтобы закрыть программу, следует нажать кнопку "Выход".

6 . Демонстрационная версия программы A M_ System

Демонстрационная версия программы позволяет рассчитывать параметры магнитной системы только при нулевом расстоянии между магнитами (s = 0) . Магнитная индукция рассчитывается только в точках, лежащих на оси симметрии системы ( x = 0 ). Время одного расчета может составлять до нескольких секунд при использовании компьютера с процессором Pentium-I 200 МГц или аналогичным. Программа может работать с операционными системами (ОС) Windows 95, 98 и XP (с другими ОС семейства Windows не проверялась).

Файл A M_ System1 0d.rar необходимо распаковать в заранее созданную папку. Упаковка производилась с помощью WinR AR 3 . 6 0. Результат распаковки: A M_ System 10d.exe – исполняемый файл программы. Для удобства запуска можно создать значок программы на рабочем столе. После запуска программы можно вводить входные данные в системе СИ и производить расчет нажатием соответствующей кнопки. Проверить правильность расчетов можно по внешнему виду окна программы, приведенному на рис. 5.1.

Скопированные файлы желательно проверить на отсутствие вирусного кода в режиме on-line [1 0 ].

По вопросу получения полной версии программы обращайтесь к автору (см. раздел Контактная информация ).

Ссылки:

1. A_Magnet: Программа-калькулятор индукции магнитного поля кольцевого (цилиндрического) магнита методом эквивалентного соленоида
2. Выгодский М. Я. Справочник по высшей математике. – М.: Издательство " Наука " , гл. ред. физ.-мат. лит., 1977. – 872 с.; ил.
3. Двайт Г. Б. Таблицы интегралов и другие математические формулы. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 176 с.
4. Законы и уравнения магнитного поля
5. Иродов И. Е. Основные законы электромагнетизма: Учеб. пособие для студентов вузов. – 2-е, стереотип. – М.: Высш. шк., 1991. – 288 с.: ил.
6. Калибровочная магнитная система из двух соосно расположенных кольцевых постоянных магнитов с зоной однородности в центре
7. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Издательство " Наука " , гл. ред. физ.-мат. лит., 1968 г. – 720 с .; ил .
8. Пассивные магнитные подшипники (подвесы) на постоянных магнитах
9. Постоянные магниты: Справочник / Альтман А. Б., Герберг А. Н., Гладышев П. А. и др.; Под ред. Ю. М. Пятина. – 2-е изд., перераб. и доп. – М.: Энергия, 1980. – 488 с., ил.
10. Проверка файлов пользователя на наличие вирусного кода в режиме on-line
11. Физические величины: Справочник / А. П. Бабичев, Н. А. Бабушкина, А. М. Братковский и др.; Под. ред. И. С. Григорьева, Е. З. Мейлихова. – М.; Энергоатомиздат, 1991. – 1232 с.
12. Яворский Б. М., Детлаф А. А. Справочник по физике / Для инженеров и студентов вузов. – 7 изд., испр. – М.: Издательство "Наука", Гл. ред. физ.-мат лит., 1978. – 944 с.; ил.

• Аксиальный подшипник – осесимметричный подшипник, создающий противодействие продольным (осевым) нагрузкам.
• Магнитная индукция – вектор, численно равный пределу отношения силы, действующей со стороны магнитного поля на элемент проводника с электрическим током, к произведению тока и длины элемента проводника, если длина этого элемента стремится к нулю, а элемент так расположен в поле, что этот предел имеет наибольшее значение, и направленный перпендикулярно к направлению элемента проводника и к направлению силы, действующей на этот элемент со стороны магнитного поля, причем из его конца вращение по кратчайшему расстоянию от направления силы к направлению тока в элементе проводника должно быть видно происходящим против часовой стрелки.
• Магнитное поле – разновидность электромагнитного поля, создаваемая движущимися электрическими зарядами или токами и оказывающая силовое воздействие на движущиеся электрические заряды или токи.
• Магнитный подшипник – подшипник, принцип работы которого основан на использовании сил магнитного притяжения или отталкивания.
• Намагниченность – магнитный момент единицы объема .
• Операционная система (англ. operating system) – базовый набор программ, обеспечивающий работу компьютера и его взаимодействие с пользователем.
• Остаточная индукция – величина магнитной индукции, сохраняющейся в образце после уменьшения напряженности внешнего поля до нуля.
• Постоянный магнит – объект, создающий магнитное поле за счет собственных внутренних элементарных электрических токов, текущих без использования внешнего источника энергии в составляющем объект материале.
• Принцип суперпозиции магнитных полей – магнитное поле, создаваемое несколькими движущимися зарядами или токами, равно векторной сумме магнитных полей, создаваемых каждым зарядом или током в отдельности.
• Радиальный подшипник – осесимметричный подшипник, создающий противодействие поперечным (радиальным) нагрузкам.

Одно из наиболее часто встречающихся в обычной жизни проявлений магнитного поля — взаимодействие двух магнитов: одинаковые полюса отталкиваются, противоположные притягиваются. Представляется заманчивым описать взаимодействие между магнитами как взаимодействие между двумя монополями, и с формальной точки зрения эта идея вполне реализуема и часто весьма удобна, а значит практически полезна (в расчётах); однако детальный анализ показывает, что на самом деле это не полностью правильное описание явления (наиболее очевидным вопросом, не получающим объяснения в рамках такой модели, является вопрос о том, почему монополи никогда не могут быть разделены, то есть почему эксперимент показывает, что никакое изолированное тело на самом деле не обладает магнитным зарядом; кроме того, слабостью модели является то, что она неприменима к магнитному полю, создаваемому макроскопическим током, а значит, если не рассматривать её как чисто формальный приём, приводит лишь к усложнению теории в фундаментальном смысле).

Правильнее будет сказать, что на магнитный диполь, помещённый в неоднородное поле, действует сила, которая стремится повернуть его так, чтобы магнитный момент диполя был сонаправлен с магнитным полем. Но никакой магнит не испытывает действия (суммарной) силы со стороны однородного магнитного поля. Сила, действующая на магнитный диполь с магнитным моментом m выражается по формуле:

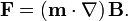
Сила, действующая на магнит (не являющийся одиночным точечным диполем) со стороны неоднородного магнитного поля, может быть определена суммированием всех сил (определяемых данной формулой), действующих на элементарные диполи, составляющие магнит. Впрочем, возможен подход, сводящий взаимодействие магнитов к силе Ампера, а сама формула выше для силы, действующей на магнитный диполь, тоже может быть получена, исходя из силы Ампера.

Вернуться на главную страницу. или ЗАКАЗАТЬ РАБОТУ

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Постоянный магнит.

Постоянный магнит — это изделие из материала, который является автономным (изолированным, самостоятельным) источником постоянного магнитного поля.

Природные (естественные) магниты.

Магнитные свойства некоторых природных минералов были известны еще в древности. Так, найдены письменные свидетельства более чем 2000-летней давности о том, что в древнем Китае использовались естественные постоянные магниты в качестве компасов. О притяжении и отталкивании магнитов и намагничивании ими железных опилок есть упоминания в трудах древнегреческих и римских ученых (например, поэма «О природе вещей» Лукреция Кара).

Природные магниты являются кусками магнитного железняка (магнетита), который состоит из FeO (31 %) и Fe₂O (69 %). Поднеся такой кусок минерала к мелким железным пред­метам — гвоздям, опилкам, тонкому лезвию и т. д., он их притянет.

Искусственные постоянные магниты.

Искусственные постоянные магниты изготавливаются из специальных сплавов, включающие в себя железо, никель, кобальт и другие. Эти металлы намагничива­ются (приобретают магнитные свойства), если их поднести к постоянным магнитам. Поэтому, чтобы сделать из них постоянные магниты, их специально держат в сильных магнитных полях, после этого они сами становятся источниками постоянного магнитного поля и могут долгое время сохранять в себе магнитные свойства.

На рисунке выше изображены дугообразный и полосовой магниты.

На рисунке выше кар­тины магнитных полей этих магнитов, полученных методом, который впервые применил в сво­их исследованиях М. Фарадей: при помощи железных опилок, рассыпанных на листе бумаги, на котором лежит магнит. Каждый магнит имеет 2 полюса — места наибольшего сгущения магнитных силовых линий (их называют также линиями магнитного поля, либо линиями магнитной индукции поля). Это места, к которым больше всего притягиваются железные опилки.

Один из полюсов называется северным (N), другой — южным (S). Поднеся 2 магнита друг к другу одноименными полюсами, будет видно, что они отталкиваются, а если разноименными — притягиваются.

На рисунке четко видно, что магнитные линии магнита — замкнутые линии (точно такие, как магнитные линии магнитного поля постоянного тока). На рисунке ниже показаны силовые линии магнитного поля 2х магнитов, обращенных друг к другу одноименными и разноименными полюсами.

Центральная часть этих изображений напоминает картины электрических полей 2х зарядов (разноименных и одноименных). Но существенным различием электрического и магнитного полей является то, что линии электрического поля начинаются на зарядах и заканчи­ваются на них. Магнитных же зарядов в природе не существует. Линии магнитного поля выходят из северного полюса магнита и входят в южный, они продолжаются и в теле магнита, то есть, как было сказано выше, являются замкнутыми линиями. Поля, силовые линии которых замкнуты, называются вихревыми. Магнитное поле — это вихревое поле (в этом его отличие от электрического).

Применение магнитов.

Самым древним магнитным прибором является всем хорошо известный компас. В современ­ной технике магниты используются очень широко: в электродвигателях, в радиотехнике, в электроизмерительной аппаратуре и т. д.