Зависимость магнитной индукции от напряженности магнитного поля

1. Вращающий момент, действующий на рамку с током со стороны магнитного поля. Магнитный момент рамки с током. Вращающий момент. Определение индукции магнитного поля. Единицы индукции и вращающего момента.

Поместив рамку в однородное магнитное поле, на нее действует пара сил, которая создает вращающий момент.

2. Напряженность магнитного поля и ее связь с индукцией. Единица напряженности.

Вектор магнитной индукции является общей характеристикой точек магнитного поля независимо от того, как создается магнитное поле: намагниченным телом или проводником с током находящимся в данной среде.

Однако можно ввести некоторую характеристику магнитного поля не зависящую от среды, а определяющуюся токами и конфигурацией проводников – вектор напряженности магнитного поля. Эти две характеристики (одна общая, а другая частная) связаны между собой: 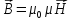где 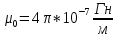– абсолютная магнитная проницаемость вакуума,μ — относительная магнитная проницаемость среды, для вакуума μ = 1.

Напряженностью магнитного поля – отношение механической силы, действующей на положительный полюс пробного магнита, к величине его магнитной массы или механическая сила, действующая на положительный полюс пробного магнита единичной массы в данной точке поля.

Единица напряженности магнитного поля — ампер на метр (А/м): 1 А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4π*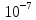Тл.

3. Изображение магнитных полей с помощью силовых линий индукции (напряженности). Вид линий магнитной индукции прямого и кругового токов, соленоида. Правила, но которым определяют направление линий магнитной индукции.

4. Магнитные поля проводников с токами. Закон Био-Савара-Лапласа.

Магнитное поле – это силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения.

В векторной форме: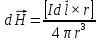

В скалярной форме: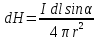

5. Применение закона Био-Савара-Лапласа для определения напряженности поля, создаваемого:

а) прямым проводником конечной длины (вывод формулы)

б) бесконечно длинным прямым проводником (вывод формулы)

в) круговым проводником в центре (вывод формулы)

г) соленоидом и тороидом

д) круговым проводником на оси (без вывода)

6. Сила Ампера. Правило для определения направления силы Ампера.

На проводник с током, находящийся в магнитном поле, действует сила, равная F = I·L·B·sina

I – сила тока в проводнике; B – модуль вектора индукции магнитного поля; L – длина проводника, находящегося в магнитном поле; a – угол между вектором магнитного поля инаправлением тока в проводнике.

Сила Ампера – Сила, действующую на проводник с током в магнитном поле.

Максимальная сила Ампера равна: F = I·L·B. Ей соответствует a = 90.

Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая вектора магнитной индукции В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующей на отрезок проводника с током, то есть силы Ампера.

Определение. Магнетики, магнитная проницаемость которых достигает больших значений и зависит от внешнего магнитного поля и предшествующей истории, называются ферромагнетиками.

К их числу, например, относятся железо, никель, кобальт, их сплавы и соединения в кристаллическом состоянии. Намагниченность ферромагнетиков до 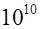раз может превышать намагниченность пара- или диамагнетиков.

Кривая намагничивания и петлягистерезиса. Магнитная восприимчивость ферромагнетиков зависит от напряженности магнитного поля. График нелинейной зависимости намагниченности 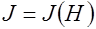от напряженности поля показан на рис. 7.11, а.

При увеличении напряженности поля намагниченность испытывает насыщение: 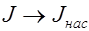при .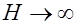

График нелинейной зависимости индукции 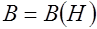от напряженности магнитного поля называется кривой намагниченности (см. рис. 7.11, б).

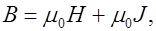
то кривая намагниченности не выходит на насыщение.

Если производить перемагничивание образца в периодическом магнитном поле, то, по аналогии с сегнетоэлектриками, кривая зависимости 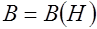имеет вид петли гистерезиса (см. рис. 7.12). Для наблюдения гистерезиса достаточно поместить ферромагнитный сердечник внутрь соленоида, по которому пропускать периодически изменяющийся электрический ток.

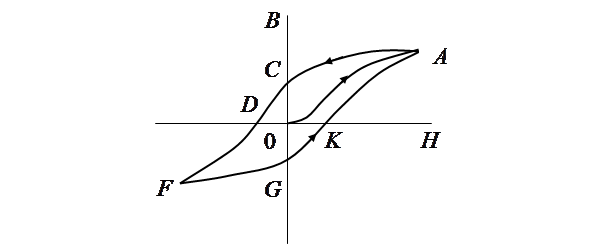
Кривая 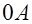– кривая намагничивания из начального размагниченного состояния. Петля гистерезиса – замкнутая кривая 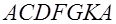. При уменьшении напряженности поля от максимального значения в положении 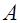до нуля изменение индукции магнитного поля запаздывает относительно кривой намагничивания 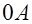. Это указывает на зависимость текущих значений индукции не только от значений напряженности поля в тот же момент, но и от значений напряженности в предшествующие моменты.

Вывод. Ферромагнетики обладают памятью.

При 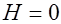сохраняется остаточное намагничение. Индукция, соответствующая отрезку 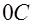, называется остаточной. Ферромагнетик в этом состоянии становится постоянным магнитом, если разомкнуть цепь обмотки соленоида в момент, когда сила тока в обмотке, уменьшаясь, станет равной нулю. Для полного размагничивания ферромагнетика (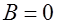) надо приложить внешнее магнитное поле обратного направления с напряженностью, соответствующей отрезку . Эта напряженность называется коорцетивной силой ферромагнетика.

Форма петли гистерезиса, остаточная индукция и коорцетивная сила зависят от материала.

Классификация ферромагнитных материалов. Ферромагнитные материалы делят на две группы:

а) мягкие ферромагнетики с большой магнитной проницаемостью с малой коорцетивной силой, то есть легко намагничивающиеся и размагничивающиеся;

б) жесткие ферромагнетики с относительно низкой магнитной проницаемостью, но большой коорцетивной силой, то есть трудно намагничивающиеся и размагничивающиеся.

Материалы первой группы используют в электротехнике переменного тока, например, как сердечники трансформаторов, а второй группы – для создания постоянных магнитов.

Кривая магнитной проницаемости. Эта кривая представляет собой график зависимости магнитной проницаемости ферромагнетика от напряженности магнитного поля: 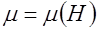. Впервые была построена экспериментально Столетовым, который изучал намагничение ферромагнетиков. Ее характерный вид показан на рис. 7.13, и она может быть построена на основе кривой намагничивания.

С ростом напряженности значение 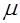достигает максимума, а затем, при достижении насыщения намагниченности, быстро падает. На практике в максимуме магнитная проницаемость может достигать значений .

Взаимодействие электронов. Последовательное описание ферромагнетизма как явления, обусловленного взаимодействием спиновых моментов электронов, дается лишь в квантовой, а не в классической теории. Ферромагнетики обладают свойством спонтанной (самопроизвольной) намагниченности. То есть, в отсутствии внешнего магнитного поля спины электронов образца взаимодействуют друг с другом так, что стремятся ориентироваться в одном направлении. Это взаимодействие спинов имеет квантовую природу и называется обменным. Электроны, как частицы с полуцелым спином, подчиняются квантовой статистике Ферми-Дирака, которая не допускает нахождения двух частиц в одном состоянии. Поэтому электроны с параллельными спинами раздвигаются в пространстве, что уменьшает потенциальную энергию их кулоновского взаимодействия. Энергией обменного взаимодействия называется разность энергий систем, образованных парами электронов с антипараллельными и параллельными спинами.

Видно, что конфигурация электронов с параллельными спинами энергетически наиболее выгодна, так как обладает наименьшим запасом потенциальной энергии. Более того, для возникновения ферромагнетизма требуется, чтобы уменьшение потенциальной энергии взаимодействия электронов за счет достижения согласованной ориентации спинов было больше, чем увеличение кинетической энергии электронов, происходящее при этом.

Каждая область с согласованной ориентацией спинов образует домен, как область самопроизвольной намагниченности. В отсутствии внешнего магнитного поля рост объема каждого домена в образце ограничивается увеличением запаса потенциальной энергии его поверхностного слоя. В силу теплового движения направления спинов электронов в разных доменах ориентированы хаотически друг по отношению к другу. Поэтому в целом образец размагничен.

В элементарной теории ферромагнетизма доказывается, что магнитная восприимчивость материала ферромагнетика без учета обменного взаимодействия оказывается такой же, как и у парамагнетика:

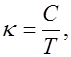
где 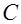соответствует постоянной Кюри.

Учет обменного взаимодействия позволяет получить магнитную восприимчивость ферромагнетика:

(7.32)

где 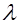– постоянная обменного взаимодействия, зависящая от рода материала.

В области температур 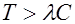материал ведет себя как парамагнетик – магнитная восприимчивость падает с ростом температуры. С уменьшением температуры, при 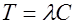, имеем: 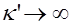, что означает возникновение конечной по величине намагниченности при сколь угодно малом внешнем поле. То есть, скачкообразно возникает спонтанная намагниченность при фазовом переходе второго рода образца из парамагнитного в ферромагнитное состояние. Более точная теория дает конечный по величине скачок восприимчивости при том же фазовом переходе. При дальнейшем уменьшении температуры, когда , восприимчивость продолжает расти, но скорость ее нарастания падает. При этом материал находится в ферромагнитной фазе.

Закон Кюри-Вейсса. Согласно (7.32), для всякого ферромагнетика существует температура Кюри-Вейсса, равная 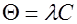. Приблизительно при этой температуре происходит фазовый переход между парамагнитной и ферромагнитной фазой образца.

Перемагничивание. При росте напряженности намагничивающего поля сначала происходит обратимое смещение границ доменов и повороты граничных стенок. Увеличиваются размеры доменов, у которых проекция вектора намагниченности на направление вектора напряженности поля положительна. Соответственно размеры остальных доменов образца уменьшаются (см. рис. 7.14).

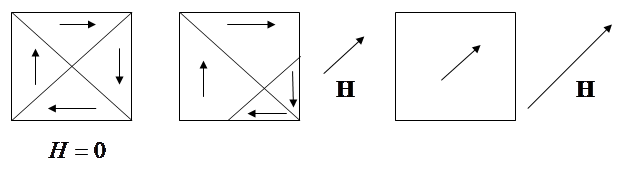
При дальнейшем увеличении напряженности поля смещение границ доменов становится необратимым и происходит переориентация намагниченности еще сохранившихся доменов образца в направлении вектора . В результате образец состоит из одного домена с ориентацией намагниченности вдоль , что соответствует достижению насыщения намагниченности.

Антиферромагнетизм. При определенных условиях обменное взаимодействие таково, что минимум энергии взаимодействия спиновых моментов соседних атомов достигается при антипараллельной ориентации этих спинов. Происходит формирование двух структур (подрешеток) спиновых моментов. Каждая из них спонтанно намагничена (см. рис. 7.15). Подрешетки намагничены с одинаковой интенсивностью, но в противоположных направлениях. Суммарная намагниченность равна нулю. Изученная ситуация соответствует антиферромагнетизму. Примерами антиферромагнетиков служат хром и марганец. Антиферромагнетики имеют очень малую магнитную восприимчивость и ведут себя подобно слабым парамагнетикам (ср. с (7.32)):

(7.33)

где 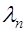– постоянная обменного взаимодействия антиферромагнетика.

С падением температуры, как и у ферромагнетиков, происходит фазовый переход – приближенно при температуре Кюри-Вейсса , и вещество скачкообразно переходит из парамагнитной в антиферромагнитную фазу.

Ферримагнетизмимеет место, если подрешетки с противоположной спонтанной намагниченностью реализуются, но с различной интенсивностью намагничения. Поэтому имеется результирующая спонтанная намагниченность, хотя и более слабая, чем у ферромагнетиков. Вещества, проявляющие ферримагнетизм, называются ферримагнетиками или ферритами. Как и ферромагнетики, ферриты обладают остаточной намагниченностью, коэрцетивной силой. По сравнению с ферромагнетиками, ферриты имеют очень малую электропроводность – их преимущество для применения в радиотехнике.

Ферромагнитный резонансобусловлен взаимодействием спиновых магнитных моментов электронов с переменным электромагнитным полем. Это взаимодействие носит коллективный характер в пределах каждого домена. Поэтому явление резонанса в ферромагнетике проявляется на фоне согласованной прецессии спиновых магнитных моментов электронов во внешнем магнитном поле. Прецессия согласована обменным взаимодействием спинов. То есть, внутреннее магнитное поле, обусловленное спиновым взаимодействием, участвует, наряду с внешним магнитным полем, в формировании прецессии спиновой системы. Ферромагнитный резонанс наблюдается в диапазоне СВЧ – на частотах в тысячи МГц. Резонанс спиновой системы проявляется в резком изменении интенсивности переменного поля на определенной частоте, зависящей от рода материала. За счет неоднородности материала и его доменной структуры появляются дополнительные пики резонансных сигналов на других частотах. Как и парамагнитный резонанс, ферромагнитный резонанс имеет квантовую природу. Изучение спектров сигналов резонанса позволяет измерить ряд характеристик ферромагнетика: намагниченность насыщения, гиромагнитное отношение, константу анизотропии и др.

Анизотропия намагничивания. Ферромагнитные свойства монокристаллов зависят от направления намагничивания. Кривые намагничивания получаются различными в зависимости от ориентации намагничивающего поля относительно осей кристаллической решетки. Ось легкого (трудного) намагничивания определяет направление, в котором намагниченность при заданной величине поля максимальна (минимальна).

Не нашли то, что искали? Воспользуйтесь поиском:

Всем доброго времени суток. В прошлой статье я рассказывал о основной характеристике магнитного поля – магнитной индукции, однако приведённые расчётные формулы соответствуют магнитному полю в вакууме. Что в практической деятельности встречается довольно редко. Когда проводники с током находятся в какой–либо среде, даже в воздухе, магнитное поле, которое они создают, претерпевает некоторые, а иногда и существенные изменения. Какие изменения происходят с магнитным полем, и от чего это зависит, я расскажу в данной статье.

Как связана индукция и напряженность магнитного поля?

Магнетиком называется вещество, которое под действием магнитного поля способно намагничиваться (или как говорят физики приобретать магнитный момент). Магнетиками являются практически все вещества. Намагничивание веществ объясняется тем, что в веществах присутствуют свои собственные микроскопические магнитные поля, которые создаются вращением электронов по своим орбитам. Когда внешнее магнитное поле отсутствует, то микроскопические поля расположены произвольным образом, а под воздействием внешнего магнитного поля соответствующим образом ориентируются.

Для характеристики намагничивания различных веществ используют так называемый вектор намагничивания J.

Таким образом, под действием внешнего магнитного поля с магнитной индукцией В₀, магнетик намагничивается и создает свое магнитное поле с магнитной индукцией В’. В итоге общая индукция В будет состоять из двух слагаемых

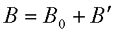
Тут возникает проблема вычисления магнитной индукции намагниченного вещества В’, для решения которой необходимо считать электронные микротоки всего вещества, что практически нереально.

Альтернативой данного решения есть ввод вспомогательных параметров, а именно напряженность магнитного поля Н и магнитная восприимчивость χ. Напряженность связывает магнитную индукцию В и намагничивание вещества J следующим выражением

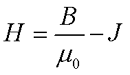
где В – магнитная индукция,

μ₀ – магнитная постоянная, μ₀ = 4π*10 -7 Гн/м.

В то же время вектор намагничивания J связан с напряженность магнитного поля В параметром, характеризующим магнитные свойства вещества и называемым магнитной восприимчивостью χ

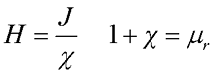
где J – вектор намагничивания вещества,

μ_r – относительная магнитная проницаемость вещества.

Однако наиболее часто для характеристики магнитных свойств веществ используют относительную магнитную проницаемость μ_r.

Таким образом, связь между напряженностью и магнитной индукцией будет иметь следующий вид

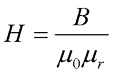
где μ₀ – магнитная постоянная, μ₀ = 4π*10 -7 Гн/м,

μ_r – относительная магнитная проницаемость вещества.

Так как намагничивание вакуума равна нулю (J = 0), то напряженность магнитного поля в вакууме будет равна

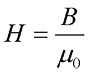
Отсюда можно вывести выражения напряженности для магнитного поля, создаваемого прямым проводом с током:

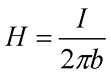
где I – ток протекающий по проводнику,

b – расстояние от центра провода до точки, в которой считается напряженность магнитного поля.

Как видно из данного выражения единицей измерения напряженности является ампер на метр (А/м) или эрстед (Э)

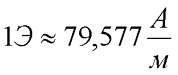
Таким образом, магнитная индукция В и напряженность Н являются основными характеристиками магнитного поля, а магнитная проницаемость μ_r – магнитной характеристикой вещества.

Намагничивание ферромагнетиков

В зависимости от магнитных свойств, то есть способности намагничиваться под действием внешнего магнитного поля, все вещества делятся на несколько классов. Которые характеризуются разной величиной относительной магнитной проницаемости μ_r и магнитной восприимчивости χ. Большинство веществ являются диамагнетиками (χ = -10 -8 … -10 -7 и μ_r -7 … 10 -6 и μ_r > 1), несколько реже встречаются ферромагнетики (χ = 10 3 … 10 5 и μ_r >> 1). Кроме данных классов магнетиков существует ещё несколько классов магнетиков: антиферромагнетики, ферримагнетики и другие, однако их свойства проявляются только при определённых условиях.

Особый интерес в радиоэлектронике ферромагнитные вещества. Основным отличием данного класса веществ является нелинейная зависимость намагничивания, в отличие от пара- и диамагнетиков, имеющих линейную зависимость намагничивания J от напряженности Н магнитного поля.

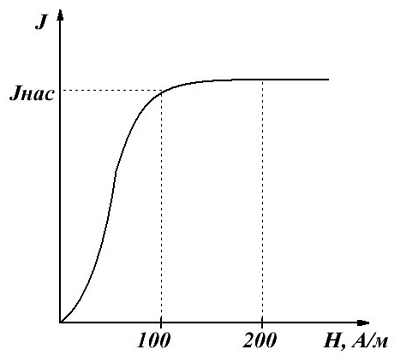
Зависимость намагничивания J ферромагнетика от напряженности Н магнитного поля.

На данном графике показана основная кривая намагничивания ферромагнетика. Изначально намагниченность J, в отсутствие магнитного поля (Н = 0), равна нулю. По мере возрастания напряженности намагничивание ферромагнетика проходит довольно интенсивно, вследствие того что его магнитная восприимчивость и проницаемость очень велика. Однако по достижении напряженности магнитного поля порядка H ≈ 100 А/м увеличение намагниченности прекращается, так как достигается точка насыщения J_НАС. Данное явление называется магнитным насыщением. В данном режиме магнитная проницаемость ферромагнетиков сильно падает и при дальнейшем увеличении напряженности магнитного поля стремится к единице.

Гистерезис ферромагнетиков

Еще одной особенностью ферромагнетиков является наличие петли гистерезиса, которая является основополагающим свойством ферромагнетиков.

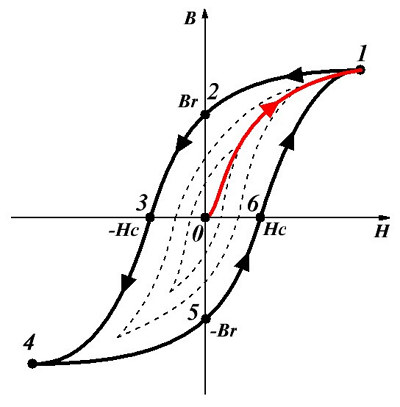
Петля гистерезиса ферромагнетика.

Для понимания процесса намагничивания ферромагнетика изобразим зависимость индукции В от напряженности Н магнитного поля, где красным цветом выделим основную кривую намагничивания. Данная зависимость довольно неопределенна, так как зависит от предыдущего намагничивания ферромагнетика.

Возьмём образец ферромагнитного вещества, которое не подвергалось намагничиванию (точка 0) и поместим его в магнитное поле, напряженность Н которого начнем увеличивать, то есть зависимость будет соответствовать кривой 0 – 1, пока не будет достигнуто магнитное насыщение (точка 1). Дальнейшее увеличение напряженности не имеет смысла, потому как намагниченность J практически не увеличивается, а магнитная индукция увеличивается пропорционально напряженности Н. Если же начинать уменьшать напряженность, то зависимость В(Н) будет соответствовать кривой 1 – 2 – 3, при этом когда напряженность магнитного поля упадёт до нуля (точка 2), то магнитная индукция не упадёт до нуля, а будет равна некоторому значению B_r, которое называется остаточной индукцией, а намагничивание будет иметь значение J_r, называемое остаточным намагничиванием.

Для того чтобы снять остаточное намагничивание и уменьшить остаточную индукцию B_r до нуля, необходимо создать магнитное поле, противоположное полю, вызвавшему намагничивание, причем напряженность размагничивающего поля должна составлять Н_с, называемая коэрцитивной силой. При дальнейшем росте напряженности магнитного поля, которое противоположно первоначальному полю, происходит насыщение ферромагнетика (точка 4).

Таким образом, при действии на ферромагнетик переменного магнитного поля зависимость индукции от напряженности будет соответствовать кривой 1 – 2 – 3 – 4 – 5 – 6 – 1, которая называется петлёй гистерезиса. Таких петель для ферромагнетика может быть множество (пунктирные кривые), называемые частными циклами. Однако, если при максимальных значениях напряженности магнитного поля происходит насыщение, то получается максимальная петля гистерезиса (сплошная кривая).

Так как магнитная проницаемость μ_r ферромагнетиков имеет довольно сложную зависимость от напряженности магнитного поля, поэтому нормируются два параметра магнитной проницаемости:

μ_н – начальная магнитная проницаемость соответствует напряженности Н = 0;

μ_max – максимальная магнитная проницаемость достигается в магнитном поле при приближении магнитного насыщения.

Таким образом, у ферромагнетиков величины B_r, Н_с и μ_н (μ_max) являются основными характеристиками, влияющими на выбор вещества в конкретном случае.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.