Зависимость сопротивления металлических проводников от температуры

Зависимость сопротивления проводника от температуры

Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что

1. возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
2. изменяется их концентрация при нагревании проводника.

Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:

ho_t =
ho_0 (1 + alpha t) ,) (

R_t = R_0 (1 + alpha t) ,)

где ρ₀, ρ_t — удельные сопротивления вещества проводника соответственно при 0 °С и t °C; R₀, R_t — сопротивления проводника при 0 °С и t °С, α — температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1 ). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.

Температурный коэффициент сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.

mathcal h alpha mathcal i) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ.

Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. У чистых металлов α = 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов) n = const и увеличение ρ происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.

Для растворов электролитов α -1 . Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.

Формулы зависимости ρ и R от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором α = const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.

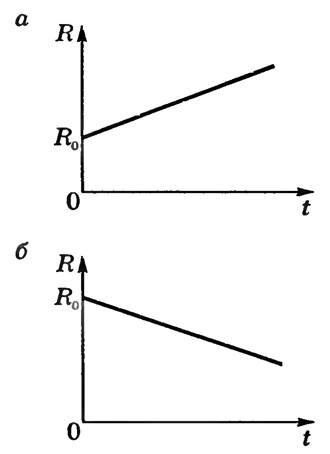
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.

При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости. Металл переходит в сверхпроводящее состояние.

Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.

Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 256-257.

«Физика – 10 класс»

Какую физическую величину называют сопротивлением
От чего и как зависит сопротивление металлического проводника?

Различные вещества имеют разные удельные сопротивления. Зависит ли сопротивление от состояния проводника? от его температуры? Ответ должен дать опыт.

Если пропустить ток от аккумулятора через стальную спираль, а затем начать нагревать её в пламени горелки, то амперметр покажет уменьшение силы тока. Это означает, что с изменением температуры сопротивление проводника меняется.

Если при температуре, равной 0 °С, сопротивление проводника равно R₀, а при температуре t оно равно R, то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры t:

Коэффициент пропорциональности α называют температурным коэффициентом сопротивления.

Температурный коэффициент сопротивления — величина, равная отношению относительного изменения сопротивления проводника к изменению его температуры.

Он характеризует зависимость сопротивления вещества от температуры.

Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании на 1 К (на 1 °С).

Для всех металлических проводников коэффициент α > 0 и незначительно меняется с изменением температуры. Если интервал изменения температуры невелик, то температурный коэффициент можно считать постоянным и равным его среднему значению на этом интервале температур. У чистых металлов

У растворов электролитов сопротивление с ростом температуры не увеличивается, а уменьшается. Для них α -1 .

При нагревании проводника его геометрические размеры меняются незначительно. Сопротивление проводника меняется в основном за счёт изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры, если в формулу (16.1) подставить значения Вычисления приводят к следующему результату:

где ΔТ — изменение абсолютной температуры.

Так как а мало меняется при изменении температуры проводника, то можно считать, что удельное сопротивление проводника линейно зависит от температуры (рис. 16.2).

Увеличение сопротивления можно объяснить тем, что при повышении температуры увеличивается амплитуда колебаний ионов в узлах кристаллической решётки, поэтому свободные электроны сталкиваются с ними чаще, теряя при этом направленность движения. Хотя коэффициент а довольно мал, учёт зависимости сопротивления от температуры при расчёте параметров нагревательных приборов совершенно необходим. Так, сопротивление вольфрамовой нити лампы накаливания увеличивается при прохождении по ней тока за счёт нагревания более чем в 10 раз.

У некоторых сплавов, например у сплава меди с никелем (Константин), температурный коэффициент сопротивления очень мал: α ≈ 10 -5 К -1 ; удельное сопротивление Константина велико: ρ ≈ 10 -6 Ом • м. Такие сплавы используют для изготовления эталонных резисторов и добавочных резисторов к измерительным приборам, т. е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.

Существуют и такие металлы, например никель, олово, платина и др., температурный коэффициент которых существенно больше: α ≈ 10 -3 К -1 . Зависимость их сопротивления от температуры можно использовать для измерения самой температуры, что и осуществляется в термометрах сопротивления.

На зависимости сопротивления от температуры основаны и приборы, изготовленные из полупроводниковых материалов, — термисторы. Для них характерны большой температурный коэффициент сопротивления (в десятки раз превышающий этот коэффициент у металлов), стабильность характеристик во времени. Номинальное сопротивление термисторов значительно выше, чем у металлических термометров сопротивления, оно обычно составляет 1, 2, 5, 10, 15 и 30 кОм.

Обычно в качестве основного рабочего элемента термометра сопротивления берут платиновую проволоку, зависимость сопротивления которой от температуры хорошо известна. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить.Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.

Сверхпроводимость.

Сопротивление металлов уменьшается с уменьшением температуры. Что произойдёт при стремлении температуры к абсолютному нулю?

В 1911 г. голландский физик X. Камерлинг-Оннес открыл замечательное явление — сверхпроводимость. Он обнаружил, что при охлаждении ртути в жидком гелии её сопротивление сначала меняется постепенно, а затем при температуре 4,1 К очень резко падает до нуля (рис. 16.3).

Явление падения до нуля сопротивления проводника при критической температуре называется сверхпроводимостью.

Открытие Камерлинг-Оннеса, за которое в 1913 г. ему была присуждена Нобелевская премия, повлекло за собой исследования свойств веществ при низких температурах. Позже было открыто много других сверхпроводников.

Сверхпроводимость многих металлов и сплавов наблюдается при очень низких температурах — начиная примерно с 25 К. В справочных таблицах приводятся температуры перехода в сверхпроводящее состояние некоторых веществ.

Температура, при которой вещество переходит в сверхпроводящее состояние, называется критической температурой.

Критическая температура зависит не только от химического состава вещества, но и от структуры самого кристалла. Например, серое олово имеет структуру алмаза с кубической кристаллической решёткой и является полупроводником, а белое олово обладает тетрагональной элементарной ячейкой и является серебристо-белым, мягким, пластичным металлом, способным при температуре, равной 3,72 К, переходить в сверхпроводящее состояние.

У веществ в сверхпроводящем состоянии были отмечены резкие аномалии магнитных, тепловых и ряда других свойств, так что правильнее говорить не о сверхпроводящем состоянии, а об особом, наблюдаемом при низких температурах состоянии вещества.

Если в кольцевом проводнике, находящемся в сверхпроводящем состоянии, создать ток, а затем удалить источник тока, то сила этого тока не меняется сколь угодно долго. В обычном же (несверхпроводящем) проводнике электрический ток в этом случае прекращается.

Сверхпроводники находят широкое применение. Так, сооружают мощные электромагниты со сверхпроводящей обмоткой, которые создают магнитное поле на протяжении длительных интервалов времени без затрат энергии. Ведь выделения тепла в сверхпроводящей обмотке не происходит.

Однако получить сколь угодно сильное магнитное поле с помощью сверхпроводящего магнита нельзя. Очень сильное магнитное поле разрушает сверхпроводящее состояние. Такое поле может быть создано и током в самом сверхпроводнике. Поэтому для каждого проводника в сверхпроводящем состоянии существует критическое значение силы тока, превысить которое, не нарушая сверхпроводящего состояния, нельзя.

Сверхпроводящие магниты используются в ускорителях элементарных частиц, магнитогидродинамических генераторах, преобразующих механическую энергию струи раскалённого ионизованного газа, движущегося в магнитном поле, в электрическую энергию.

Объяснение сверхпроводимости возможно только на основе квантовой теории. Оно было дано лишь в 1957 г. американскими учёными Дж. Бардиным, Л. Купером, Дж. Шриффером и советским учёным, академиком Н. Н. Боголюбовым.

В 1986 г. была открыта высокотемпературная сверхпроводимость. Получены сложные оксидные соединения лантана, бария и других элементов (керамики) с температурой перехода в сверхпроводящее состояние около 100 К. Это выше температуры кипения жидкого азота при атмосферном давлении (77 К).

Высокотемпературная сверхпроводимость в недалёком будущем приведёт наверняка к новой технической революции во всей электротехнике, радиотехнике, конструировании ЭВМ. Сейчас прогресс в этой области тормозится необходимостью охлаждения проводников до температур кипения дорогого газа — гелия.

Физический механизм сверхпроводимости довольно сложен. Очень упрощённо его можно объяснить так: электроны объединяются в правильную шеренгу и движутся, не сталкиваясь с кристаллической решёткой, состоящей из ионов. Это движение существенно отличается от обычного теплового движения, при котором свободный электрон движется хаотично.

Надо надеяться, что удастся создать сверхпроводники и при комнатной температуре. Генераторы и электродвигатели станут исключительно компактными (уменьшатся в несколько раз) и экономичными. Электроэнергию можно будет передавать на любые расстояния без потерь и аккумулировать в простых устройствах.

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Электрический ток в различных средах – Физика, учебник для 10 класса – Класс!ная физика

Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что

1. возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
2. изменяется их концентрация при нагревании проводника.

Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:

ho_t =
ho_0 (1 + alpha t) ,) (

R_t = R_0 (1 + alpha t) ,)

где ρ 0 , ρ t – удельные сопротивления вещества проводника соответственно при 0 °С и t °C; R 0 , R t – сопротивления проводника при 0 °С и t °С, α – температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.

Температурный коэффициент сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.

mathcal h alpha mathcal i) – среднее значение температурного коэффициента сопротивления в интервале ΔΤ .

Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. У чистых металлов α = 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов) n = const и увеличение ρ происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.