Проведите доказательство рассмотренных в параграфе логических законов с помощью таблиц истинности.
Ответ
Распределительный закон для логического сложения: A v (B & C) = (A v B) & (A v C).
Равенство значений столбца A v (B & C) и столбца (A v B) & (A v C) доказывает распределительный закон.
преобразования логических выражений
Логические выражения называются равносильными, если их истинностные значения совпадают при любых значениях, входящих в них логических переменных. В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. Приведем соотношения, отражающие эти законы.
1. Закон двойного отрицания:
А =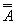 
. Двойное отрицание исключает отрицание.
2. Переместительный (коммутативный) закон:
для логического сложения: А к B = B к A ;
для логического умножения: A & B = B & A .
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
В обычной алгебре a + b = b + a, a Д b = b Д a.
3. Сочетательный (ассоциативный) закон:
для логического сложения: ( A к B ) к C = A к ( B к C );
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
В обычной алгебре: (a + b) + c = a + (b + c) = a + b + c,
а Д ( b Д c ) = a Д ( b Д c ) = a Д b Д c .
4. Распределительный (дистрибутивный) закон:
для логического сложения: ( A к B )& C = ( A & C ) к ( B & C );
для логического умножения: ( A & B ) к C = ( A к C )&( B к C ).
Определяет правило выноса общего высказывания за скобку.
В обычной алгебре: (a + b) Д c = a Д c + b Д c.
5. Закон общей инверсии (законы де Моргана):
для логического сложения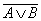 
= 
& 
;
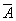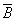для логического умножения: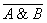 
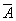= к
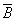
6. Закон идемпотентности ( от латинских слов idem тот же самый и potens сильный; дословно равносильный):
для логического сложения: A к A = A ;
для логического умножения: A & A = A .
Закон означает отсутствие показателей степени.
7. Законы исключения констант:
для логического сложения: A к 1 = 1, A к 0 = A ;
для логического умножения: A &1 = A , A &0 = 0.
8. Закон противоречия: A& 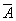= 0.
Невозможно, чтобы противоречащие высказывания были одновременно истинными.
9. Закон исключения третьего: A к 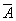= 1.
Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе ложно, третьего не дано.
для логического умножения: A &( A к B ) = A .
11. Закон исключения (склеивания):
для логического сложения: ( A & B ) к ( 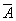& B ) = B ;
для логического умножения: ( A к B )&( 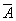к B ) = B .
12. Закон контрапозиции (правило перевертывания): ( A л B ) = ( B л A ).
Справедливость приведенных законов можно доказать табличным способом: выписать все наборы значений А и В, вычислить на них значения левой и правой частей доказываемого выражения и убедиться, что результирующие столбцы совпадут.
Пример. Найдите X, если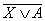 
к 
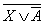= В.
Для преобразования левой части равенства последовательно воспользуемся законом де Моргана для логического сложения и законом двойного отрицания:
( 
& 
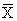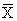) к ( & A )
Согласно распределительному закону для логического сложения:
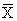&( к A )
Согласно закону исключения третьего и закона исключения констант:
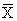&1 =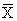
Полученную левую часть приравняем правой:
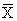= В
Окончательно получим, что X =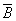 
.
Пример 2. Упростите логическое выражение ( A к B к C )&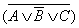 
Правильность упрощения проверьте с помощью таблиц истинности для исходного и полученного логического выражения.
Согласно закону общей инверсии для логического сложения (первому закону Моргана) и закону двойного отрицания:
( A к B к C )&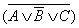 
= ( A к B к C )&( & B & 
)
Согласно распределительному (дистрибутивному) закону для логического сложения:
(A к B к C )&( &B& ) = (A& ) к (B& ) к (C& ) к (A&B) к (B&B) к (C&B) к (A& ) к (B& ) к (C& )
Согласно закона противоречия: ( A & ) = 0; ( C & ) = 0
Согласно закона идемпотентности ( B & B ) = B
Подставляем значения и, используя переместительный (коммутативный) закон и группируя слагаемые, получаем:
0 к ( A & B ) к ( & B ) к B к ( C & B ) к ( & B ) к ( C & ) к ( A & ) к 0
Согласно закона исключения (склеивания)
( A & B ) к ( & B ) = B
( C & B ) к ( & B ) = B
Подставляем значения и получаем:
0 к B к B к B к ( C & ) к ( A & ) к 0
Согласно закона исключения констант для логического сложения и закона идемпотентности:
Подставляем значения и получаем:
B к ( C & ) к ( A & )
Согласно распределительному (дистрибутивному) закону для логического умножения:
( C & ) к ( A & ) = ( C к A )&( C к )&( к A )&( к )
Согласно закона исключения третьего: ( C к ) = 1 ( к A ) = 1
Подставляем значения и окончательно получаем: B & & .
Урок " Логические законы "
Логические законы и правила преобразования
Если логическое выражение содержит большое количество операций, то составлять для него таблицу истинности достаточно сложно, так как приходится перебирать большое количество вариантов. В таких случаях формулы удобно привести в нормальную форму.
Формула имеет нормальную форму, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания, при этом знаки отрицания находятся только при логических переменных.
Для приведения формулы к нормальной форме используют законы логики и правила логических преобразований.
Законы логики отражают наиболее важные закономерности логического мышления. В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений.
Закон тождества
Всякое высказывание тождественно самому себе.
Закон непротиворечия
Высказывание не может быть одновременно истинным и ложным. Если высказывание А истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно.
Закон исключенного третьего
Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение «истина».
Закон двойного отрицания
Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание.
Законы де Моргана
Важное значение для выполнения преобразований логических выражений имеют законы алгебраических преобразований. Многие из них имеют аналоги в алгебре.
(переместительный)
В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения.
(сочетательный)
Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять.
(А & B ) & С = А & (В & С)
(А / В) / С= А / (В / С)
(распределительный )
В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые.
Закон поглощения
Ø A & (A / B) = Ø A & B
A / Ø A & B = A / B
Рассмотрим в качестве примера применения законов логики преобразование логического выражения. Пусть нам необходимо упростить логическое выражение:
Воспользуемся законом дистрибутивности и вынесем за скобки А:
(А & В) v (А & ¬ В) = А & (В v ¬ В).
По закону исключенного третьего В v В =1, следовательно: