Содержание
Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С1 – ёмкость первого;
С2 – ёмкость второго;
С3 – ёмкость третьего;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается 
.
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.
Параллельное соединение электролитов
Схема параллельного соединения
В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.
Последовательное соединение электролитов
Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены :)
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
П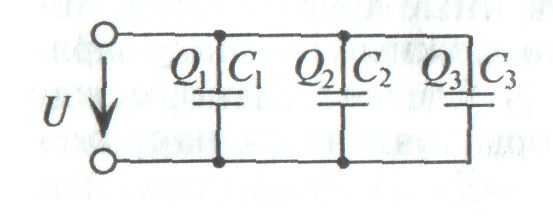
ри параллельном соединении конденсаторов к каждому конденсатору приложено одинаковое напряжениеU, а величина заряда на обкладках каждого конденсатора Q пропорциональна его емкости (рис. 2).
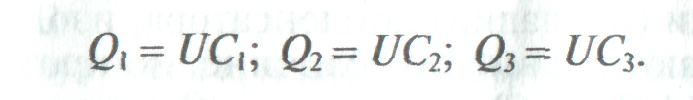
Общий заряд Q всех конденсаторов
Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.
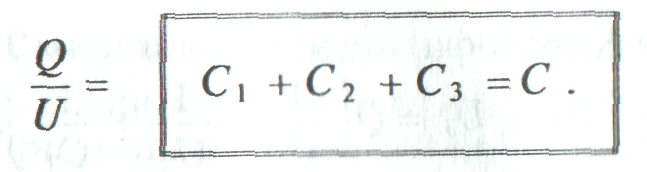
Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов применяется для увеличения емкости.
4)Если параллельно включены т одинаковых конденсаторов емкостью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением
Последовательное соединение конденсаторов
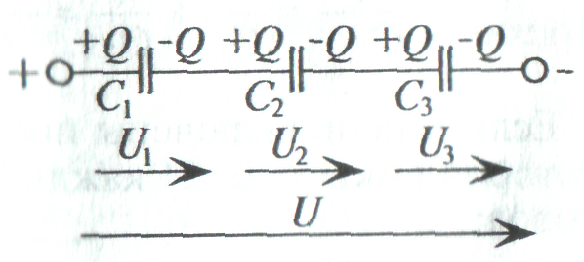
На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U, появятся заряды одинаковые по величине с противоположными знаками.
Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:
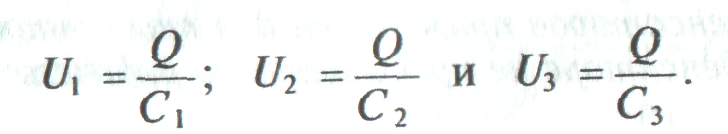
Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих конденсаторов.
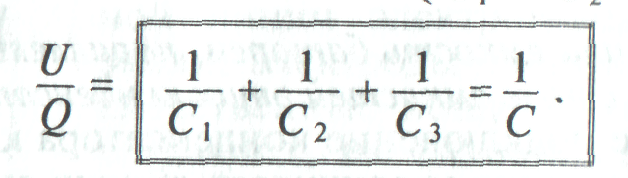
При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:
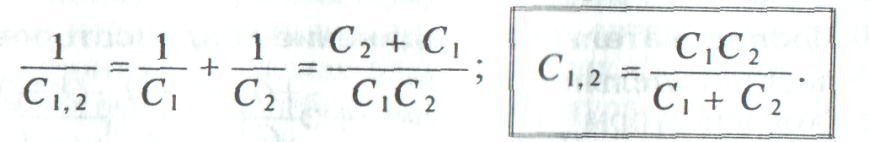
Если в цепь включены последовательно п одинаковых конденсаторов емкостью С каждый, то общая емкость этих конденсаторов:
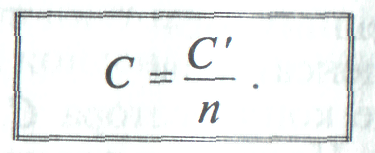
Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. последовательное включение конденсаторов приводит к уменьшению общей емкости батареи конденсаторов.
На практике может оказаться , что допустимое рабочее напряжение Up конденсатора меньше напряжения, на которое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить несколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется меньше его допустимого рабочего Up. Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения Up.
Смешанное соединение конденсаторов
Смешанное соединение (последовательно-параллельное) конденсаторов применяют тогда, когда необходимо увеличить емкость и рабочее напряжение батареи конденсаторов.
Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.
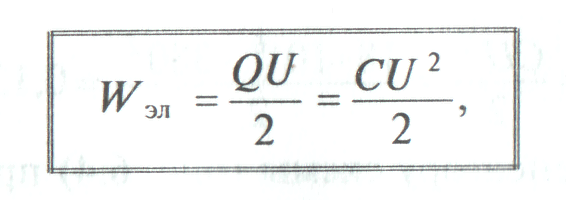
где Q — заряд конденсатора или конденсаторов, к которым приложено напряжение U; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U.
Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.
15.Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)
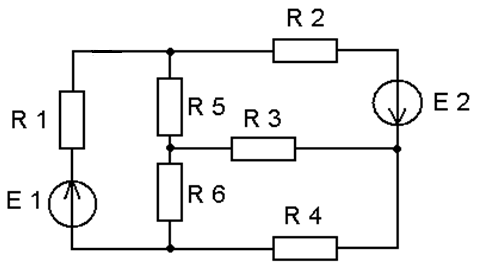
Рисунок 5- Схема электрическая
Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.
На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.
1.Схемы замещения элементов электрических цепей
На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).
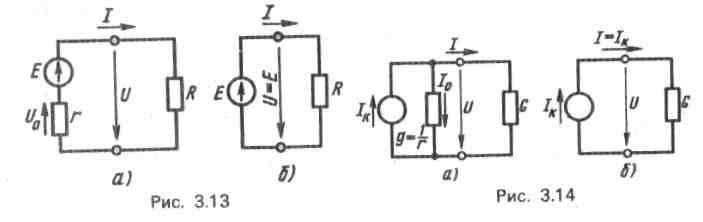
Приr= 0 внутреннее падение напряженияUо = 0, поэтому
напряжение на зажимах источника при любом токе равно
В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияIK, а вместо внутреннего сопротивления в расчет вводится внутренняя проводимостьg=1/r.
Возможность такой замены можно доказать, разделив равенство (3.1) на r:
где U/r = Io—некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E/r = IK — ток короткого замыкания источника;
Вводя новые обозначения, получим равенство IK = Io + I, которому удовлетворяет эквивалентная схема рис. 3.14,а.
В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):
Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.
Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
Сократив выражение на Q, получим знакомую формулу:
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
Так как заряд конденсатора
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
Пример 1
Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С1 = 10 мкФ, C2 = 2 мкФ, C3 = 5 мкФ, а C4 = 1 мкФ?
При последовательном соединении общая емкость равна:
При параллельном соединении общая емкость равна:
Пример 2
Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С1 = 7 мкФ, С2 = 2 мкФ, С3 = 1 мкФ.
Сначала найдем общую емкость параллельного участка цепи:
Затем найдем общую емкость для всей цепи:
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
