Содержание
Емкость конденсаторов, проводов и других элементов электрической цепи измеряется в фарадах (Ф); индуктивность проводов, катушек и других элементов цепей измеряется в генри (Гн).
Емкость плоского конденсатора, состоящего из п пластин площадью пластины 

где d — расстояние между пластинами, м.
Емкость цилиндрического конденсатора (коаксиального кабеля) длиной / (м), Ф:

где R1 — радиус внутренней обкладки (жилы), м;
R2 — радиус внешней обкладки, м.
Емкость прямолинейного провода длиной / и радиусом поперечного сечения г (м) (второй провод — в бесконечности), Ф:

Индуктивность уединенного прямолинейного провода круглого сечения радиусом г и длиной / (м), Гн:

Индуктивность кольца со средним радиусом R и радиусом сечения кольца г0 (м), Гн:

Индуктивность многослойной катушки толщиной обмотки d, радиусом обмотки R (от оси до среднего слоя обмотки), длиной / (м) и числом витков w (рис. 1.2, а), Гн


Индуктивность тороидальной катушки кругового сечения (рис. 1.2, б), Гн:

где w — число витков катушки,
D — средний диаметр тора, м;
d — диаметр среднего витка, м.
Взаимная индуктивность двух тороидальных катушек с числами витков w^ и w2, Гн:


Рис. 1.3. Концентрически расположенные катушки индуктивности
Взаимная индуктивность концентрических катушек прямоугольного сечения, имеющих одинаковую длину и примыкающих друг к другу (рис. 1.3), Гн:

где L12 — индуктивность катушки, состоящей из первой и второй катушек;
L1, L2 — собственные индуктивности катушек.
После несложной процедуры регистрации Вы сможете пользоваться всеми сервисами и создать свой веб-сайт.
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
– Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
– Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Свободные электрические колебания в параллельном контуре.
Основные свойства индуктивности:
– Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией  .
.
– Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит .
.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.

Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t1, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 =  .
.
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит .
.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1, он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.
В течении заключительного этапа колебания (t4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний  .
.
Частота свободных колебаний контура ƒ = 1 / T
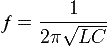
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности XL=2πfL равно реактивному сопротивлению ёмкости XC=1/(2πfC).
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчёт ёмкости:
Расчёт индуктивности:
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!

По формуле циклической частоты свободных электромагнитных колебаний , где L – индуктивность катушки (Гн), C – ёмкость конденсатора (Ф). Циклическую частоту расписываем как: , где V – "ню" частота колебаний (Гц). Данную формулу подставляем в формулу циклической частоты свободных электромагнитных колебаний: . Поизводим преобразования и выражаем искомую ёмкость конденсатора:
В системе СИ: 10 МГц = 10*10⁶ Гц; 5,1 мкГн = 5,1*10⁻⁶ Гн. Подставляеи вычисляем:
