Содержание
Читайте также:
- E. ПОРЯДОК ДЕЙСТВИЯ ОСНОВНЫХ ПРАВ И СВОБОД 51
- I. Анализ результатов контрольной работы.
- I. Анализ результатов самостоятельной работы.
- I. Организация учащихся на выполнение работы.
- I. Организация учащихся на выполнение работы.
- I. Организация учащихся на выполнение работы.
- I. Организация учащихся на выполнение работы.
- I. Организация учащихся на выполнение работы.
- I. Организация учащихся на выполнение работы.
- I. Организация учащихся на выполнение работы.
- I. Организация учащихся на выполнение работы.
- I. Организация учащихся на выполнение работы.
Упражнение № 1. Определение индуктивности катушки и зависимости ее индуктивного сопротивления от частоты переменного тока
1. Собрать схему установки, изображенной на рисунке 10, подключив к клеммам "L, C, ткань" катушку индуктивности.
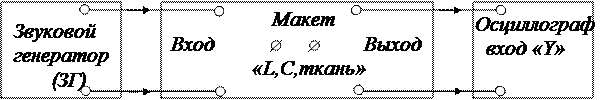 |
Рисунок 10.
Структурная схема экспериментальной установки
2. Приступая к выполнению работы, установите следующие положения переключателей на осциллографе: кнопка "вход х"- в нажатом положении; ручки "стабильность" и "уровень"- в крайнее правое положение; ручку "вольт/делен." – на 0,1 В/дел.
На звуковом генераторе (ЗГ): ручками "множитель" и "лимб частоты" (в виде диска) установить частоту 300 Гц (на лимбе частоты должно быть 3, а множитель в положении "100"); ручку "амплитуда" (регулировка выходного напряжения) – в среднее положение. Переключатель «форма» на звуковом генераторе установить в положение «
». Другие переключатели и кнопки на приборах устанавливаются преподавателем или лаборантом.
3. На макете ручку "потенциометр" поставить в крайнее левое положение – (минимум).
4. Включить осциллограф и генератор (тумблер «сеть» расположен на обратной стороне прибора) в сеть. Через 1-2 минуты приступить к измерениям. На осциллографе ручками «Ò» и “☼”, “↔” и ”↕” установить не очень яркую четкую светящуюся точку в центре экрана.
5. Плавным вращением ручки "потенциометр" на макете и "амлитуда" на ЗГ установить по микроамперметру на макете ток силой в 200 мкА.
6. Измерить значение напряжения на катушке с помощью осциллографа. Для этого ручкой "вольт/делен" подобрать такую цену деления, чтобы вертикальная светящаяся линия составляла от 3-х до 6 больших делений. Эффективное напряжение Uэф рассчитывается по формуле:
где: dy – число делений по оси "Y" на осциллографе с точностью до 0,2 дел.
Cy – цена одного большого деления, задается ручкой "вольт/делен." измеренные значения dy и Cy и вычисленные значения Uэф занесите в таблицу 1.
7. Повторить измерения при всех частотах (множитель частоты «1к» соответствует умножению на 1000, 10к – 10000), указанных в таблице 1, поддерживая с помощью ручки "потенциометр" на макете и "амплитуда " на ЗГ силу тока, равную 200 мкА. (если на высоких частотах не удается установить ток 200 мкА, то взять значение тока 100 мкА).
Результаты измерений занесите в таблицу 1.
| n, Гц | dy, дел. | Cy, В/дел. | Uэф, В | Iэф, мкА | R, Ом | Z, Ом | XL, Ом | L, Гн |
8. Отсоединить катушку индуктивности от макета.
9. Рассчитать значения Z, XL, L по формулам:
Z = Uэф/Iэф. 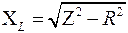 .
. 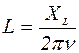
Т.к. R (указано на катушке) мало в сравнении с Z, то будем считать XL » Z.
10. Построить график зависимости XL= f(n). По оси Х – частота n, по оси Y – ХL.
Упражнение №2. Определение емкости конденсатора и зависимости его емкостного сопротивления от частоты переменного тока
1. К клеммам "L,C, ткань" макета подсоединить конденсатор С.
2. Измерить и рассчитать значения dy, Cy, Uэф, Iэф, ХС, С и занести их в таблицу 2, устанавливая частоты, указанные в таблице 2. Методика измерений остается такой же, что и в упражнении 1.
3. Выключить приборы из сети и отключить конденсатор С.
ХC=Uэф/Iэф; 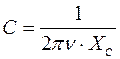
рассчитать емкостное сопротивление ХC и емкость конденсатора С.
| n, Гц | Dy, дел. | Cy,В/дел | Uэф, В | Iэф, мкА | Хс, Ом | С, Ф |
5. Построить график зависимости ХC= f (n). По оси Х – частоту ν, по оси Y – Хc.
Упражнение 3. Определение зависимости импеданса биологического объекта от частоты переменного тока и его активного сопротивления RT
1. Поместить игольчатые электроды в объект (картофели0на) на расстоянии не менее 4 см и подсоединить их к клеммам "L,C, ТКАНЬ" макета.
2. Включить ЗГ и осциллограф в сеть.
3. Для частот, указанных в таблице 3 произвести измерения dy, Cy, Uэф, Iэф, Z и результаты занести в таблицу 3.
4. Отключить приборы от сети.
5. По формуле: Z=Uэф/Iэф, вычислить импеданс и построить график его зависимости от частоты переменного тока Z= f (n). По оси Х – n, по оси Y – Z .0
6. Для n = 20000 Гц по графику оценить RТ (см. рис.11) и по формуле: сos j = RТ/Z, рассчитать сos j для исследуемых частот.
7. Из формулы 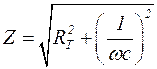 при какой-то частоте найти величину электроемкости ткани между электродами в данных условиях при какой-то частоте, например при
при какой-то частоте найти величину электроемкости ткани между электродами в данных условиях при какой-то частоте, например при 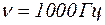 . Значение Z взять из таблицы 3 при выбранной частоте 1000 Гц.
. Значение Z взять из таблицы 3 при выбранной частоте 1000 Гц.
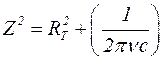 , откуда
, откуда 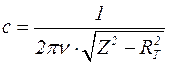 .
.
| n, Гц | dy, дел. | Cy, В/дел. | Uэф, В | Iэф, мкА | Z, Ом | RТ, Ом | 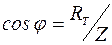 |
| RT≈Z При n = 20000 Гц |
8. Сравнить графики упражнений 2 и 3 и сделать вывод о природе импеданса биологического объекта.
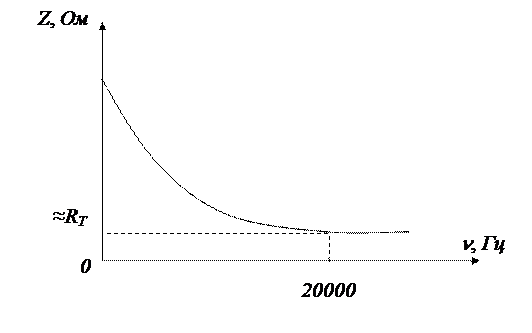 |
Рисунок 11.
Зависимость импеданса биологической ткани от частоты Z=f(ν)
(Импеданс ткани 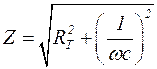 , где RT – активное сопротивление ткани (RT – const на всех частотах в данных условиях),
, где RT – активное сопротивление ткани (RT – const на всех частотах в данных условиях), 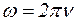 . При частоте
. При частоте 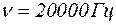
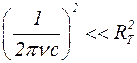 , поэтому
, поэтому 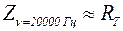 . Таким образом, за активное сопротивление биологической ткани RT в данном упражнении приблизительно принимаем значение импеданса Z при частоте
. Таким образом, за активное сопротивление биологической ткани RT в данном упражнении приблизительно принимаем значение импеданса Z при частоте 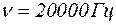 ).
).
Контрольные вопросы
1. Основные характеристики переменного тока (мгновенные, амплитудные, эффективные значения напряжения и силы переменного тока, период, частоту и фазу переменного тока).
2. Теории цепей переменного тока с R, L и C – нагрузками с выводом формул, векторные диаграммы.
3. Формулы импеданса при последовательном и параллельном соединении R, L и C с построением векторных диаграмм и выводом формул.
4. Закон Ома для цепи переменного тока.
5. Эквивалентные электрические схемы и емкостно-омическую природу импеданса биологической ткани.
6. Физические основы реографии.
Дата добавления: 2014-12-07 ; Просмотров: 337 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
В данной статье мы подробно поговорим про индуктивное сопротивление, реактивное сопротивление и треугольники напряжения, сопротивления и силы.
Введение
Итак, мы рассмотрели поведение индукторов, подключенных к источникам постоянного тока, и, надеюсь, теперь мы знаем, что когда на индуктор подается постоянное напряжение, рост тока через него происходит не мгновенно, а определяется индуктором, индуцированным самим индуктором или обратным значением ЭДС.
Также мы видели, что ток индукторов продолжает расти, пока не достигнет своего максимального установившегося состояния после пяти постоянных времени. Максимальный ток, текущий через индукционную катушку ограничиваются только резистивной частью катушек обмотки в омах, и как мы знаем из закона Ома, это определяется отношением напряжения к току V / R .
Когда переменное напряжение подается на катушку индуктивности, поток тока через него ведет себя совершенно иначе, чем при приложении постоянного напряжения. Эффект синусоидального питания приводит к разности фаз между напряжением и формами тока. Теперь в цепи переменного тока противодействие току, протекающему через обмотки катушек, зависит не только от индуктивности катушки, но и от частоты сигнала переменного тока.
Сопротивление току, протекающему через катушку в цепи переменного тока, определяется сопротивлением переменного тока, более известным как полное сопротивление (Z) цепи. Но сопротивление всегда связано с цепями постоянного тока, поэтому, чтобы отличить сопротивление постоянного тока от сопротивления переменного тока, обычно используется термин «реактивное сопротивление» .
Как и сопротивление, значение реактивного сопротивления также измеряется в омах, но ему присваивается символ X (заглавная буква «X»), чтобы отличить его от чисто резистивного значения.
Поскольку интересующий нас компонент является индуктором, реактивное сопротивление индуктора поэтому называется «Индуктивное реактивное сопротивление». Другими словами, электрическое сопротивление индуктивности при использовании в цепи переменного тока называется индуктивным сопротивлением .
Индуктивное сопротивление, которому дается символ X L , является свойством в цепи переменного тока, которое противодействует изменению тока. В наших уроках о конденсаторах в цепях переменного тока мы видели, что в чисто емкостной цепи ток I C «опережает» напряжение на 90 o . В чисто индуктивной цепи переменного тока верно обратное: ток I L отстает от напряжения на 90 o или (π / 2 рад).
Схема индуктивности переменного тока
В приведенной выше чисто индуктивной цепи индуктор подключен непосредственно через напряжение питания переменного тока. Когда напряжение питания увеличивается и уменьшается с частотой, самоиндуцированная обратная ЭДС также увеличивается и уменьшается в катушке по отношению к этому изменению.
Мы знаем, что эта самоиндуцированная ЭДС прямо пропорциональна скорости изменения тока через катушку и имеет наибольшее значение при переходе напряжения питания от положительного полупериода к отрицательному полупериоду или наоборот в точках 0 о и 180 о вдоль синусоиды.
Следовательно, минимальная скорость изменения напряжения возникает, когда синусоида переменного тока пересекается при своем максимальном или минимальном пиковом уровне напряжения. В этих положениях в цикле максимальный или минимальный токи протекают через цепь индуктора, и это показано ниже.
Векторная диаграмма индуктора переменного тока
Эти формы напряжения и тока показывают, что для чисто индуктивной цепи ток отстает от напряжения на 90 o . Также можно сказать, что напряжение опережает ток на 90 o . В любом случае общее выражение заключается в том, что ток отстает, как показано на векторной диаграмме. Здесь вектор тока и вектор напряжения показаны смещенными на 90 o . Ток отстает от напряжения .
Мы можем также написать это заявление как, V L = 0 ö и I L = -90 о по отношению к напряжению, V L . Если форма волны напряжения классифицируется как синусоида, то ток I L можно классифицировать как отрицательный косинус, и мы можем определить значение тока в любой момент времени как:
Поскольку ток всегда отстает от напряжения на 90 o в чисто индуктивной цепи, мы можем найти фазу тока, зная фазу напряжения или наоборот. Так что если мы знаем значение V L , то I L должно отставать на 90 o . Аналогичным образом, если мы знаем значение I L, то V L, следовательно, должно опережать на 90 o . Затем это отношение напряжения к току в индуктивном контуре будет производить уравнение, определяющее индуктивное сопротивление Х L катушки.
Мы можем переписать уравнение для индуктивного сопротивления в более привычную форму, которая использует обычную частоту питания вместо угловой частоты в радианах ω и это будет выглядеть так:
Из приведенного выше уравнения для индуктивного реактивного сопротивления можно видеть, что, если увеличить частоту, либо индуктивность, общее значение индуктивного реактивного сопротивления также увеличится. Когда частота приближается к бесконечности, реактивное сопротивление индукторов также увеличивается до бесконечности, действуя как разомкнутая цепь.
Однако, когда частота приближается к нулю или постоянному току, реактивное сопротивление индукторов будет уменьшаться до нуля, действуя как короткое замыкание. Это означает, что индуктивное сопротивление «пропорционально» частоте.
Другими словами, индуктивное реактивное сопротивление увеличивается с частотой, в результате чего X L будет небольшим на низких частотах, а X L будет высоким на высоких частотах, что продемонстрировано на графике ниже.
Индуктивное сопротивление от частоты
Затем мы видим, что при постоянном токе индуктор имеет нулевое реактивное сопротивление (короткое замыкание), на высоких частотах индуктор имеет бесконечное реактивное сопротивление (разомкнутая цепь).
Питание от сети переменного тока серии LR
До сих пор мы рассматривали чисто индуктивную катушку, но невозможно иметь чистую индуктивность, поскольку все катушки, реле или соленоиды будут иметь определенное сопротивление, независимо от того, насколько мало связано с витками используемого провода. Тогда мы можем рассматривать нашу простую катушку как последовательное сопротивление с индуктивностью (LR).
В цепи переменного тока, которая содержит как индуктивность L и сопротивление R, напряжение V будет векторная сумма двух компонентов напряжения, V R и V L . Это означает, что ток, протекающий через катушку еще будет отставать от напряжения, но на величину меньше чем 90 ö в зависимости от значений V R и V L .
Новый фазовый угол между напряжением и током известен как фазовый угол цепи и обозначается греческим символом фи, Φ .
Чтобы получить векторную диаграмму зависимости между напряжением и током, необходимо найти эталонный или общий компонент. В последовательно соединенной цепи RL ток является общим, так как один и тот же ток течет через каждый компонент. Вектор этой эталонной величины обычно рисуется горизонтально слева направо.
Из наших руководств о резисторах и конденсаторах, мы знаем, что ток и напряжение в цепи переменного резистивного тока, оба «в фазе» и, следовательно, вектор V R рисуется с наложением на текущую или контрольную линию.
Из вышесказанного также известно, что ток «отстает» от напряжения в чисто индуктивной цепи и, следовательно, вектор V L отображается на 90 o перед опорным током и в том же масштабе, что и V R, это показано ниже.
Цепь переменного тока серии LR
На приведенной выше векторной диаграмме видно, что луч OB представляет текущую опорную линию, луч OA — это напряжение резистивного компонента, которое в фазе с током, луч OC показывает индуктивное напряжение, которое составляет 90 o перед током, поэтому видно, что ток отстает от напряжения на 90 o , луч OD дает нам результирующее или питающее напряжение в цепи. Треугольник напряжения выводится из теоремы Пифагора и имеет вид:
Треугольник сопротивления
В цепи постоянного тока отношение напряжения к току называется сопротивлением. Однако в цепи переменного тока это отношение известно как полное сопротивление Z с единицами измерения в омах. Полное сопротивление — это полное сопротивление току в «цепи переменного тока», содержащее как сопротивление, так и индуктивное сопротивление.
Если мы разделим стороны треугольника напряжения выше на ток, получим еще один треугольник, стороны которого представляют сопротивление, реактивное сопротивление и полное сопротивление катушки. Этот новый треугольник называется «Треугольник сопротивления».
Силовой треугольник индуктора переменного тока
Существует еще один тип конфигурации треугольника, который мы можем использовать для индуктивной цепи, и это «силовой треугольник». Мощность в индуктивной цепи называется реактивной мощностью или вольт-амперной реактивной, символ Var, который измеряется в вольт-амперах. В цепи переменного тока серии RL ток отстает от напряжения питания на угол Φ o .
В чисто индуктивной цепи переменного тока ток будет сдвинут по фазе на 90 o к напряжению питания. Таким образом, общая реактивная мощность, потребляемая катушкой, будет равна нулю, так как любая потребляемая мощность компенсируется генерируемой самоиндуцированной ЭДС-мощностью. Другими словами, полезная мощность в ваттах, потребляемая чистым индуктором в конце одного полного цикла, равна нулю, так как энергия берется из источника и возвращается к нему.
Реактивная мощность ( Q ) катушки может быть задана как: I 2 x X L (аналогично I 2 R в цепи постоянного тока). Затем три стороны силового треугольника в цепи переменного тока представлены кажущейся мощностью ( S ), реальной мощностью ( P ) и реактивной мощностью ( Q ), как показано.
Обратите внимание, что данный индуктор или катушка будет потреблять мощность в ваттах из — за сопротивления обмоток, создающих сопротивление Z.
Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
ЛАБОРАТОРНЫЕ РАБОТЫ
Элементы цепей переменного тока. Емкостное и индуктивное сопротивления, их зависимость от частоты переменного тока и параметров элементов
Цель: изучить зависимость емкостного и индуктивного сопротивлений от частоты переменного тока и параметров элементов.
Краткое теоретическое описание
В цепи переменного тока кроме резисторов могут использоваться катушки индуктивности и конденсаторы. Для постоянного тока катушка индуктивности имеет только активное сопротивление, которое обычно невелико (если катушка не содержит большое количество витков). Конденсатор же в цепи постоянного тока представляет "разрыв" (очень большое активное сопротивление). Для переменного тока эти элементы обладают специфическим реактивным сопротивлением, которое зависит как от номиналов деталей, так и от частоты переменного тока, протекающего через катушку и конденсатор.
1.1. Катушка в цепи переменного тока.
Рассмотрим, что происходит в цепи, содержащей резистор и катушку индуктивности. Колебания силы тока, протекающего через катушку:

вызывают падение напряжения на концах катушки в соответствии с законом самоиндукции и правилом Ленца:

т.е. колебания напряжения опережают по фазе колебания силы тока на p /2. Произведение w LIm является амплитудой колебания напряжения:

Произведение циклической частоты на индуктивность называют индуктивным сопротивлением катушки:
 (1)
(1)
поэтому связь между амплитудами напряжения и тока на катушке совпадает по форме с законом Ома для участка цепи постоянного тока:
 (2)
(2)
Как видно из выражения (1), индуктивное сопротивление не является постоянной величиной для данной катушки, а пропорционально частоте переменного тока через катушку. Поэтому амплитуда колебаний силы тока Im в проводнике с индуктивностью L при постоянной амплитуде UL напряжения убывает обратно пропорционально частоте переменного тока:
 .
.
1.2. Конденсатор в цепи переменного тока.
При изменении напряжения на обкладках конденсатора по гармоническому закону: 
заряд q на его обкладках изменяется также по гармоническому закону:
 .
.
Электрический ток в цепи возникает в результате изменения заряда конденсатора, поэтому колебания силы тока в цепи будут происходить по закону:

Видно, что колебания напряжения на конденсаторе отстают по фазе от колебаний силы тока на p /2. Произведение w CUm является амплитудой колебаний силы тока:

Аналогично тому, как было сделано с индуктивностью, введем понятие емкостного сопротивления конденсатора:
 (3)
(3)
Для конденсатора получаем соотношение, аналогичное закону Ома:
 (4)
(4)
Формулы (2) и (4) справедливы и для эффективных значений тока и напряжения.
Генератор – напряжение (эффективное) 100 В, частота 100 Гц;
Конденсатор – рабочее напряжение 400 В, емкость 10 мкФ;
Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.

 Соберите цепь показанную на рисунке 2.
Соберите цепь показанную на рисунке 2.Установите следующие значения параметров:
Генератор – напряжение (эффективное) 100 В, частота 100 Гц;
Катушка – индуктивность 50 мГн;
Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.
3. Контрольные вопросы.
3.1. Почему емкостное сопротивление уменьшается с увеличением частоты переменного ток а, индуктивное сопротивление – увеличивается?
3.2. Каковы разницы фаз между током и напряжением для катушки и конденсатора?
3.3. В каких единицах измеряются емкостное и индуктивное сопротивления?

