Напряженность магнитного полянеобходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах. Напряженность магнитного поля характеризует магнитное поле в вакууме.
Напряженность магнитного поля (формула)векторная физическая величина, равная:
Напряженность магнитного поля в СИ – ампер на метр (А/м).
Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поляв данной точке, то можно определить индукцию поля в этой точке.
Напряженность магнитного поля зависит только от силы тока, протекающего по проводнику, и его геометрии.
Намагниченность — характеристика магнитного состояния макроскопического физического тела.
Однородно намагниченное тело:
Любое вещество, помещенное в магнитное поле, приобретает некоторый магнитный момент. Намагниченность J – это магнитный момент единицы объема.
В несильных полях намагниченность прямо пропорциональна напряженности поля, вызывающего намагничивание: :
Если же тело намагничено неоднородно (состоит из нескольких частей), то намагниченность определяется для каждого физически малого объема dV
МАГНИТНАЯ ВОСПРИИМЧИВОСТЬ , величина, характеризующая связь намагниченности вещества с магнитным полем в этом веществе. М. в. 
в статич. полях равна отношению намагниченности вещества М к напряжённости Н намагничивающего поля: 
; 
– величина безразмерная. М. в., рассчитанная на 1 кг (или 1 г) вещества, наз. удельной ( 
, где р – плотность вещества), а М. в. одного моля – молярной (или атомной): 
, где т – молекулярная масса вещества. С магнитной проницаемостью 
. в. в статич. полях (статич. М. в.) связана соотношениями: 
(в ед. СГС), 
(в ед. СИ). М. в. может быть как положительной, так и отрицательной. Отрицательной М. в. обладают диамагнетики (ДМ), они намагничиваются против поля; положительной – парамагнетики (ПМ) и ферромагнетики (ФМ), они намагничиваются по полю. М. в. ДМ и ПМ мала по абс. величине 
, она слабо зависит от Н и то лишь в области очень сильных полей (и низких темп-р).
Физическая величина, показывающая, во сколько раз индукция 
магнитного поля в однородной среде отличается по модулю от индукции 
магнитного поля в вакууме, называется магнитной проницаемостью:
 |
18.Диамагнетики,парамагнетики,ферромагнетики.
Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля. Поэтому у парамагнетиковμ > 1, а у диамагнетиков μ –5 , у хлористого железа (FeCl3) μ – 1 ≈ 2,5·10 –3 . К парамагнетикам относятся также платина, воздух и многие другие вещества. К диамагнетикам относятся медь(μ – 1 ≈ –3·10 –6 ), вода (μ – 1 ≈ –9·10 –6 ), висмут (μ – 1 ≈ –1,7·10 –3 ) и другие вещества. Образцы из пара- и диамагнетика, помещенные в неоднородное магнитное поле между полюсами электромагнита, ведут себя по-разному – парамагнетики втягиваются в область сильного поля, диамагнетики – выталкиваются (рис. 1.19.1).
 |
| Рисунок 1.19.1. Парамагнетик (1) и диамагнетик (2) в неоднородном магнитном поле |
Пара- и диамагнетизм объясняется поведением электронных орбит во внешнем магнитном поле. У атомов диамагнитных веществ в отсутствие внешнего поля собственные магнитные поля электронов и поля, создаваемые их орбитальным движением, полностью скомпенсированы. Возникновение диамагнетизма связано с действием силы Лоренца на электронные орбиты. Под действием этой силы изменяется характер орбитального движения электронов и нарушается компенсация магнитных полей. Возникающее при этом собственное магнитное поле атома оказывается направленным против направления индукции внешнего поля.
Вещества, способные сильно намагничиваться в магнитном поле, называются ферромагнетиками. Магнитная проницаемость ферромагнетиков по порядку величины лежит в пределах 10 2 –10 5 . Например, у стали μ ≈ 8000, у сплава железа с никелем магнитная проницаемость достигает значений 250000.
К рассматриваемой группе относятся четыре химических элемента: железо, никель, кобальт, гадолиний. Из них наибольшей магнитной проницаемостью обладает железо. Поэтому вся эта группа получила название ферромагнетиков.
Ферромагнетиками могут быть различные сплавы, содержащие ферромагнитные элементы. Широкое применение в технике получили керамические ферромагнитные материалы – ферриты.
Для каждого ферромагнетика существует определенная температура (так называемая температура или точка Кюри), выше которой ферромагнитные свойства исчезают, и вещество становится парамагнетиком. У железа, например, температура Кюри равна 770 °C, у кобальта 1130 °C, у никеля 360 °C.
Ферромагнитные материалы делятся на две большие группы – на магнито-мягкие и магнито-жесткие материалы. Магнито-мягкие ферромагнитные материалы почти полностью размагничиваются, когда внешнее магнитное поле становится равным нулю. К магнито-мягким материалам относится, например, чистое железо, электротехническая сталь и некоторые сплавы. Эти материалы применяются в приборах переменного тока, в которых происходит непрерывное перемагничивание, то есть изменение направления магнитного поля (трансформаторы, электродвигатели и т. п.).
Магнито-жесткие материалы в значительной мере сохраняют свою намагниченность и после удаления их из магнитного поля. Примерами магнито-жестких материалов могут служить углеродистая сталь и ряд специальных сплавов. Магнито-жесткие метериалы используются в основном для изготовления постоянных магнитов.
Магнитная проницаемость μ ферромагнетиков не является постоянной величиной; она сильно зависит от индукции B0 внешнего поля. Типичная зависимость μ (B0) приведена на рис. 1.19.2. В таблицах обычно приводятся значения максимальной магнитной проницаемости.
Последнее изменение этой страницы: 2016-06-23; Нарушение авторского права страницы
Она необходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах.Напряженность магнитного поляхарактеризует магнитное поле в вакууме.
Напряженность магнитного поля (формула) векторная физическая величина, равная:
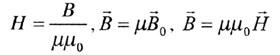
Где u0- магнитная постоянная.
Гн/м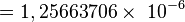
Н/А².
Напряженность магнитного поляв СИ – ампер на метр (А/м).
Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поля в данной точке, то можно определить индукцию поля в этой точке.
Напряженность магнитного полязависит только от силы тока, протекающего по проводнику, и его геометрии.
С помощью следующей формулы, мы можем сформулировать теорему о циркуляции вектора H:циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, охватываемых этим контуром.
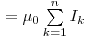
Напряженность магнитного поля является аналогом электрического смещения.
23)Условия для h и b на границе раздела двух изотропных магнетиков :
Рассмотрим поведение линий векторов магнитной индукции и напряжённости магнитного поля при переходе через границу раздела двух магнетиков.
Представим себе две однородные, изотропные полубесконечные среды с магнитными проницаемостями 
и
, имеющие плоскую горизонтальную границу раздела. Пусть оба магнетика находятся в однородном внешнем магнитном поле. Чтобы понять, как происходит преломление линий векторов магнитной индукции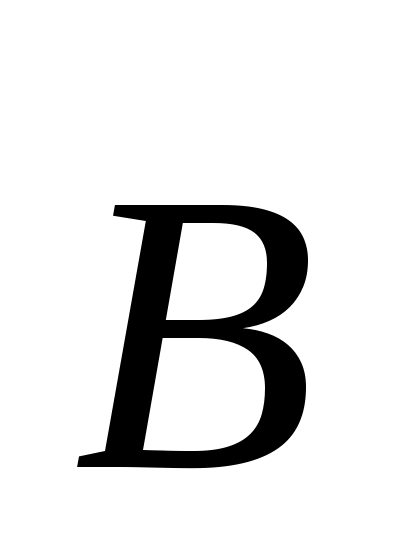
и напряжённости магнитного поля
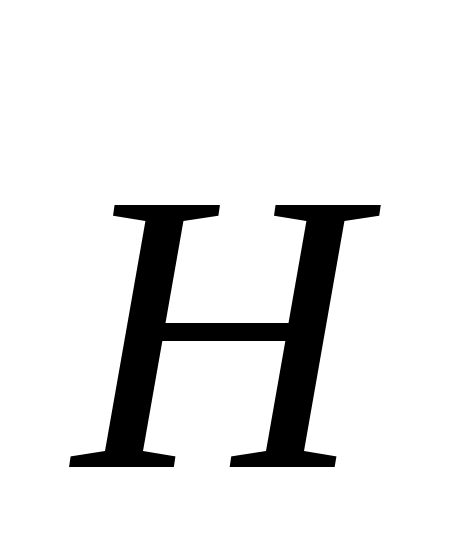через эту границу, рассмотрим проекции этих векторов на саму границу и на направление, перпендикулярное границе и назовём их касательными и нормальными составляющими, соответственно.
Пусть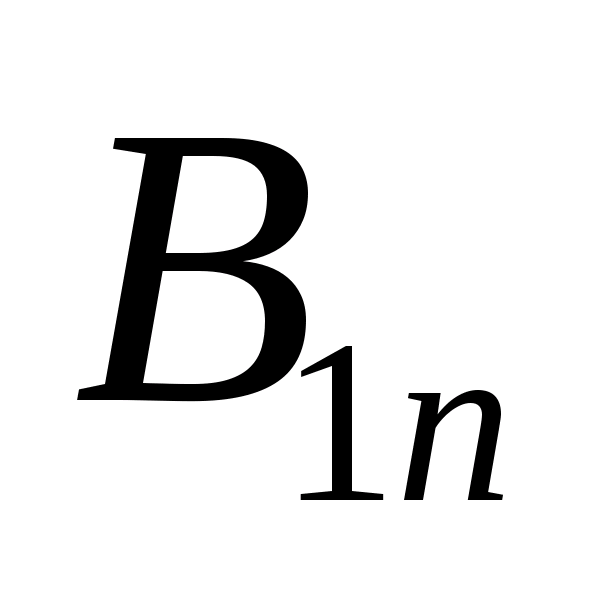 
и
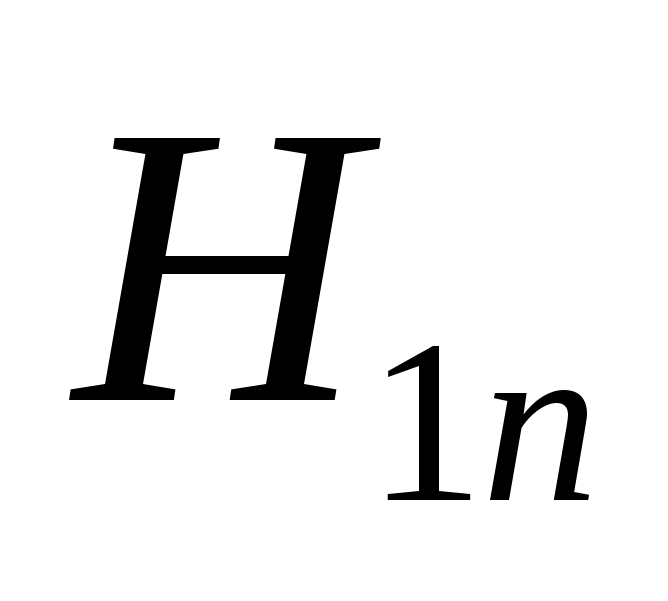─ нормальные составляющие векторов магнитной индукции и напряжённости магнитного поля, а
и
─ касательные составляющие тех же векторов в верхней среде, имеющей магнитную проницаемость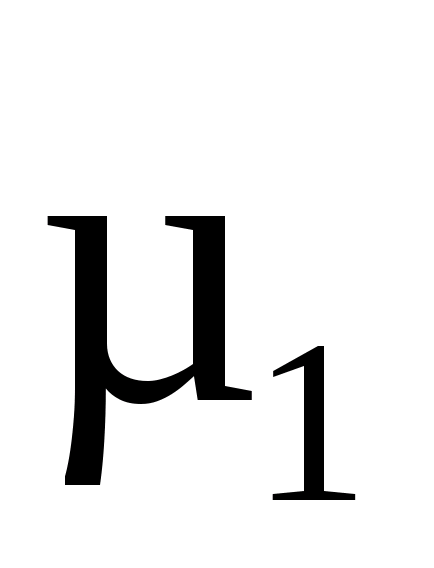
. Аналогичные величины в нижней среде, имеющей магнитную проницаемость
, обозначим
.
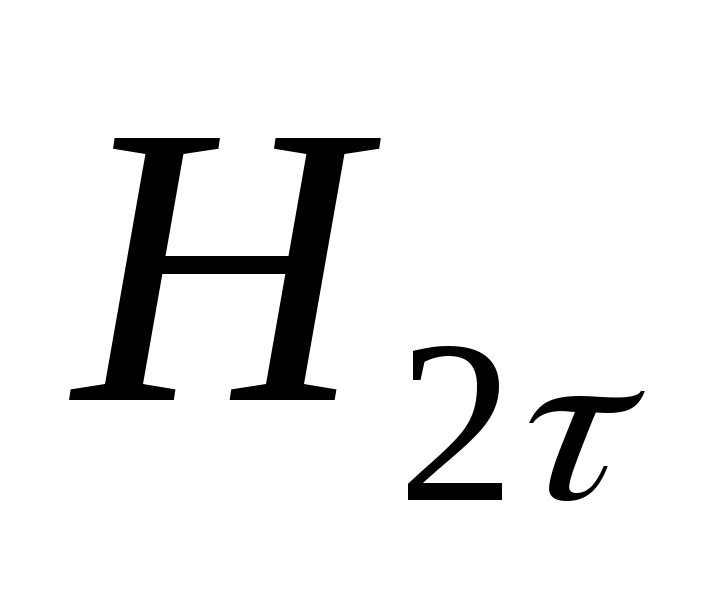Представим себе, что линии вектора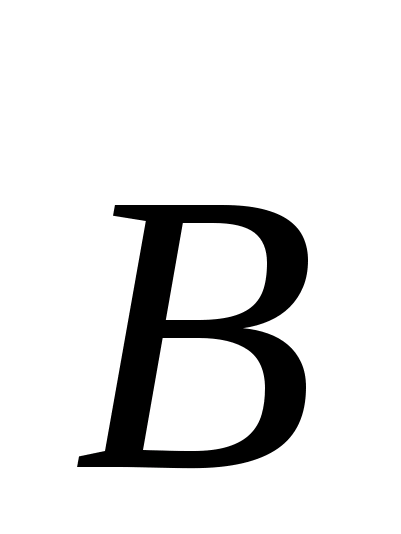 
преломляются при переходе через границу раздела так, как показано на рис. 1. Рассмотрим при этом преломление пока только одной силовой линии.
Поместим на границе раздела воображаемую цилиндрическую поверхность с высотой h значительно меньшей радиусов оснований S1 и S2, лежащих по обе стороны от границы раздела и параллельных ей. На рисунке также показана нормаль 
к границе раздела и к обоим основаниям.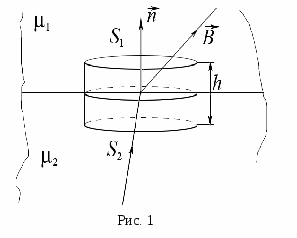
Запишем теорему Гаусса для магнитной индукции:
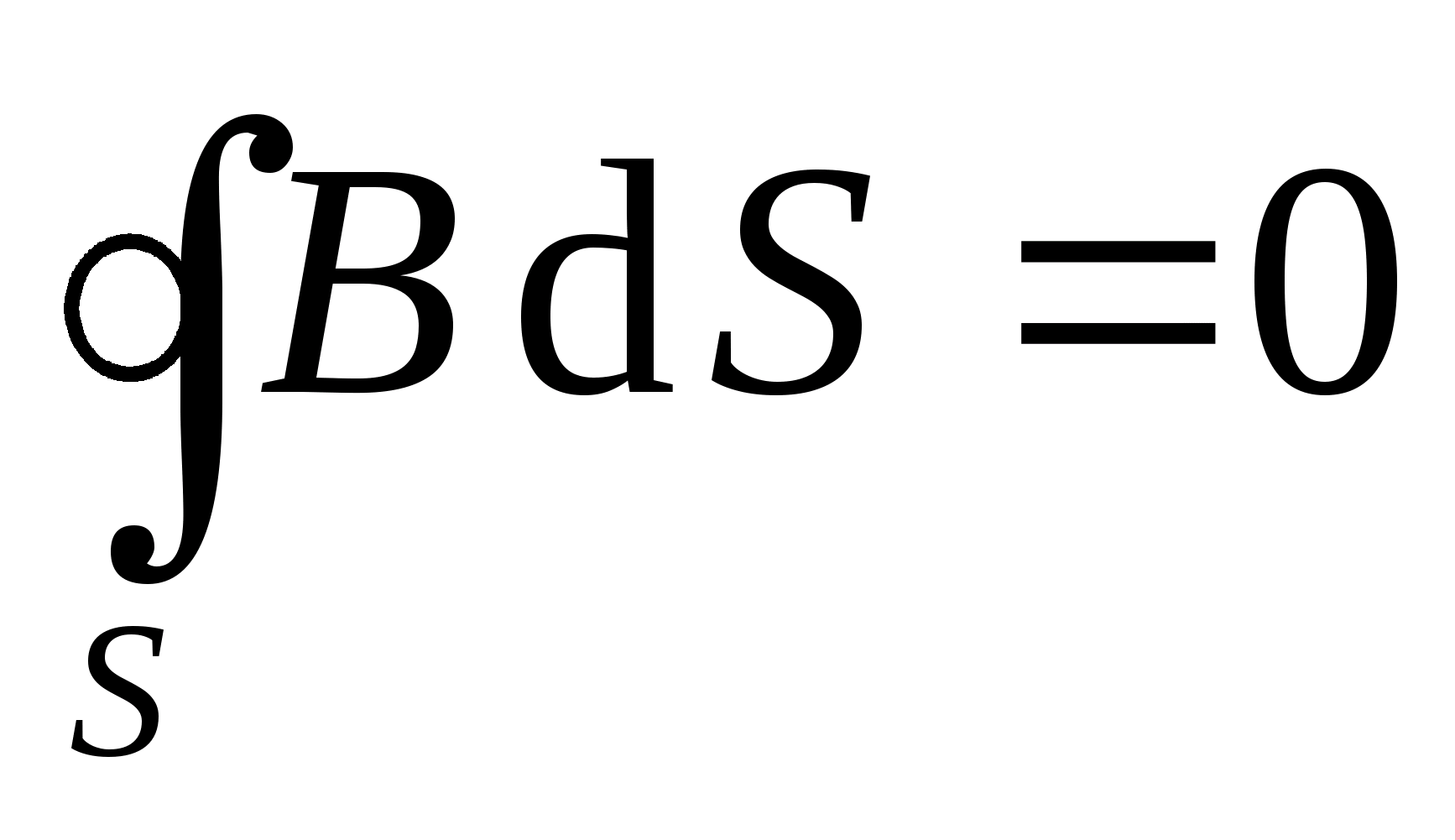или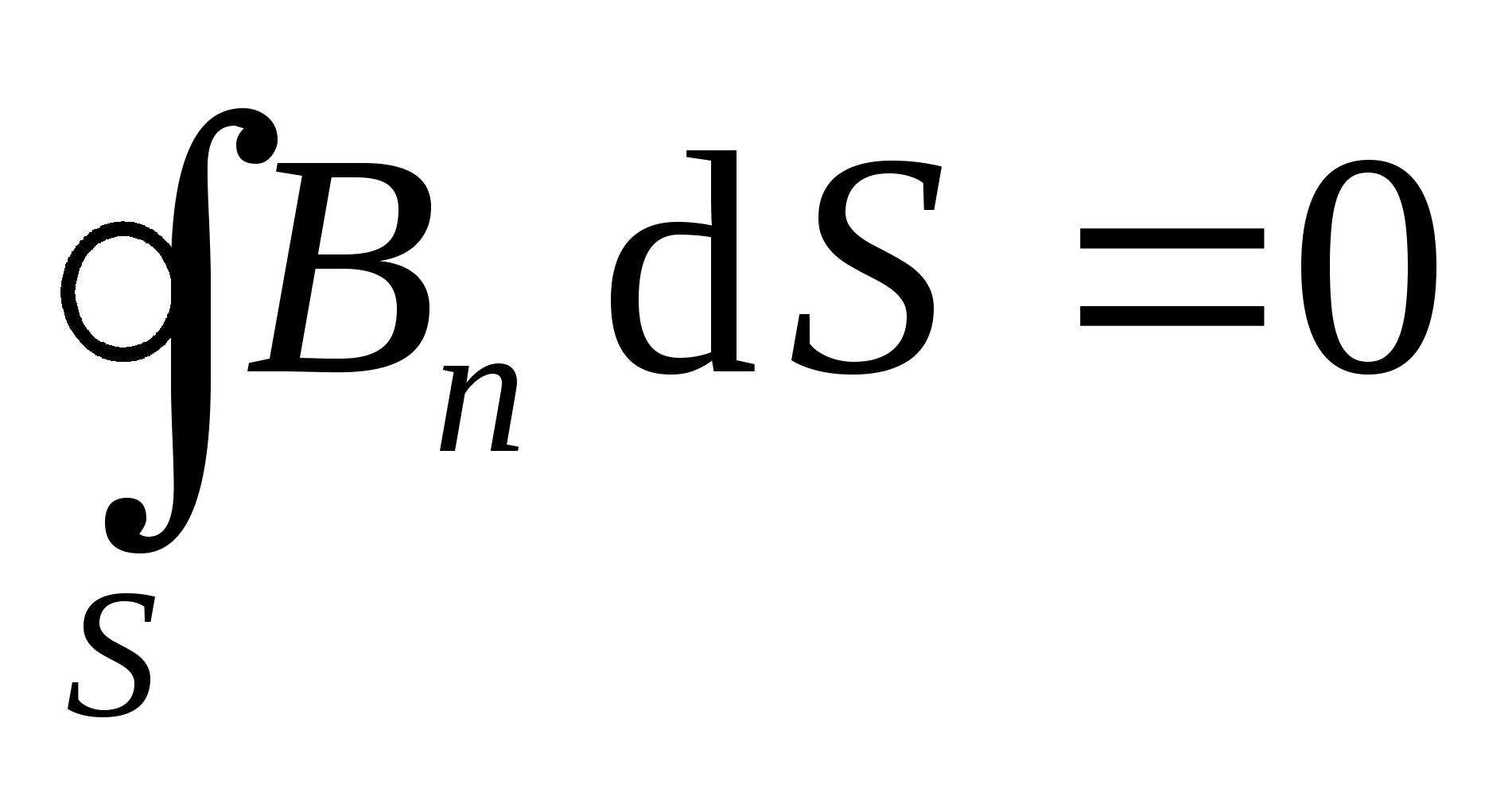 
,
где S ─ замкнутая поверхность, состоящая из боковой поверхности и оснований цилиндра.
Этот круговой интеграл можно разбить на 3 интеграла, каждый из которых равен потоку через верхнее и нижнее основания и боковую поверхность
.
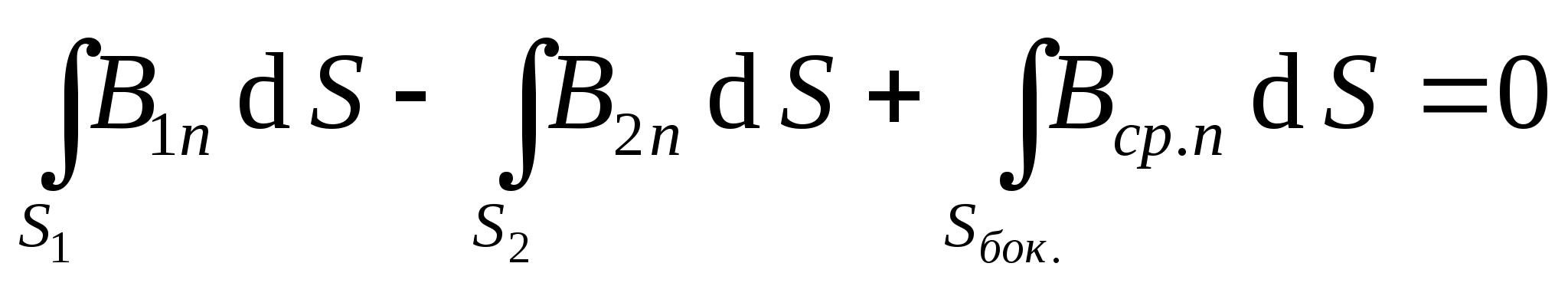Здесь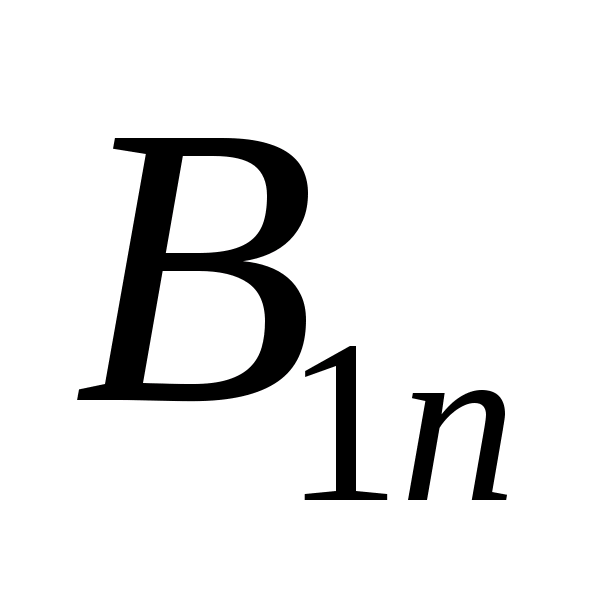 
и
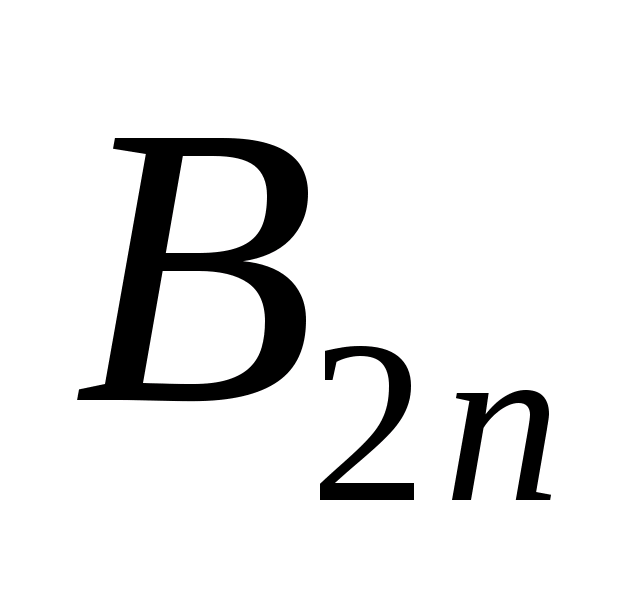─ нормальные составляющие векторов магнитной индукции в верхнем и нижнем магнетиках, соответственно,
─ среднее значение проекции вектора магнитной индукции на нормаль к боковой поверхности.
Поскольку оба магнетика помещены в однородное внешнее магнитное поле, то все интегралы можно заменить соответствующими произведениями:
.
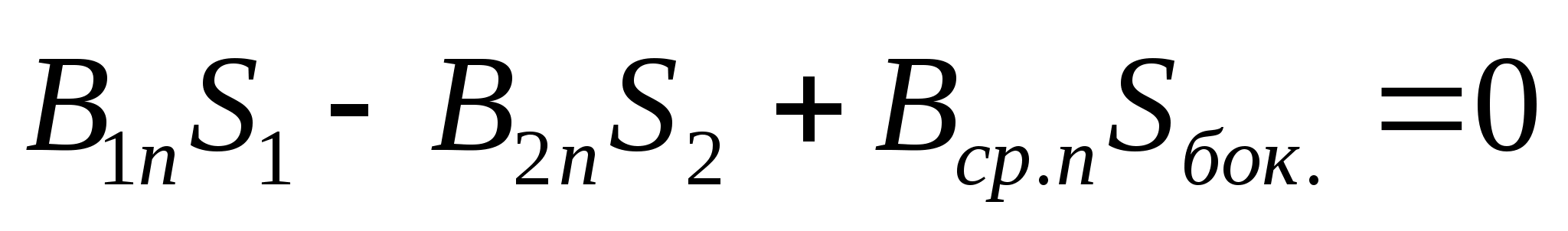Как и в предыдущей формуле, здесь первая составляющая магнитного потока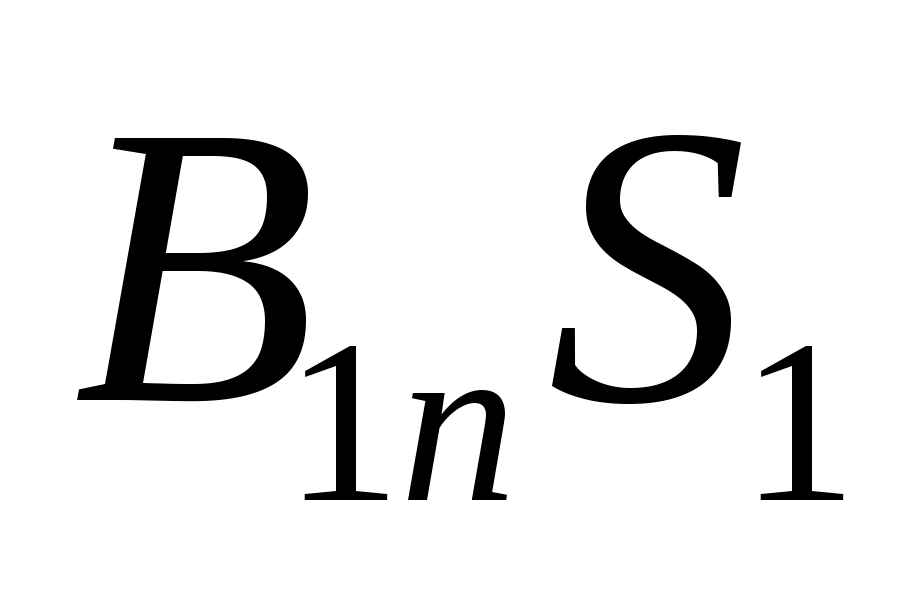 
положительна, так как силовые линии выходят из поверхности
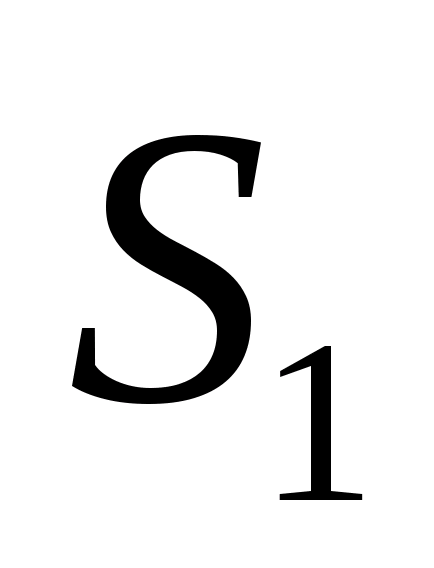, а вторая составляющая
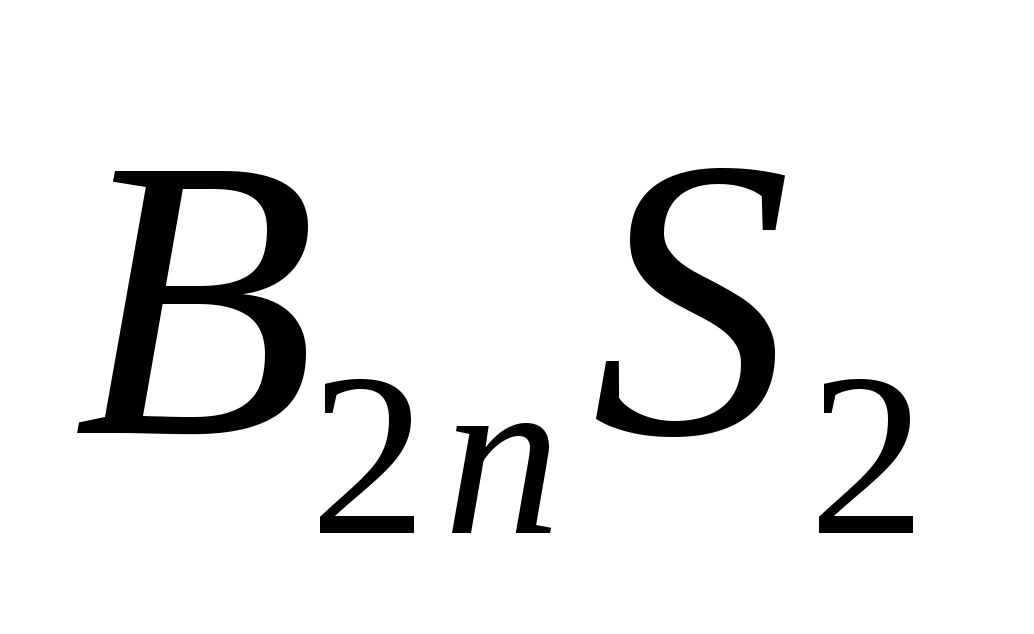─ отрицательна, так как силовые линии входят в поверхность
(вектора
и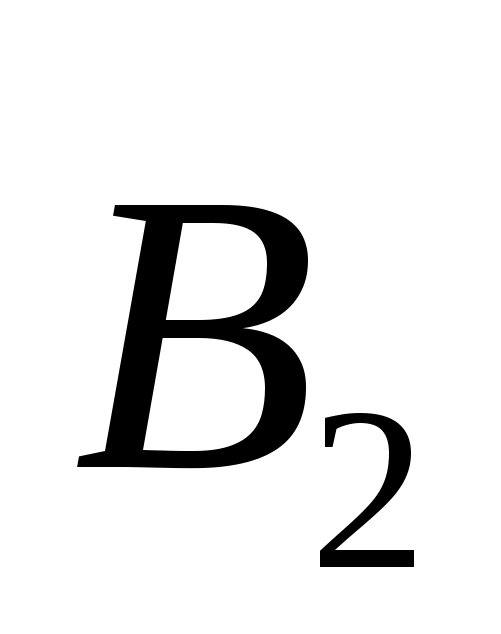
спроектированы на одну и ту же нормаль). Третьей составляющей ─
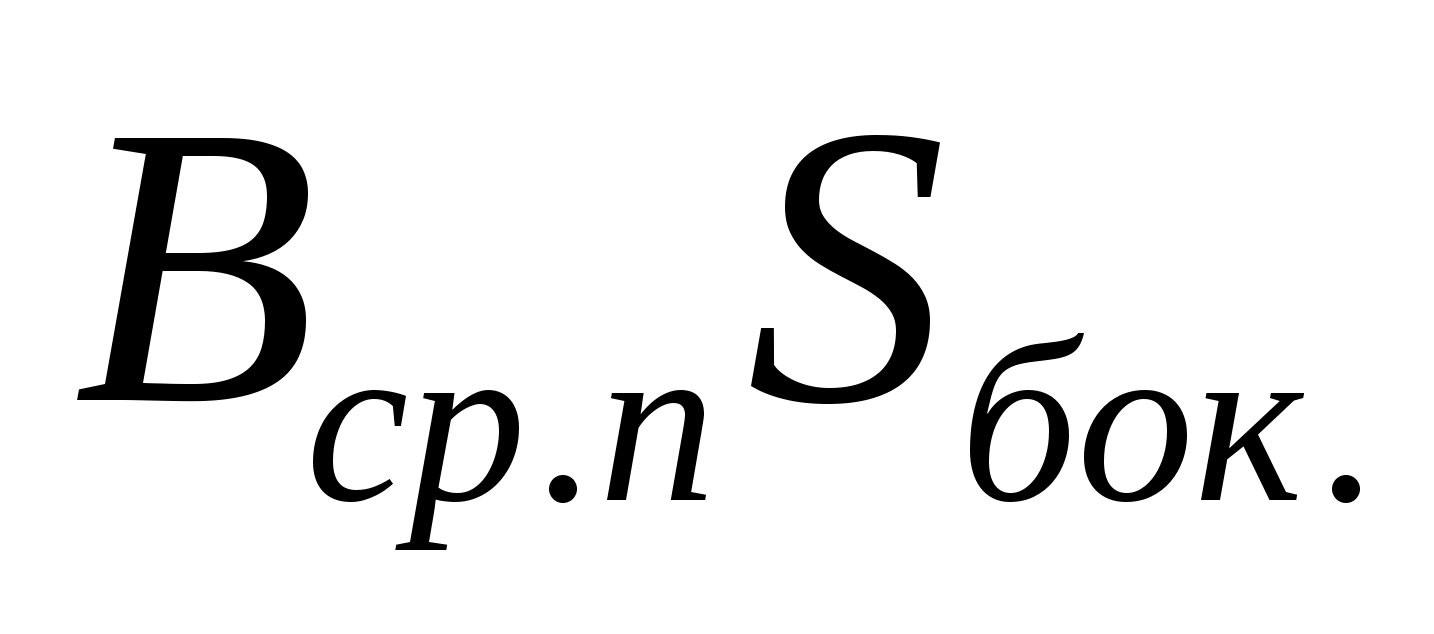можно пренебречь, так как высота цилиндра выбрана очень малой по сравнению с радиусами оснований, т. е., если
, то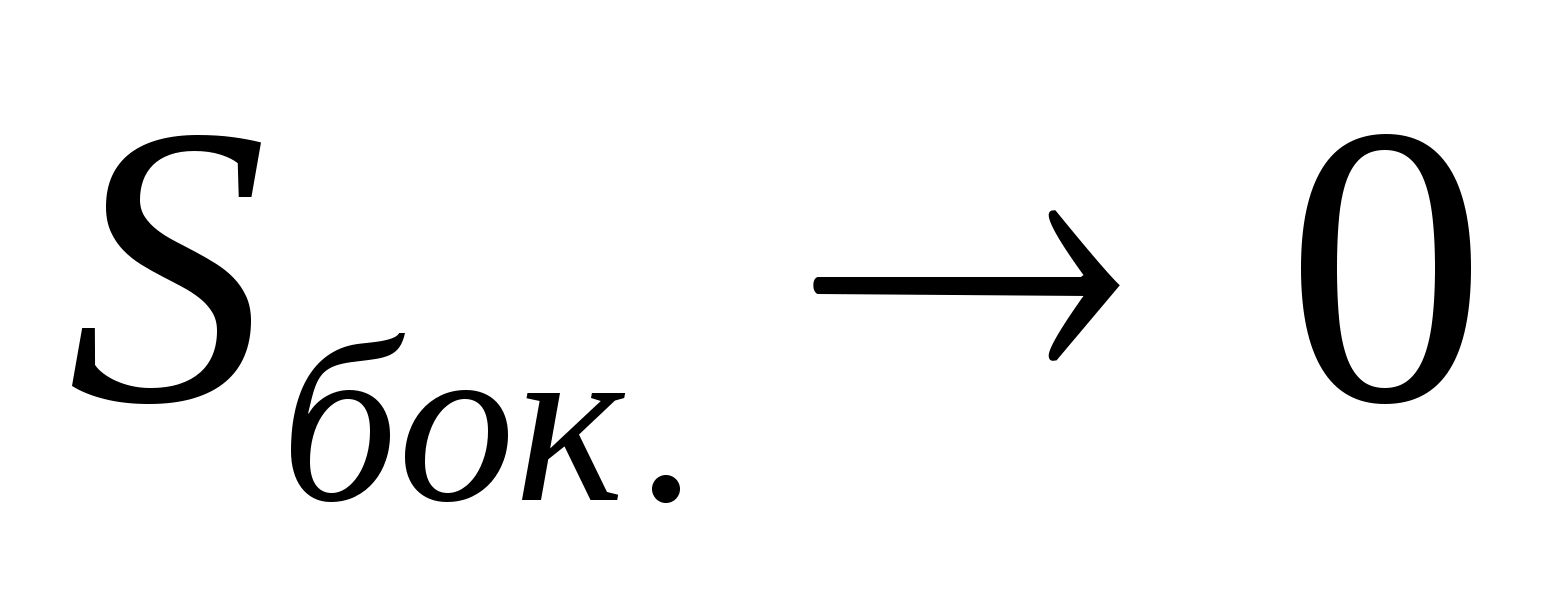
.
Учитывая, что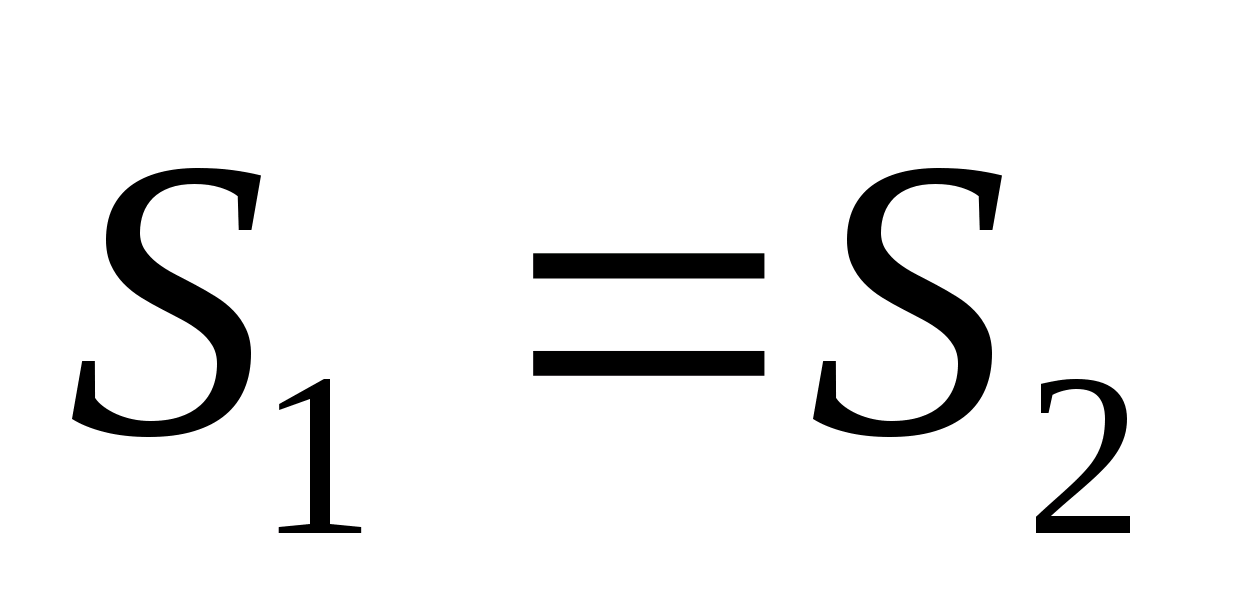 
, получим:
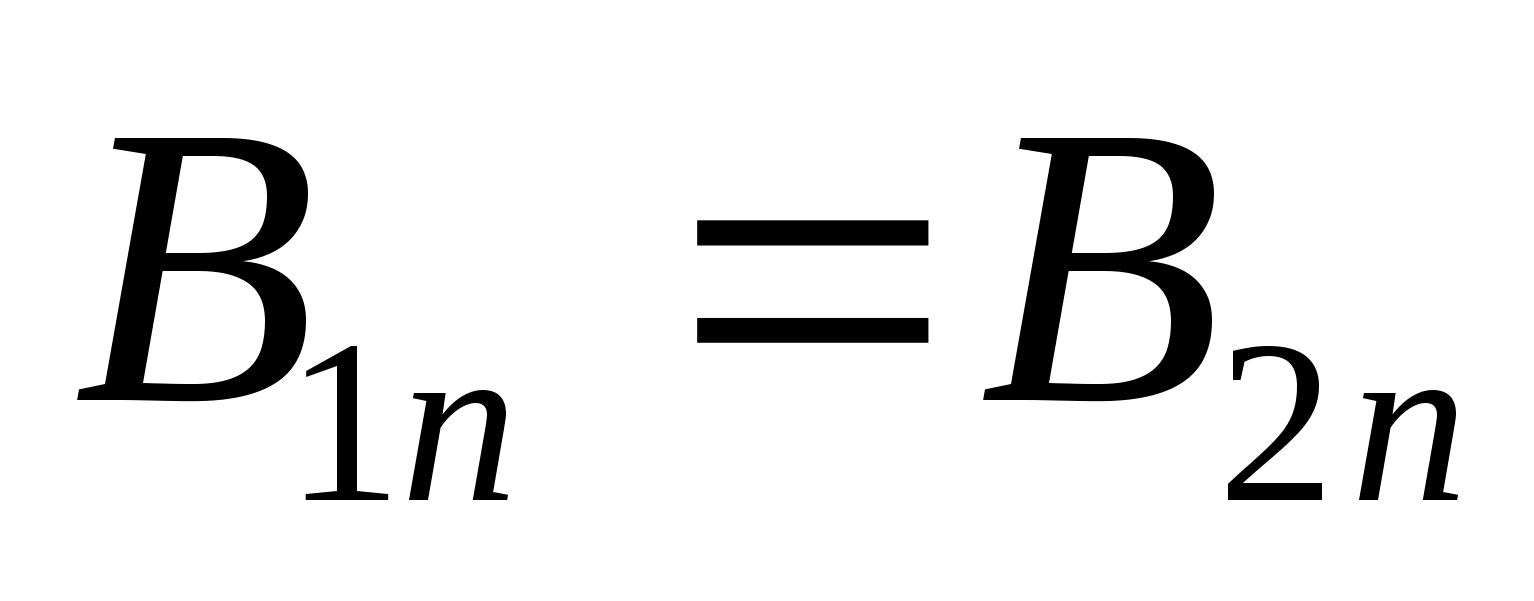. (1)
Используя связь магнитной индукции и напряжённости магнитного поля
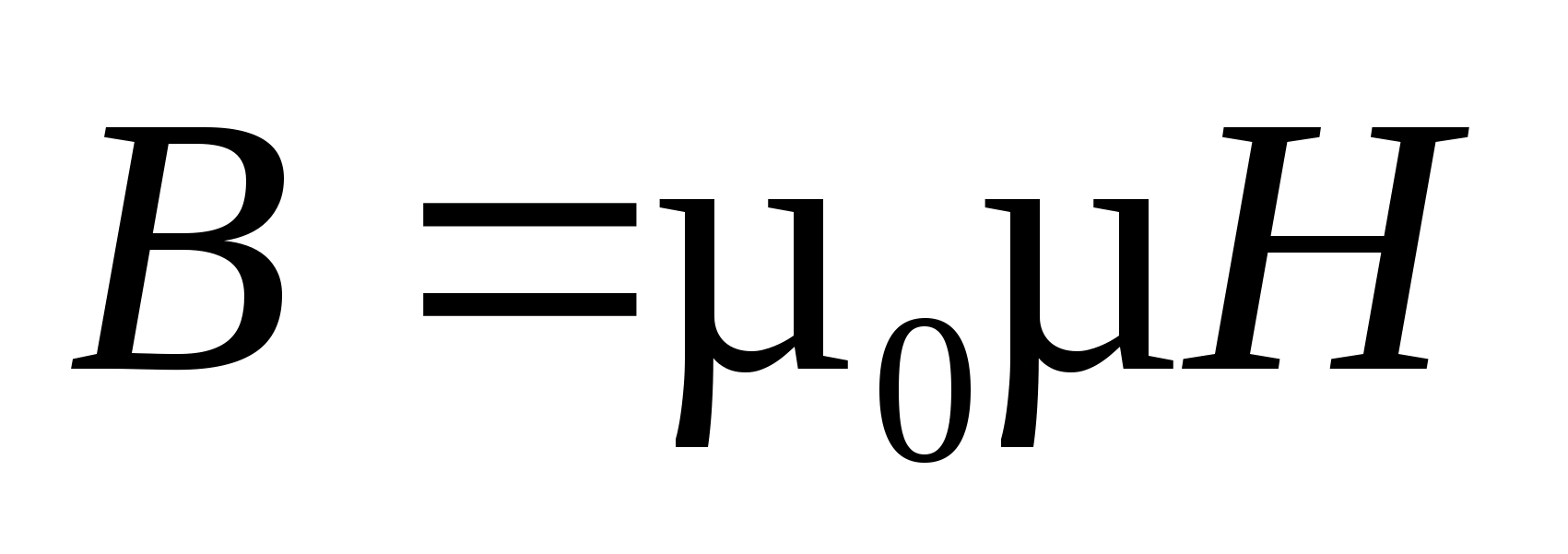, (2)
и, применяя её для первого и второго магнетиков в формуле (1), получим:
.
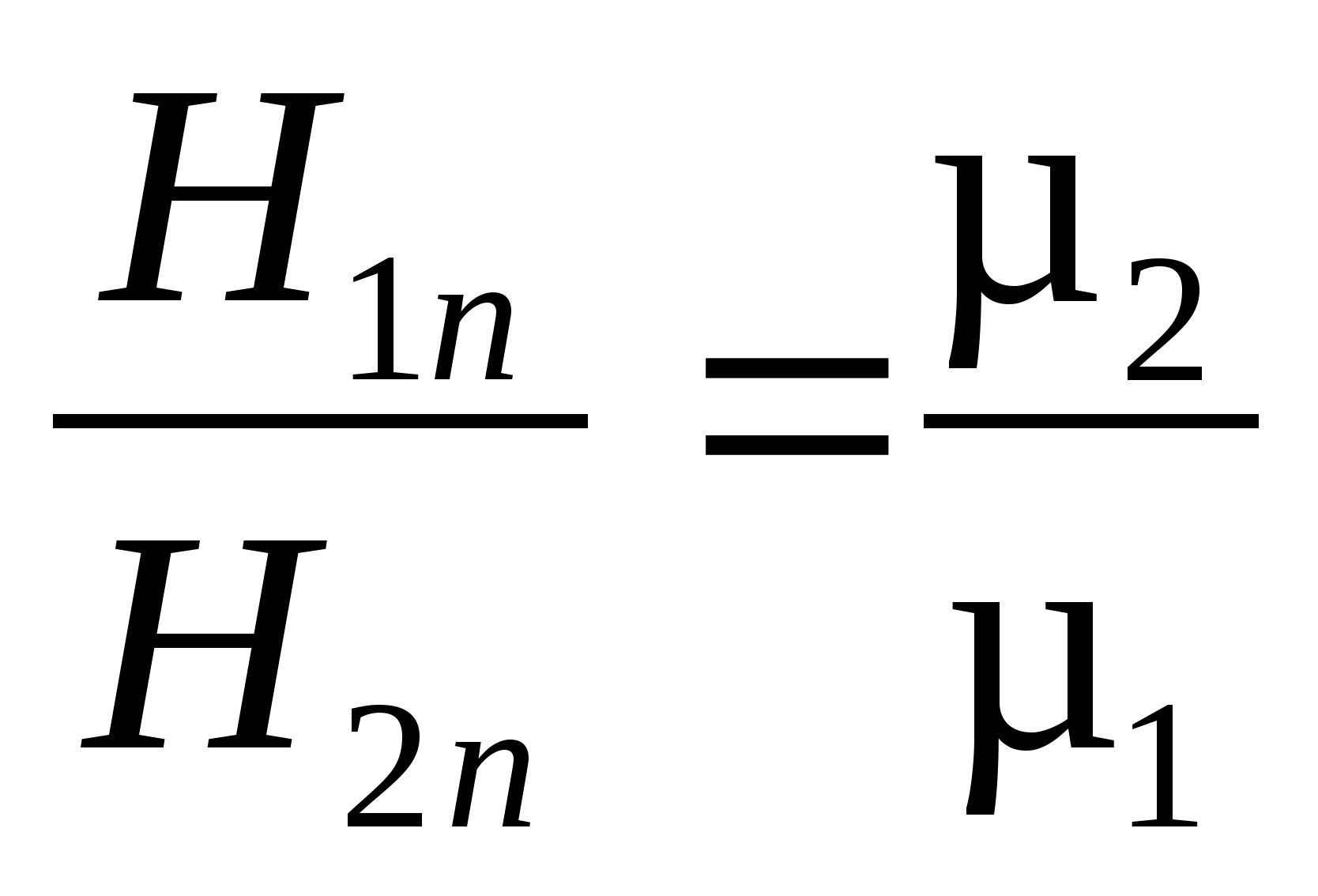. (3)
Напряженность магнитного полянеобходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах. Напряженность магнитного поля характеризует магнитное поле в вакууме.
Напряженность магнитного поля [H] – это отношение магнитной индукции к магнитной проницаемости среды
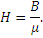
Напряженность магнитного поля – величина векторная. За единицу измерения напряженности магнитного поля в Международной системе единиц принят ампер на метр.
Напряженность магнитного поля (формула)векторная физическая величина, равная:
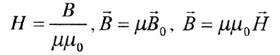
Напряженность магнитного поля в СИ – ампер на метр (А/м).
Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поляв данной точке, то можно определить индукцию поля в этой точке.
Напряженность магнитного поля зависит только от силы тока, протекающего по проводнику, и его геометрии.
Обобщая экспериментальные данные французских физиков Био и Савара, Лаплас (французский математик) предложил формулу, по которой можно вычислять напряженность поля, создаваемого элементом тока в точке, расположенной от этого элемента на расстоянии r.
- Теорема Ампера о циркуляции магнитного поля:
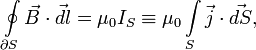
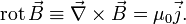
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10611 – 
| 7337 – 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно