Выведите формулу для периода колебаний физического маятника

43. Дайте определение и выведите формулу периода колебаний физического маят­ника.

В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятники.

Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.

Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим. При отклонении от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен:

,

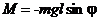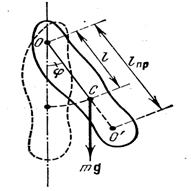
где m – масса маятника, l – расстояние между точкой подвеса О и центром инерции C маятника. Знак “ – ” имеет тоже значение, что и в случае квазиупругой силы . Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой I, можно написать основной закон динамики:

В случае малых колебаний это уравнение переходит в уже известное нам уравнение незатухающих гармонических колебаний:

,

где через обозначена в данном случае следующая величина:

Из этого уравнения следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания. При этом период колебаний физического маятника определяется выражением:

Проведенное выше рассмотрение имеет место и для математического маятника. В этом случае маятник представляет собой материальную точку, момент инерции которой относительно оси, проходящей через точку подвеса, равен . С учетом этого, получаем формулу для периода колебаний математического маятника:

Для физического маятника вводится понятие приведенной длины . Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника, т.е. .

Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см. точку на рисунке). Можно показать, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания точка подвеса становится новым центром качания.

Получите дифференциальное уравнение затухающих гармонических колебаний.

45. По какому закону изменяется колеблющаяся величина при затухающих гармо­нических колебаниях? Приведите график зависимости

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ – конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Физическим маятником называется твердое тело, находящееся в поле силы тяжести и имеющее горизонтальную ось вращения, не проходящую через центр тяжести тела.

Пусть — масса тела, J — его момент инерции относительно оси вращения — расстояние от центра тяжести до оси вращения (рис. 36). Выведенное из положения равновесия, тело будет вращаться либо совершать колебательное движение. В обоих случаях дифференциальное уравнение движения имеет один и тот же вид (силами трения пренебрегаем):

Пусть начальные условия таковы, что угол все время остается малым (максимальное отклонение от вертикали не превышает ). Тогда можно приближенно принять (в радианах) и рассматривать более простое уравнение:

или, что то же, уравнение

Это уравнение называется дифференциальным уравнением малых колебаний физического маятника. Из него следует, что малые колебания физического маятника являются гармоническими колебаниями частоты

Амплитуда и фаза колебаний будут определяться начальным отклонением и начальной угловой скоростью физического маятника.

Вопросы для самопроверки

1. Что называется моментом количества движения материальной точки?

2. Что называется кинетическим моментом механической системы относительно данного центра, данной оси?

3. Приведите общие формулы для определения кинетического момента механической системы (относительно данного центра, данной оси).

4. Приведите математическую запись теоремы об изменении кинетического момента. Дайте словесную формулировку теоремы.

5. В каких случаях кинетический момент системы или его проекция на ось остаются постоянными при движении системы?

6. Какие координатные оси называются осями Кенига?

7. Приведите общую формулу для определения кинетического момента твердого тела относительно данного неподвижного центра?

8. Как вычисляется кинетический момент тела при его поступательном и вращательном движениях?

9. Как составляются дифференциальные уравнения движения тела при его поступательном движении? При вращении вокруг неподвижной оси? При плоскопараллельном движении?

10. Что называется физическим маятником? Как определяется период его малых колебаний?

Упражнения

1. Материальная точка М массы движется по окружности радиуса R согласно уравнению (рис. 37). Вычислить и построить количество движения и момент количества движения точки при .

2. Сплошной однородный диск массы и радиуса R вращается вокруг своей оси согласно уравнению . Найти кинетический момент диска относительно оси вращения.

3. Решить в указанном порядке следующие задачи из сборника И.В. Мещерского 1981 г. издания: 28.4; 37.1; 37.56; 37.43; 37.5; 37.6; 37.16.

Физическим маятником называется твердое тело, находящееся в поле силы тяжести и имеющее горизонтальную ось вращения, не проходящую через центр тяжести тела.

Пусть — масса тела, J — его момент инерции относительно оси вращения — расстояние от центра тяжести до оси вращения (рис. 36). Выведенное из положения равновесия, тело будет вращаться либо совершать колебательное движение. В обоих случаях дифференциальное уравнение движения имеет один и тот же вид (силами трения пренебрегаем):

Пусть начальные условия таковы, что угол все время остается малым (максимальное отклонение от вертикали не превышает ). Тогда можно приближенно принять (в радианах) и рассматривать более простое уравнение:

или, что то же, уравнение

Это уравнение называется дифференциальным уравнением малых колебаний физического маятника. Из него следует, что малые колебания физического маятника являются гармоническими колебаниями частоты

Амплитуда и фаза колебаний будут определяться начальным отклонением и начальной угловой скоростью физического маятника.

Вопросы для самопроверки

1. Что называется моментом количества движения материальной точки?

2. Что называется кинетическим моментом механической системы относительно данного центра, данной оси?

3. Приведите общие формулы для определения кинетического момента механической системы (относительно данного центра, данной оси).

4. Приведите математическую запись теоремы об изменении кинетического момента. Дайте словесную формулировку теоремы.

5. В каких случаях кинетический момент системы или его проекция на ось остаются постоянными при движении системы?

6. Какие координатные оси называются осями Кенига?

7. Приведите общую формулу для определения кинетического момента твердого тела относительно данного неподвижного центра?

8. Как вычисляется кинетический момент тела при его поступательном и вращательном движениях?

9. Как составляются дифференциальные уравнения движения тела при его поступательном движении? При вращении вокруг неподвижной оси? При плоскопараллельном движении?

10. Что называется физическим маятником? Как определяется период его малых колебаний?

Упражнения

1. Материальная точка М массы движется по окружности радиуса R согласно уравнению (рис. 37). Вычислить и построить количество движения и момент количества движения точки при .

2. Сплошной однородный диск массы и радиуса R вращается вокруг своей оси согласно уравнению . Найти кинетический момент диска относительно оси вращения.

3. Решить в указанном порядке следующие задачи из сборника И.В. Мещерского 1981 г. издания: 28.4; 37.1; 37.56; 37.43; 37.5; 37.6; 37.16.