Циркуляцией вектора В по заданному замкнутому контуру называется интеграл
, (9.1)
где dl – вектор элементарной длины контура, направленной вдоль обхода контура, Вl =Вcosα– составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода), α – угол между векторами В и dl.
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной μо на алгебраическую сумму токов охватываемых этим контуром:
, (9.2)
где n – число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.
Например, для системы токов, изображенных на рис.12, 
.
Выражение (9.2) справедливо только для поля в вакууме, поскольку для поля в веществе
Рис.12. необходимо согласно вышеизложенной гипотезе Ампера, учитывать микротоки (молекулярные токи).
Закон полного тока для магнитного поля в веществе является обобщением вышеприведенного закона с учетом как макротоков, так и микротоков:
, (9.3)
где I и I о – соответственно алгебраические суммы сил макротоков (токов проводимости) и микротоков, охватываемых заданных контуром. Таким образом, циркуляция вектора магнитной индукции В по замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор В, характеризует результирующее поле микро- и макротоков и поэтому линии вектора магнитной индукции не имеют источников и являются замкнутыми.
Как показывает (1.4), магнитное поле макротоков описывается вектором напряженности Н, (В=μоμН). Следовательно, циркуляция вектора напряженности Н магнитного поля равна алгебраической сумме сил токов проводимости, охватываемых этим контуром
. (9.4)
Это выражение представляет собой теорему о циркуляции вектора Н.
Между циркуляции векторов Е и Всуществует принципиальное различие. Циркуляция вектора Еэлектростатического поля всегда равна нулю, т.е. электростатическое поле является потенциальным. Циркуляции векторов ВиН магнитного поля нулю не равны. Такое поле называется вихревым, непотенциальным. Следовательно магнитное поле непотенциально.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8815 – 
| 7171 – 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Закон полного тока для магнитного поля в вакууме состоит в том, что циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна произведению магнитной постоянной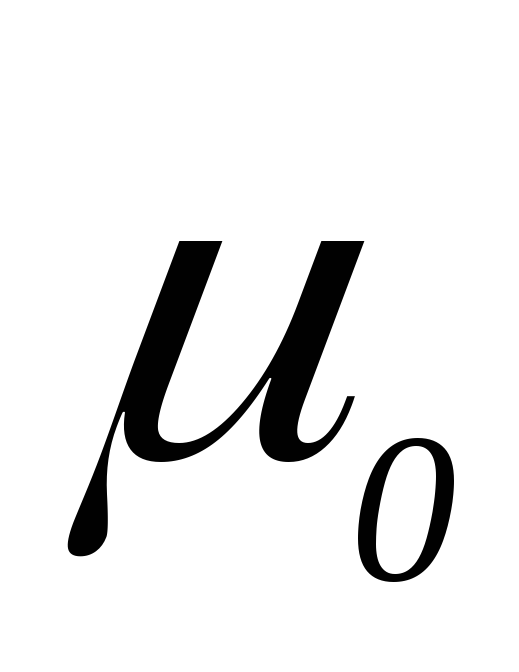 
на алгебраическую сумму токов, охватываемых этим контуром. Запишем его:
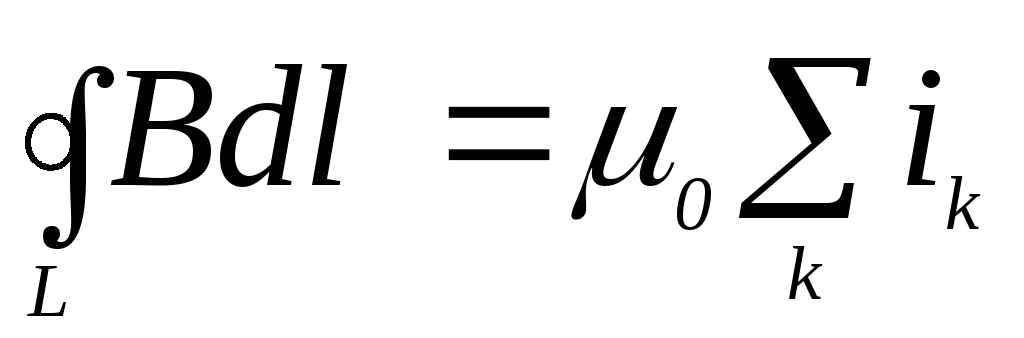. (5.4)
Обобщим закон полного тока на случай магнитного поля в веществе. Для этого нужно учесть все токи, охватываемые контуром: как макротоки (токи проводимости), так и микротоки (молекулярные токи).
Тогда для магнитного поля в веществе имеем:
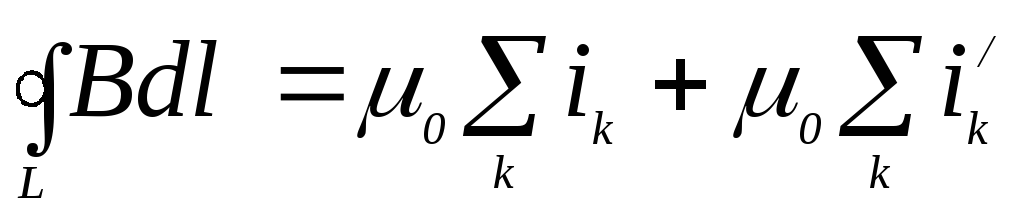. (5.5)
Здесь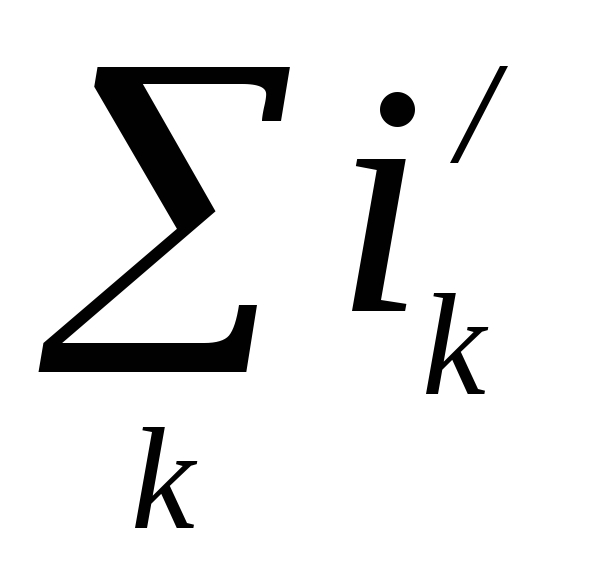 
– алгебраическая сумма молекулярных токов, охватываемых замкнутым контуромL. Выразим ее через вектор намагниченности.
Р
ассмотрим произвольный замкнутый контурL. Контур охватывает множество молекулярных токов (рис.5.2). Но вклад в сумму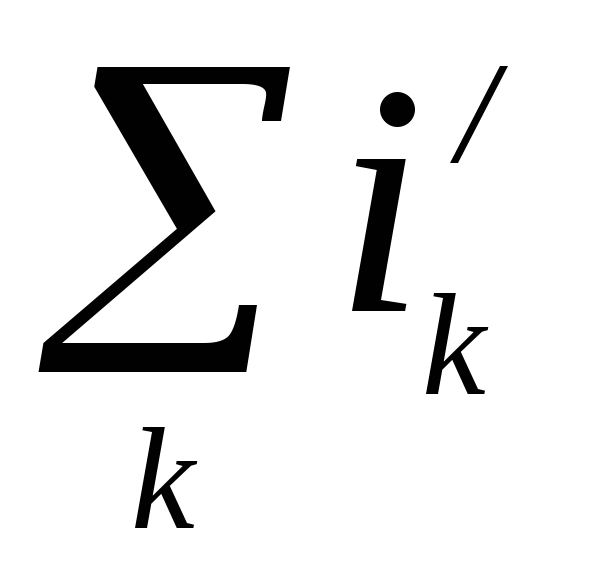 
будут вносить только те токи, плоскость которых пересекается контуром (1, 2, 3, 4).
Пусть некоторый элемент контура 
образует с вектором намагниченности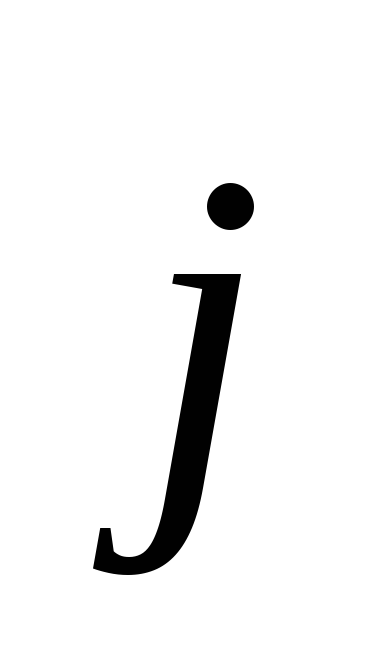
угол
(рис.5.3). Тогда элемент
пересекает только те молекулярные токи, центры которых попали внутрь косого цилиндра, основания которого равныS / (площади, охватываемой отдельным молекулярным током). Объём этого цилиндра равен
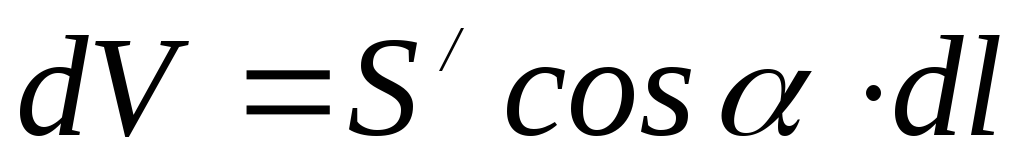. (5.6)
Число молекулярных токов, охватываемых элементом 
, равно:
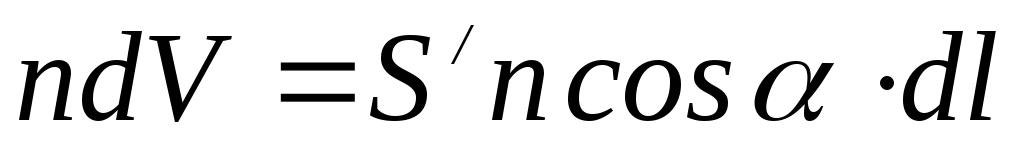. (5.7)
Здесь n – концентрация молекул.
Сумма молекулярных токов, охватываемых всем замкнутым контуром, равна:
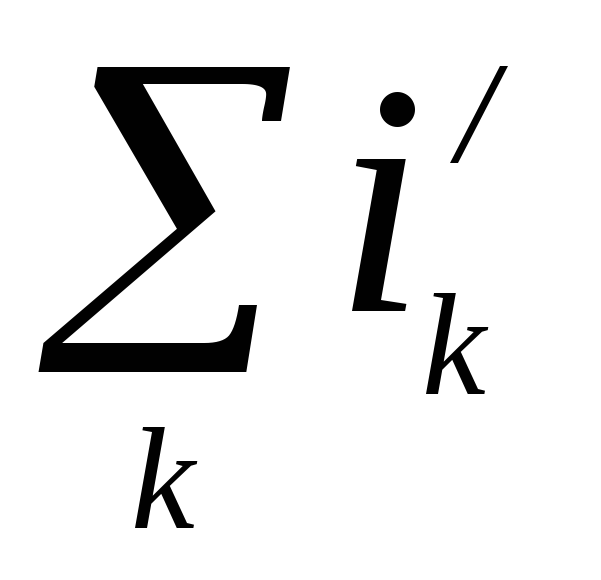
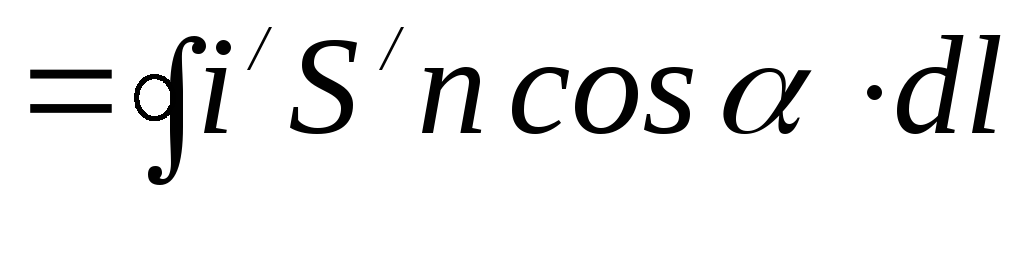. (5.8)
В этом выражении произведение 
равно магнитному моменту отдельной молекулы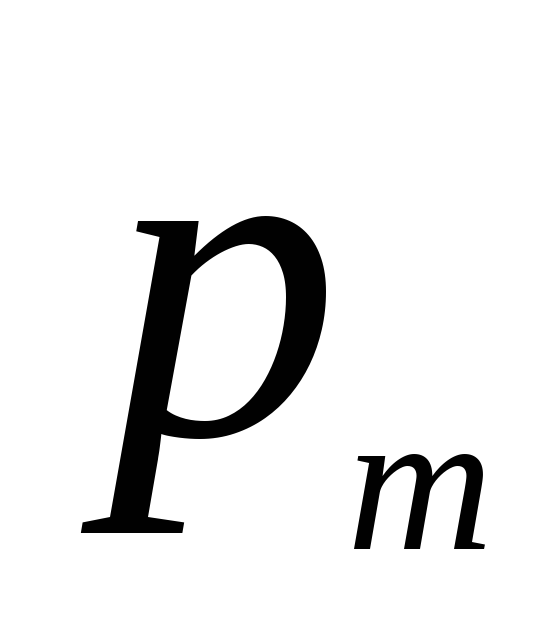
, а
– магнитному моменту единицы объема вещества или вектору намагниченности 
. Тогда
или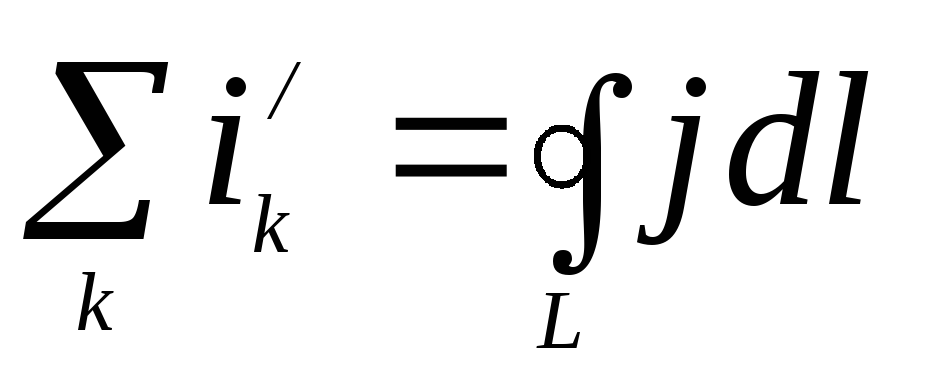 
. (5.9)
Подставим выражение (5.9) в формулу (5.5), получим:
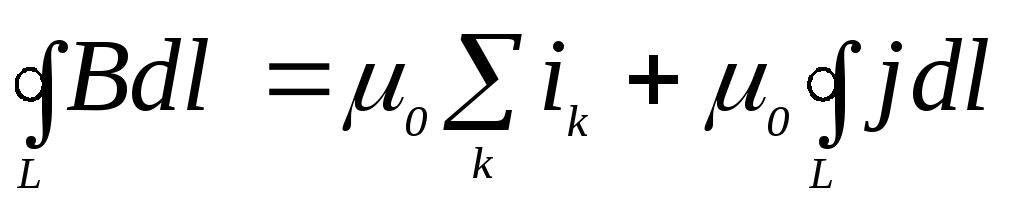. (5.10)
Перенесем интеграл из правой части формулы (5.10 в левую, и разделим все выражение на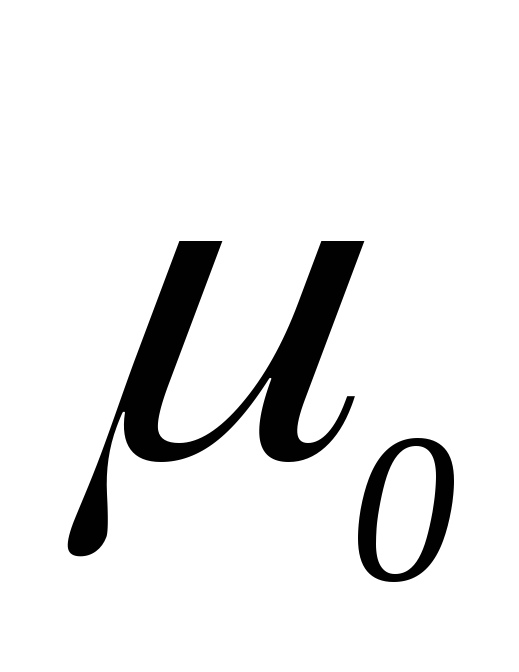 
:
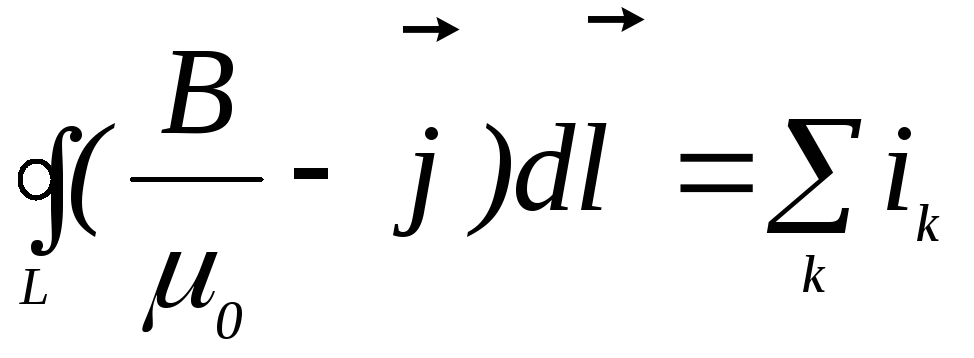. (5.11)
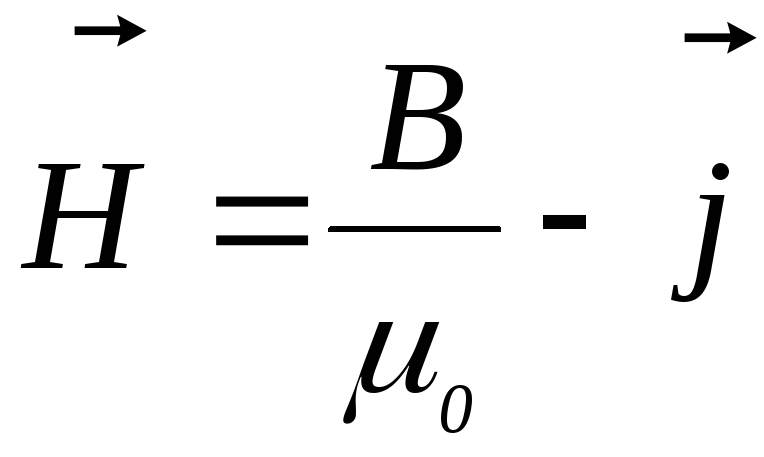. (5.12)
Вектор 
называетсянапряжённостью магнитного поля.Учитывая обозначение (5.12), формулу (5.11) можно записать в виде:
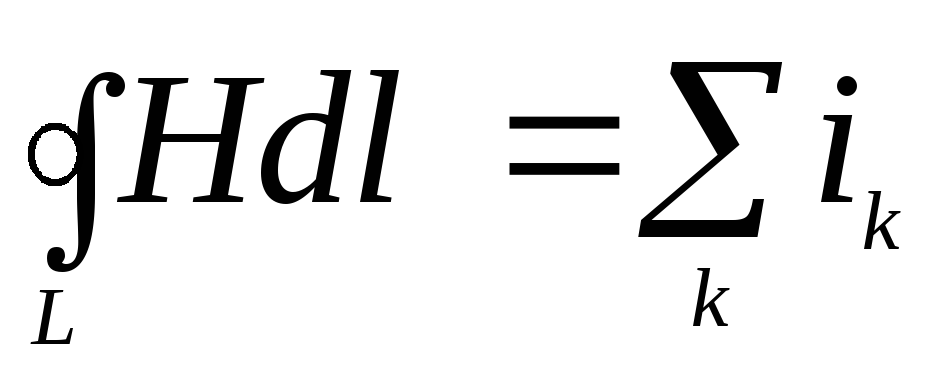. (5.13)
Выражение (5.13) называется законом полного тока для магнитного поля в веществе. Циркуляция вектора напряженности по произвольному замкнутому контуру равна произведению магнитной постоянной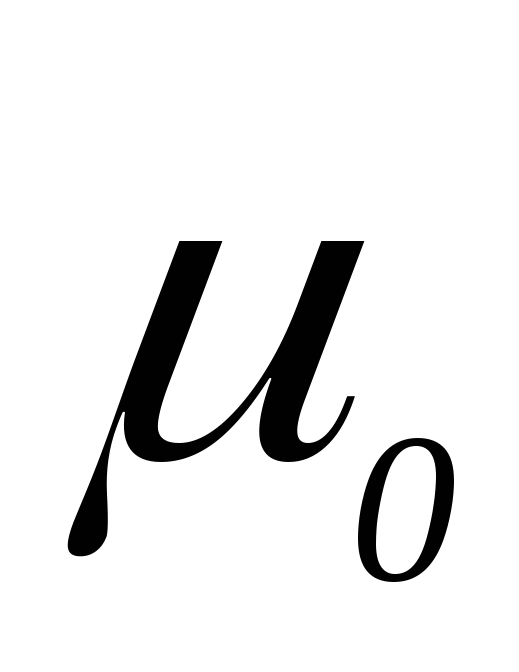 
на алгебраическую сумму токов проводимости, охватываемых этим контуром.
Примечание. Из формул (5.12) и (5.13) следует:
напряженность магнитного поля и намагниченность имеют одинаковую размерность;
напряженность характеризует магнитное поле, создаваемое токами проводимости.
5.3. Магнитные моменты электронов и атомов
Магнитные свойства вещества, в конечном счете, обусловлены магнитными свойствами составляющих его частиц. Исследования показали, что магнитные моменты протонов и нейтронов малы по сравнению с магнитными моментами электронов. Следовательно, магнитные свойства атома целиком определяются электронами.
Всякий атом можно рассматривать как динамическую систему, состоящую из ядра и движущихся вокруг его электронов.
Будем считать, что электроны в атомах движутся по круговым орбитам. Движение электрона по замкнутой орбите представляет собой ток. Направление тока противоположно движению электрона (рис.5.4).
Пусть 
– угловая скорость вращения электрона. Вектор угловой скорости образует с направлением движения электрона правовинтовую систему.
Величина орбитального тока равна
. (5.14)
Ему соответствует орбитальный магнитный момент электрона
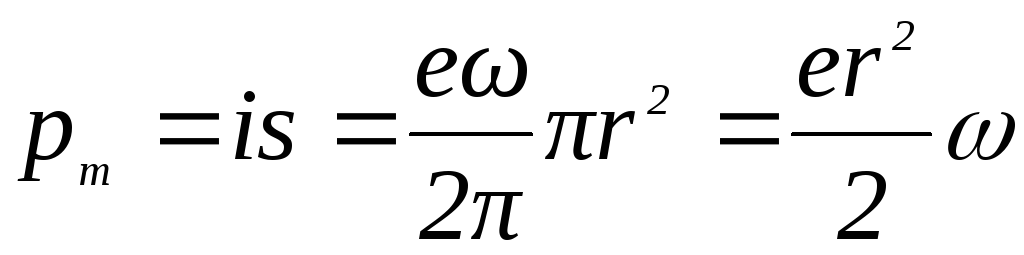. (5.15)
Магнитный момент образует с создающим его током правовинтовую систему и направлен противоположно вектору угловой скорости:
, 
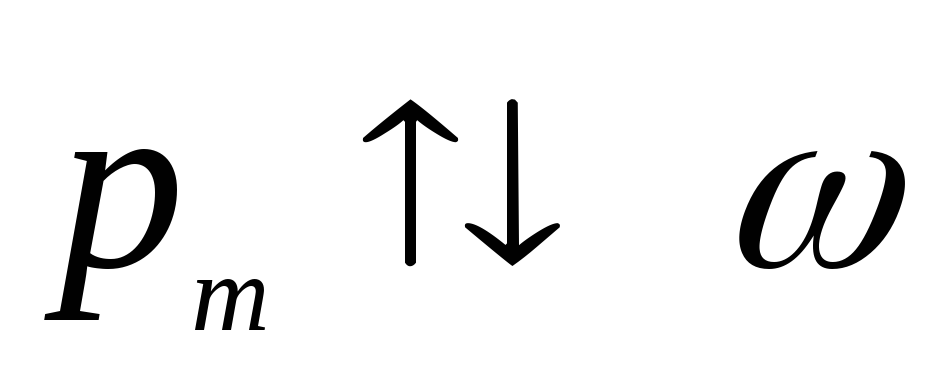. (5.16)
Полным током называют алгебраическую сумму токов, пронизывающих поверхность, ограниченную замкнутым контуром.
Приняв произвольно выбранное направление обхода какого-либо контура в магнитном поле за положительное, будем считать токи, пронизывающие этот контур, положительными, если их направление совпадает с направлением поступательного движения буравчика, рукоятка которого вращается в положительном направлении обхода контура.
Например, на рис. 1 ток I1— положительный, а ток I2 —
отрицательный. Полный ток, пронизывающий контур,
Рис 1. Токи, пронизывающие поверхность, ограниченную контуром
Рис 2. Напряженность магнитного поля провода с током
Магнитная индукция и напряженность поля в отдельных точках, расположенных на контуре, могут иметь или различные или одинаковые значения Допустим, что в точке а вектор индукции и пропорциональный ему вектор напряженности поля образует с элементом длины контура dl угол α. При этом HL = H cosα будет представлять собой касательную к контуру составляющую вектора напряженности магнитного поля. Магнитное напряжение HLdl на элементарном участке контура dl положительно, если направление вектора НL совпадает c выбранным направлением обхода контура, в противном случае оно будет отрицательным.
По закону полного тока МДС F вдоль контура равна полному току, который проходит сквозь поверхность ограниченную этим контуром, т. е.
Если контур совпадает с магнитной линией, то направление вектора напряженности поля совпадает с касательной к контуру и, следовательно, HL=H.
Если, кроме того, индукция B и напряжённость поля H во всех точках контура одинаковы, как вследствие симметрии при обходе вдоль контура рис. 5.17, то в формуле (5 23
напряженность можно вынести за знак суммирования и написать:
где знак обозначает сумму элементарных длин замкнутого контура, т. е. длину этого контура L; следовательно в этом случае
Выражение иногда называют циркуляцией вектора напряженности магнитного поля по замкнутому контуру. В соответствии с этим изменяют и формулировку закона полного тока.