Закон ома в электротехнике

Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.

Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.

Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.

Формула закона Ома записывается в следующем виде:

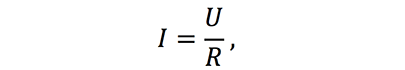
U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];

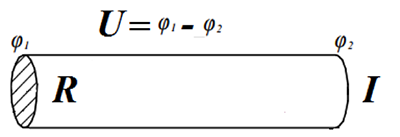
Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза

И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.

Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:

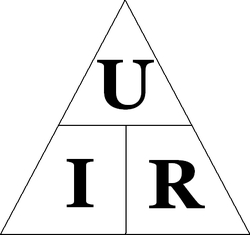
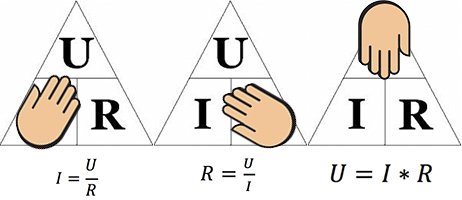
Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.

Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.

Где и когда можно применять закон Ома?

Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).

Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.

Значение Закона Ома

Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.

Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.

Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.

Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:

Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

См. также: Портал:Физика

Зако́н О́ма — эмпирический физический закон, определяющий связь электродвижущей силы источника (или электрического напряжения) с силой тока, протекающего в проводнике, и сопротивлением проводника. Установлен Георгом Омом в 1826 году (опубликован в 1827 году) и назван в его честь.

В своей работе [1] Ом записал закон в следующем виде:

X = a b + l , ( 1 ) <displaystyle X!=>,qquad (1)>

• X — показания гальванометра (в современных обозначениях, сила тока I );
• a — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока (в современной терминологии, электродвижущая сила (ЭДС) ε );
• l — величина, определяемая длиной соединяющих проводов (в современных представлениях соответствует сопротивлению внешней цепи R );
• b — параметр, характеризующий свойства всей электрической установки (в современных представлениях, параметр, в котором можно усмотреть учёт внутреннего сопротивления источника тока r ).

Формула (1) при использовании современных терминов выражает закон Ома для полной цепи:

I = ε R + r , ( 2 ) <displaystyle I!=<varepsilon ! over >,qquad (2)>

• ε <displaystyle <varepsilon !>>— ЭДСисточника напряжения, В;
• I <displaystyle I>— сила тока в цепи, А;
• R <displaystyle R>— сопротивление всех внешних элементов цепи, Ом;
• r <displaystyle r>— внутреннее сопротивление источника напряжения, Ом.

Из закона Ома для полной цепи вытекают следующие следствия:

• при r ≪ R <displaystyle rll R>сила тока в цепи обратно пропорциональна её сопротивлению, а сам источник в ряде случаев может быть назван источником напряжения;
• при r ≫ R <displaystyle rgg R>сила тока не зависит от свойств внешней цепи (от величины нагрузки), и источник может быть назван источником тока.

U = I R , ( 3 ) <displaystyle U!=IR,qquad (3)>

где U <displaystyle U> есть напряжение, или падение напряжения (или, что то же, разность потенциалов между началом и концом участка проводника), тоже называют «законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

ε = I r + I R = U ( r ) + U ( R ) . ( 4 ) <displaystyle <varepsilon !>=Ir+IR=U(r)+U(R).qquad (4)>

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

I = U R ( 5 ) <displaystyle I!=qquad (5)>

применима другая формулировка:

Выражение (5) можно переписать в виде

I = U G , ( 6 ) <displaystyle I!=,qquad (6)>

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный ом» — Mо [3] , в Международной системе единиц (СИ) единицей измерения проводимости является си́менс (русское обозначение: См; международное: S), величина которого равна обратному ому.

Содержание

Мнемоническая диаграмма для закона Ома

В соответствии с этой диаграммой формально может быть записано выражение:

R = U I , ( 7 ) <displaystyle R!=,qquad (7)>

которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

R = ϱ l s , ( 8 ) <displaystyle R!=<varrho l over s>,qquad (8)>

Закон Ома и ЛЭП

Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами, задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока P <displaystyle P> = ε I <displaystyle <varepsilon !I!>> при минимальных потерях мощности в линии передачи P ( r ) = U I , <displaystyle P(r)=UI,> где U = I r , <displaystyle U!=Ir,> причём r <displaystyle r> на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением

P ( r ) = P 2 r ε 2 . ( 9 ) <displaystyle P(r)=<frac <2>r><varepsilon ^<2>>>.qquad (9)>

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное увеличение ЭДС. Однако ЭДС ограничивается электрической прочностью обмотки генератора, поэтому повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в линии возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

Закон Ома в дифференциальной форме

Сопротивление R <displaystyle R> зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

J = σ E , <displaystyle mathbf =sigma mathbf ,>

• J <displaystyle mathbf >— вектор плотности тока,
• σ <displaystyle sigma >— удельная проводимость,
• E <displaystyle mathbf >— вектор напряжённости электрического поля.

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость σ i j <displaystyle sigma _> является симметричным тензором ранга (1, 1), а закон Ома, записанный в дифференциальной форме, приобретает вид

J i = ∑ i = 1 3 σ i j E j . <displaystyle J_=sum _^<3>sigma _E_.>

Раздел физики, изучающий течение электрического тока (и другие электромагнитные явления) в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновременности достижения напряжением и током своих максимальных значений, то есть учёт фазового сдвига.

Если ток является синусоидальным с циклической частотой ω , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

U = I ⋅ Z , <displaystyle mathbb =mathbb cdot mathbb ,>

• U = U 0 e i ω t <displaystyle mathbb =U_<0>e^>— комплексное напряжение или разность потенциалов,
• I <displaystyle mathbb >— комплексная сила тока,
• Z = R e − i δ <displaystyle mathbb =Re^<-idelta >>— комплексное сопротивление (электрический импеданс),
• R = √R_a 2 + R_r 2 — полное сопротивление (модуль импеданса),
• R_r = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ = − arctg (R_r/R_a) — сдвиг фаз между напряжением и силой тока (фаза импеданса, с точностью до обратного знака).

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, U = U 0 sin ⁡ ( ω t + φ ) <displaystyle U=U_<0>sin(omega t+varphi )> подбором такой U = U 0 e i ( ω t + φ ) , <displaystyle mathbb =U_<0>e^,> что Im ⁡ U = U . <displaystyle operatorname mathbb =U.> Тогда все значения токов и напряжений в схеме надо считать как F = Im ⁡ F . <displaystyle F=operatorname mathbb .>

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Нелинейность цепи приводит к возникновению гармоник (колебаний с частотой, кратной частоте тока, действующего на цепь), а также колебаний с суммарными и разностными частотами. Вследствие этого закон Ома в нелинейных цепях, вообще говоря, не выполняется.

Трактовка и пределы применимости закона Ома

Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций.

В классическом приближении закон Ома можно вывести при помощи теории Друде:

J = n ⋅ e 0 2 ⋅ τ m ⋅ E = σ ⋅ E . <displaystyle mathbf =<frac <0>^<2>cdot au >>cdot mathbf =sigma cdot mathbf .>

• σ <displaystyle sigma >— электрическая удельная проводимость;
• n <displaystyle n>— концентрация электронов;
• e 0 <displaystyle e_<0>>— элементарный заряд;
• τ <displaystyle au >— время релаксации по импульсам (время, за которое электрон «забывает» о том, в какую сторону двигался);
• m <displaystyle m>— эффективная масса электрона.

Проводники и элементы, для которых соблюдается закон Ома, называются омическими.

Закон Ома может не соблюдаться:

• При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
• При низких температурах для веществ, обладающих сверхпроводимостью.
• При заметном нагреве проводника проходящим током, в результате чего зависимость напряжения от тока (вольт-амперная характеристика) приобретает нелинейный характер. Классическим примером такого элемента является лампа накаливания.
• При приложении к проводнику или диэлектрику (например, воздуху или изоляционной оболочке) высокого напряжения, вследствие чего возникает пробой.
• В вакуумных и газонаполненных электронных лампах (в том числе люминесцентных).
• В гетерогенных полупроводниках и полупроводниковых приборах, имеющих p-n-переходы, например, в диодах и транзисторах.
• В контактах металл-диэлектрик (вследствие образования пространственного заряда в диэлектрике) [4] .

Электротехника. Основы. Закон Ома

В электротехнике, как и в любой другой науке, существуют базовые понятия, без понимания которых не удастся овладеть этой областью знаний. Здесь такими понятиями являются электрическое напряжение, электрический ток и электрическое сопротивление.

Закон Ома

Закон Ома был открыт в результате экспериментов Георга Ома с гальванометром и простой электрической цепью из источника ЭДС и сопротивления. Со временем формула полученная Омом претерпела несколько изменений.

Закон Ома для участка цепи без ЭДС

Может быть сформулирован через сопротивление [1, стр.33][2, стр.15]:

• I – ток через участок ab электрической цепи;
• U_ab – напряжение на участке ab электрической цепи;
• R – сопротивление участка ab электрической цепи.

Или через проводимость:

• G – проводимость участка ab электрической цепи.

Формула (1, 2) справедлива для электрической цепи представленной ниже на рисунке 1.

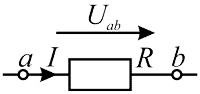
Рисунок 1 – Участок цепи без ЭДС

Закон Ома для участка цепи содержащего ЭДС

Или обобщённый закон Ома. Формулируется следующим образом [1, стр.34][2, стр.17]:

• I – ток через участок ac электрической цепи;
• U_ab – напряжение на участке ab электрической цепи;
• E – ЭДС на участке bс электрической цепи;
• R – сопротивление участка ab электрической цепи.

Или через проводимость:

• G – проводимость участка ab электрической цепи.

Формула (3, 4) справедлива для электрической цепи представленной ниже на рисунке 2.

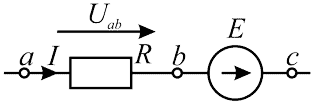
Рисунок 2 – Участок цепи содержащий ЭДС

Закон Ома для полной цепи

Закон формулируется следующим образом [1, стр.34][2, стр.17]:

• I – ток в электрической цепи;
• E – ЭДС электрической цепи;
• R – сопротивление электрической цепи;
• r – внутреннее сопротивление источника ЭДС.

Формулировка выражения (5) через проводимость неудобна и здесь приведена не будет. Ниже на рисунке 3 изображена схема электрической цепи для которой справедливо выражение (5).

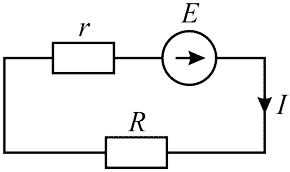
Рисунок 3 – Полная цепь

На схеме видно, что R и r соединены последовательно, а в формуле это отражено как сумма R (сопротивления цепи) и r (внутреннего сопротивления источника ЭДС). Заменим выражение R + r на R_п

• R_п – полное сопротивление электрической цепи (включая сопротивление источника ЭДС).

Закон Ома в дифференциальной форме

Закон Ома в дифференциальной форме, представленный в выражении (7), справедлив для неоднородного, но изотропного вещества [3].

• (vecjmath) – плотность тока;
• ρ – удельное сопротивление;
• (vec E) – напряжённость электрического поля.

Примеры применения

Ниже приведены несколько примеров для демонстрации применения разных формулировок закона Ома.

Пример 1

Схема задания приведена на рисунке 4. На схеме R = 5,2 Ом, U = 26 В. Определить I.

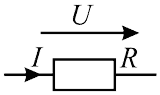
Рисунок 4 – Схема к 1 и 2-му примеру

Для решения задания воспользуемся выражением (1):

Пример 2

Схема задания приведена на рисунке 4. К данному участку цепи приложено напряжение 24 В и по нему протекает ток 1,5 А. Определить проводимость участка цепи.

Для решения задания преобразуем выражение (2) относительно G:

Пример 3

Схема задания приведена на рисунке 5. На схеме U = 220 В, I = 0,5 А, R = 140 Ом. Определить E.

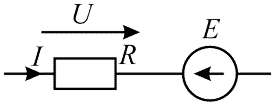
Рисунок 5 – Схема к 3-му примеру

Для решения задания преобразуем выражение (3) относительно E:

Подставим в выражение (10) известные величины:

Пример 4

Сопротивление электрической цепи, приведенной на рисунке 3 составляет 12 Ом, напряжение источника ЭДС включенного в цепь – 9 В. Измерения показали, что по цепи протекает ток 0,72 А. Необходимо определить внутреннее сопротивление источника ЭДС.

Преобразуем выражение (5) относительно r:

Определим внутренней сопротивление источника ЭДС, подставив в выражение (10) известные величины:

Использованные термины

Электрический потенциал точки:

Физическая величина, равная потенциальной энергии, которой обладает элементарный положительный заряд, помещенный в электрическое поле.

Потенциал обозначается буквой φ греческого алфавита и измеряется в вольтах (В). Он не имеет направления и записывается как скаляр.

Физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из точки А в точку Б электромагнитного поля, определяемая как разность потенциалов этих точек: U_ab = φ_a – φ_b.

Напряжение обозначается буквой U (u) латинского алфавита и измеряется в вольтах (В). Напряжение – скалярная величина, но на электрических схемах указывают его положительное направление.

Электродвижущая сила (ЭДС):

Также как и напряжение это физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из одной точки электромагнитного поля в другую.

ЭДС обозначается буквой E (e) латинского алфавита и измеряется в вольтах (В). ЭДС – скалярная величина, но на электрических схемах указывают её положительное направление. Она численно равна напряжению на зажимах не подключенного источника.

Физическая величина, равная количеству заряженных частиц прошедших через поперечное сечение проводника за единицу времени. Как явление – направленное движение заряженных частиц.

Напряжение обозначается буквой I (i) латинского алфавита и измеряется в амперах (А). Ток, так же как и напряжение, величина скалярная, и на электрических схемах тоже указывают его положительное направление [2, стр.11] .

Физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади.

Плотность тока обозначается буквой (vecjmath) латинского алфавита и измеряется в амперах на метр квадратный (А/м 2 ). Плотность тока – векторная величина [4].

Физическая величина, характеризующая способность проводника препятствовать прохождению по нему тока.

Сопротивление обозначается буквами R (r), X (x) или Z (z) латинского алфавита (последние два обозначения применяются для реактивного и комплексного сопротивления соответственно) и измеряется в омах (Ом). Как и предыдущие, сопротивление – скалярная величина.

Физическая величина, характеризующая насколько хорошо проводник проводит электрический ток, является обратной сопротивлению: G = 1/R.

Проводимость обозначается буквами G (g) латинского алфавита и измеряется в сименсах (См). Так же как и сопротивление проводимость – скалярная величина.

Физическая величина, численно равная сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м 2 .

Удельная проводимость обозначается буквами ρ греческого алфавита и измеряется в омах на метр (Ом×м). Является скалярной величиной. [3].

В дальнейшем при использовании вышеперечисленных терминов слово "электрический" будет упускаться.