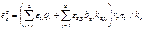В основу расчёта и моделирования естественного освещения зданий положены два закона.
Первый закон – проекции телесного угла. Он гласит, что освещённость Ем в какой-либо точке поверхности помещения, создаваемая равномерно светящейся поверхностью неба, прямо пропорциональна яркости неба и площади проекции на освещаемую поверхность телесного угла, под которым из данной точки виден участок неба (рисунок 3.1) [10].
| Окно |
Рисунок 3.1 – Схемы к закону проекции телесного угла
Для аналитического вывода этого закона примем два допущения: 1) освещаемая поверхность располагается в помещении горизонтально; 2) радиус полусферы принимается равным единице.
Проводим из точки М полусферу и обозначим её яркость через L. Определим освещённость в точке М, создаваемую весьма малым участком полусферы dS, который можно принять за точечный источник света.
Силы света элементарного участка dS, обладающего яркостью L, определяется по формуле
Элементарную освещённость точки М находим по формуле
ΔE = dJ cosα / R². (3.2)
Если выразить силу света dJ через яркость, то при радиусе полусферы равной единице (R=1), имеем
ΔЕ = L dS cosα, (3.3)
но dS cosα = dσ, т.е. площади проекции dS на освещаемую поверхность.
Интегрируя при равномерном распределении яркости участка небосвода, получим
т.е. освещённость в какой-либо точке помещения равна произведению яркости участка неба, видимой из данной точки через окно, на проекцию этого участка неба на освещаемую поверхность.
Представим теперь, что точка горизонтальной поверхности находится на открытом месте и освещается всей полусферой с равномерной распределённой яркостью. В этом случае
где πR² – площадь полусферы на горизонтальную поверхность,
но R=1, следовательно,
Критерием оценки естественного освещения служит коэффициент естественной освещённости (КЕО), который представляет собой отношение естественной освещённости, создаваемой в некоторой точке заданной плоскости внутри помещения светом неба (непосредственно или после отражения) Ем, к одновременному значению наружной горизонтальной освещённости под открытым полностью небосводом Ен. КЕО выражается в процентах. Участие прямого солнечного света в создании Ем и Ен исключается. Значение КЕО находится из выражения
Наряду с КЕО, в расчетах естественного освещения применяется геометрический коэффициент естественной освещенности ε, который представляет собой отношение освещенности, создаваемой в некоторой точке заданной плоскости внутри помещения светом, прошедшим через незастекленный световой проем, от равномерно яркого неба Ем к одновременному значению наружной горизонтальной освещенности под открытым полностью небосводом Ен. Участие прямого солнечного света в создании Ем и Ен исключается. Значение геометрического КЕО находится из выражения
Пользуясь выше названной формулой, имеем
ем = Lσ / Lπ = σ / π. (3.10)
Таким образом, значение КЕО в какой-либо точке поверхности определяется отношением проекции на освещаемую поверхность видимого из данной точки помещения участка неба к величине π (равной 3,14). Это отношение представляет геометрическое выражение коэффициента естественной освещенности.
Практическое значение этого закона очень велико: пользуясь им, можно определять относительную световую активность различных светопроемов и сравнивать освещенности, создаваемые одним и тем же светопроемом, расположенным различно относительно рабочей плоскости (рисунок 3.2).
 |
Рисунок 3.2 – Определение относительной световой активности
светопроёмов с помощью закона проекции телесного угла
при расположении точки на горизонтальной (а)
и вертикальной (б) плоскости
На основе этого закона разработаны графические способы расчёта естественного освещения (в частности, графики А.М. Данилюка), получившие широкое распространение в проектной и расчётной практике.
Второй закон– закон светотехнического подобия. Сущность этого закона уясняется из схемы на рисунке 3.3 [10].
| 1-1 |
Рисунок 3.3 – Схема к закону светотехнического подобия
Освещённость в точке М помещения создаётся через окна, обладающие яркостью L1,L2. Различная яркость может создаваться, например, применением различных сортов стекла (оконного, листового, контрастного, матированного и д.р.). Однако при различных размерах окон (I и II) освещённость в точке М создаётся одним и тем же телесным углом, вершина которого совпадает с точкой М.
Из закона проекции телесного угла следует, что освещённость в точке М остаётся постоянной при условии, что L1=L2=Ln=const. Следовательно, освещённость в какой-либо точке помещения зависит не от абсолютных, а от относительных размеров помещения.
Большое практическое значение этого закона заключается, прежде всего, в том, что он позволяет задачи естественного освещения решать, пользуясь методом моделирования, оценивая условия освещения помещений на моделях. При этом тщательно соблюдаются все геометрические и светотехнические параметры интерьера.
На основе этого закона создаются экспериментальные установки, называемые искусственным небом, широко применяемые при проведении различных светотехнических и архитектурного характера исследований на моделях зданий и сооружений. В нашей стране, в частности в Москве, существует крупнейший в Европе искусственный небосвод, где осуществляют теоретические и экспериментальные исследования по светотехнике. Пример расчёта естественного освещения помещений представлен ниже на рисунке 3.4.
Читайте также:
|
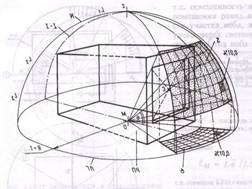
Вывод- освещенность в точке М, созд малым участком ∆S определяется по формуле Ем=У*cosα/r 2
Непостоянство в помещениях естественного освещения во времени вызвало необходимость ввести отвлеченную единицу измерения естественной освещенности, называемую КЕО